Exponential size
If ( 2 1 ) x > ( 2 1 ) y , which of the following must be true about x and y ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Thanks very helpful
=> 2 x 1 > 2 y 1 => 2 y > 2 x => y > x
Why does 2 y > 2 x imply that y > x ?
Log in to reply
It's logic
Log in to reply
It seems trivial, but can you give a rigorous proof?
Log in to reply
@Jesse Nieminen – Take log on both sides give,
ylog2>xlog2
log2 get cancelled
Therefore, y>x
Log in to reply
@Genis Dude – Why is taking logarithms justified? Why does it preserve the inequality as it is?
For example, multiplying both sides of the inequality by − 1 flips the inequality other way around.
Log in to reply
@Jesse Nieminen – If u multiply by negative number for example -1 , we will get log(-1) which is not defined.So we cannot cancel it
Log in to reply
@Genis Dude – Yes, but that does not explain why taking logarithms is justified.
Log in to reply
@Jesse Nieminen – We took log so that we will get the inequality btw x and y
Log in to reply
@Genis Dude – But why can we take logarithm of both side of the inequality and keep the inequality as it is?
Why does a > b imply that lo g 2 a > lo g 2 b ?
Log in to reply
@Jesse Nieminen – I did not said logx(base 2).I said xlog2<ylog2 Log2 is a constant value(0.301) So it get cancelled
Log in to reply
@Genis Dude – Don't refer me to a wiki. Yes, x lo g 2 < y lo g 2 ⟹ x < y is true, when the base of the logarithm is greater than 1 , but why is lo g 2 x < lo g 2 y ⟹ x lo g 2 < y lo g 2 true, when the base is greater than 1 ?
Give me a proof that taking logarithm (of base greater than one) of both sides of an inequality is allowed. Hint: Logaritmic functions (with base greater than 1 ) are strictly increasing functions.
Log in to reply
@Jesse Nieminen – log2^x=log(2 2 2. .. .)till x times log2+ log2+log2..... (till x times) xlog2
@Jesse Nieminen – Also taking log doesn't change the inequality
@Jesse Nieminen – https://brilliant.org/wiki/logarithmic-inequalities/
Also, I have a counterexample for you, ( − 1 ) 2 > ( − 1 ) 3 is true, but 2 > 3 is false.
Define F ( a ) = x a for 0 < x < 1 , then F ′ ( a ) = x a ln x < 0 which is obvious since 0 < x < 1 . So F is decreasing and thus if ( 2 1 ) x > ( 2 1 ) y which implies x < y .
if y > x then y = x + z and z > 0.
0 < ( 1 / 2 ) z < 1 for z > 0 .
( 1 / 2 ) y = ( 1 / 2 ) x + z = ( 1 / 2 ) x ( 1 / 2 ) z
It follows that ( 1 / 2 ) x > ( 1 / 2 ) x ( 1 / 2 ) z = ( 1 / 2 ) y
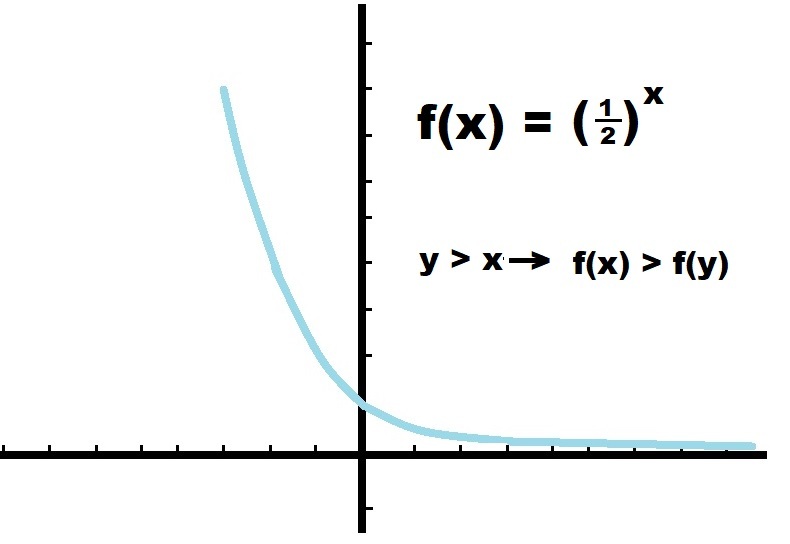
0.5 * 0.5 = 0.25. 0.25 < 0.5. Thus, adding powers to 0.5 makes it smaller.
Guys it is simple 2^(-x)>2^(-y) -x>-y x<y(from inequalities) Hope it helps
Why does 2 − x > 2 − y imply that − x > − y ?
Log in to reply
It's logic
Log in to reply
It seems trivial, but can you give a rigorous proof?
between 0-1, if we give power in any number it will decrease.
so, easily ,0.5 * 0.5 = 0.25.
0.25 < 0.5.
Thus, adding powers to 0.5 makes it smaller.