Exponentials

Calculus Level 2

$\huge x^{x^{x^{\cdot^{\cdot^\cdot}}}}=3$

Find the value of $x$ that satisfies the infinitely nested function above.

Give your answer to 3 decimal places.

If you come to the conclusion that no such real number $x$ exists, enter 666.

The answer is 666.

1 solution

Otto Bretscher
Feb 12, 2016

If we assume that the given equation has a solution $x$ , then $x^3=3$ so $x=\sqrt[3]{3}\approx 1.44$ . We need to examine whether the infinite power tower $x^{x^{x^{.^{.^.}}}}$ with $x=\sqrt[3]{3}$ actually attains the value 3.

The value of the power tower is defined as the limit of the sequence given by $x_0=\sqrt[3]{3}$ and $x_{n+1}=(\sqrt[3]{3})^{x_n}=3^{x_n/3}$ . If we define $f(x)=3^{x/3}$ , an exponential growth function, we can write $x_{n+1}=f(x_n)$ . The function $f(x)$ has two equilibrium points, where $f(x)=x$ , namely, $a=-\frac{W(-\ln\sqrt[3]{3})}{\ln\sqrt[3]{3}}\approx 2.478$ and $b=3$ .

If $x_n<a$ then $f(x_n)<f(a)$ so $x_{n+1}<a$ . Since $x_0=\sqrt[3]{3}<a$ , this shows that the sequence $x_n$ is bounded by $a$ . Thus the sequence will not converge to $b=3$ .

Since the infinite power tower $x^{x^{x^{.^{.^.}}}}$ with $x=\sqrt[3]{3}$ does not attain the value 3, the given equation has no real solution $x$ . The answer is $\boxed{666}$

The answer should be changed. The answer x is valid only if x<=e^(1/e), Lambert W-Function

Mardokay Mosazghi - 5 years, 4 months ago

yes,

i don't know why 145 people solved it and no one changed the answer

Hamza A - 5 years, 4 months ago

They "solved" it wrong ;)

Otto Bretscher - 5 years, 4 months ago

@Otto Bretscher – most of them r level 2 to 3 in calculus,so they probably won't notice :)

but i don't know how @Jerry Han Jia Tao didn't notice

Hamza A - 5 years, 4 months ago

@Hamza A – This "nested" stuff is taught wrong at many schools around the world

Otto Bretscher - 5 years, 4 months ago

@Otto Bretscher – that is,if they are even taught.

i'm taking algebra 1 now because that's all what my school can offer me,and it's not even advanced,just linear equations and parabolas and a bunch of other stuff

Hamza A - 5 years, 4 months ago

@Otto Bretscher – they almost never teach you beautiful math,just that old, dry ,ugly math as G.H. Hardy described it in schools.I'm really happy i found a site like brilliant with people that feel like me :)and,of course,beautiful math ;)

Hamza A - 5 years, 4 months ago

@Hamza A – I like the advice they give at the "Russian School of Mathematics", in the best Soviet tradition: "Forget the rules! Just think!" Sadly, most school around the world teach just the opposite...

Otto Bretscher - 5 years, 4 months ago

@Otto Bretscher – Sir,can you please try my problem named "Global maxima of f(x)".Please post solution if you get the answer.Thanks.

Indraneel Mukhopadhyaya - 5 years, 4 months ago

@Hamza A – I am not too familiar with calculus actually.

A Former Brilliant Member - 5 years, 4 months ago

@A Former Brilliant Member – As you can see from my solution, there is no calculus required here except for the simple notion of the limit of a sequence.

Otto Bretscher - 5 years, 4 months ago

Sir,can you please attempt my problem named "Global maxima of f(x)".Please post the solution if you get the correct answer.I am unable to solve the question myself.Thanks.

Indraneel Mukhopadhyaya - 5 years, 4 months ago

This problem does not look like a lot of fun to me... I don't think I want to tackle this on Valentine's day ;) It's a second order homogeneous linear differential equation... those tend to be messy and highly technical to solve. We have some talented people on this site who seem to enjoy this kind of stuff, like @Brian Charlesworth and @Mark Hennings ... I'm sure they will be glad to help.

Otto Bretscher - 5 years, 4 months ago

Can you please check that you entered the question correctly? My initial analysis (admittedly much of it numeric) has the function that satisfies the differential equation $f''(x) +x|\sin x| f'(x) + f(x) = 0$ with $f(0) = -3$ and $f'(x) = 4$ having a non-integer maximum of about $2.73197$ .

Mark Hennings - 5 years, 4 months ago

I have re-checked the question,everything is correctly given,also the answer comes out to be positive integer,how have you managed to solve that differential equation?Now I am going to bed as it is 11 pm right now in India.I will try the problem again tomorrow morning.

Indraneel Mukhopadhyaya - 5 years, 4 months ago

I got you bro!!

Mardokay Mosazghi - 5 years, 4 months ago

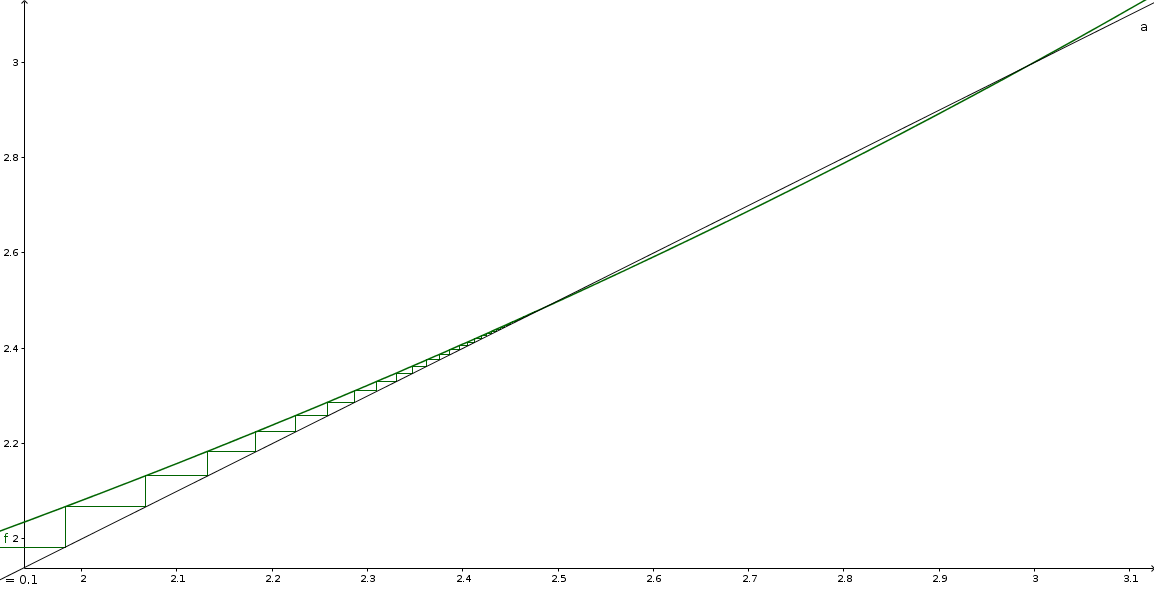The sequence is "absorbed" before it evolves to 3

Larger Version

@Otto Bretscher

Agnishom Chattopadhyay - 5 years, 3 months ago

How would we determine the equilibrium points ? I am unable to understand that sir. Even I just want to know what do we mean by equilibrium points in this case ?

$e^{xln(3)^{\frac{1}{3}}} = x\implies -xln(3)^{\frac{1}{3}}e^{-xln(3)^{\frac{1}{3}}}=-ln(3)^{\frac{1}{3}}$

$W(-xln(3)^{\frac{1}{3}}e^{-xln(3)^{\frac{1}{3}}})=W(-ln(3)^{\frac{1}{3}}) = W(-ln(3)^{\frac{1}{3}})$

$x=-\frac{ W(-ln(3)^{\frac{1}{3}})}{ln(3)^{\frac{1}{3}}}$ So computing the lambert function we get two values namely $-1.096586$ & $-0.909259$ . If we choose the first one it's $2.99\approx 3$ but choosing the latter we get what you showed above. So why we have neglected the first value.

And for the bounding part if we observe that $x_0<a$ , So that implies It's not converging to the equilibrium point $b=3$ . @Otto Bretscher Sir, I will be glad if you look into my queries.

Aditya Narayan Sharma - 5 years, 1 month ago

Let me try to answer your questions one by one as I find time.

First of all, a fixed point of a function $f$ is simply a point $x$ where $f(x)=x$ .

In our example, we are looking for the points $x$ where $3^{x/3}=x$ . We don't necessarily have to "find" them (their exact values), but we have to "understand them": How many are there and on what intervals are they located. We know, by construction, that $b=3$ is one fixed point; it is unstable , though, since $f'(3)>1$ . There must be one other fixed point $a<3$ ; in fact, $a$ is on the interval $(2,3)$ since $f(2)>2.$ This information is enough to solve our problem.

It is possible to express the exact values of the fixed points in terms of the Lambert $W$ function, as I show in my solution. If we use the principal branch $W(x)=W_0(x)$ of the Lambert Function (as we do for square roots or logarithms, for example), we find $a=-\frac{W(-\ln\sqrt[3]{3})}{\ln\sqrt[3]{3}}\approx 2.478$ . The other real branch, $W_{-1}(x)$ , would give us the solution $3$ , as you point out.

I'm not sure whether there is a question contained in your last paragraph, "And for the bounding part...".

PS: As I read my solution again, I noticed a typo, a missing negative sign... corrected

Otto Bretscher - 5 years, 1 month ago

Thank you sir @Otto Bretscher for this brief explanation , Now I understand that the principal branch of Lambert's function must be taken into account so as to get the correct answer. Thanks for your time !

Aditya Narayan Sharma - 5 years, 1 month ago

Hey Jerry, just want to say that I solved this without cheating, but I found out that there were no "decimals OK" beneath the answer box. Better fix the answer :)

Steven Jim - 4 years, 2 months ago

Exponentials

The answer is 666.

1 solution

1 pending report

Vote up reports you agree with