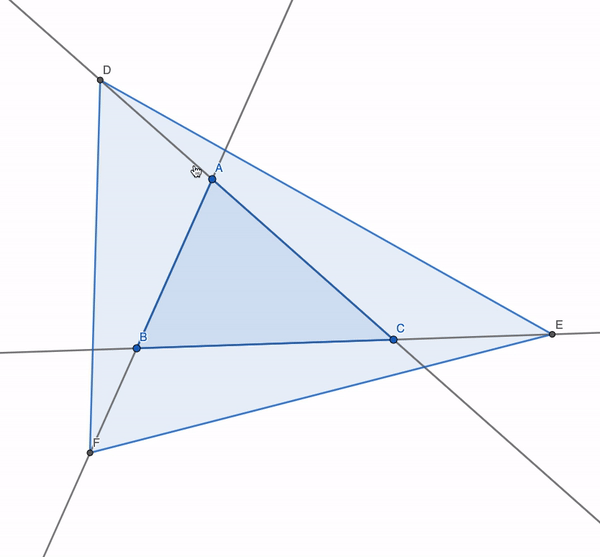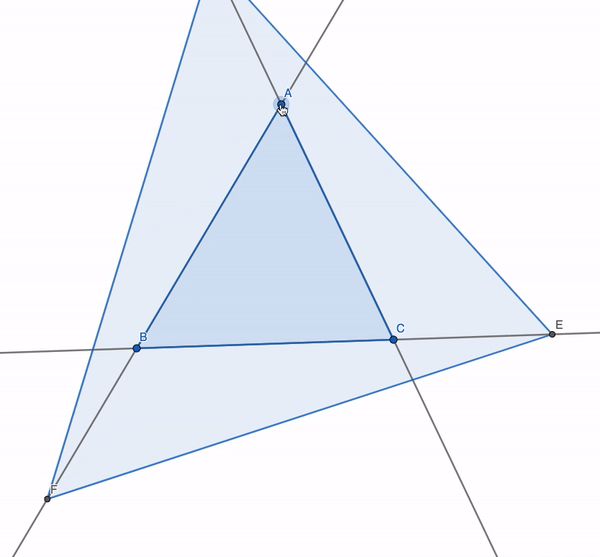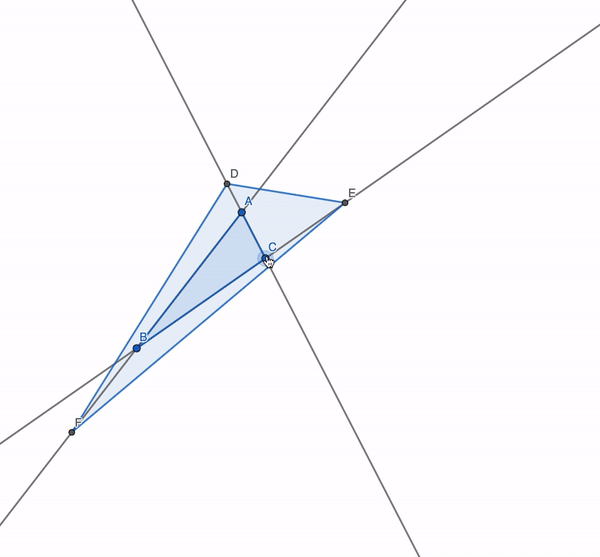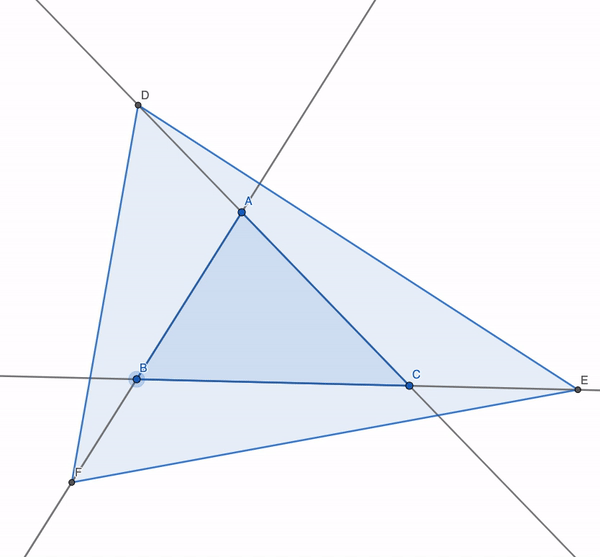
Extended Golden Triangle
The sides of △ A B C are extended so that B is between A and D , C is between B and E , A is between C and F , and A B A D = B C B E = C A C F = ϕ = 2 1 + 5 .
Find the ratio of the area of △ D E F to the area of △ A B C .
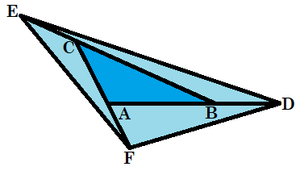
The answer is 4.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
This week's CEMC POTW instantly reminded me of this problem.
Labelling a = B C , b = C A , c = A B , we have A D = φ c and A F = ( φ − 1 ) b . Hence Area Δ A F D = 2 1 φ ( φ − 1 ) b c sin A = φ ( φ − 1 ) × Area Δ A B C
Since by definition, φ ( φ − 1 ) = 1 , the areas of the four triangles Δ A B C , Δ A F D , Δ B D E , Δ C E F are all the same; so the area of Δ D E F is 4 times the area of Δ A B C .
Nice solution!
Yes, very clean solution (upvoted)! I really want to visualise this. It's a super neat problem.
It would be awesome if we are somehow able to geometrically and intuitively show that each of the three extended areas are equal!!!
Log in to reply
I don't think it is what you are looking for, but I posted another approach that may inspire you to think about the problem differently.
Log in to reply
A visual proof would be fantastic. It seems there are two things to prove: first, that the three surrounding triangles all have the same area; second, that the golden ratio makes them equal the first triangle.
I've just realised another way of proving the first part: the base B D of Δ B D E is φ − 1 times the base A B of Δ A B C . The height of Δ B D E is φ times the height of Δ A B C ; so again we get Δ B D E = φ Δ A B C . This might be a bit easier to show visually than the formula involving angles.
The absolute nicest way would probably be with a dissection proof; but here you'd have to incorporate the fact that φ ( φ − 1 ) = 1 somehow.
One "natural habitat" of φ is in regular pentagons/pentagrams - the ratios between sides, diagonals and the segments formed by the intersections of diagonals can all be written in terms of the golden ratio. As per @David Vreken 's solution, if you prove it for any particular triangle, it's proved for all triangles; perhaps one of the triangles related to a regular pentagon would work?
Log in to reply
@Chris Lewis – Or how about a Kepler triangle ?
@Chris Lewis – For now, I am just able to map out any triangle and play with it. Nothing so special. I thought something might click, but it hasn't yet...
Try my vector-based solution...
Note that B E = φ B C and B D = ( φ − 1 ) A B , so that B D × B E = φ ( φ − 1 ) B C × B A = B C × B A and hence triangles A B C and B D E have the same area. SImilarly, A F D and C E F have the same area as well, and hence the ratio between the areas of D E F and A B C is 4 .
Why does proving B D × B E = B C × B A , show that triangles have the same area. I haven't yet studied vector multiplication...
Log in to reply
The vector product of two vectors is a vector normal to both, of magnitude equal to the product of their moduli with the sine of the angle between them. The modulus of the vector product is thus twice the area of the triangle formed by the two vectors.
△ A B C can be stretched and skewed to an equilateral triangle with a side length of 1 and still preserve the ratio of areas:
Using the law of cosines on △ A D F , D F = ϕ 2 + ( ϕ − 1 ) 2 − 2 ⋅ ϕ ⋅ ( ϕ − 1 ) ⋅ cos 1 2 0 ° = 2 , and by symmetry △ D E F is also an equilateral triangle.
Since the ratio of sides of the two equilateral triangles is 1 2 , the ratio of their areas is 1 2 2 2 = 4 .