Extension extended
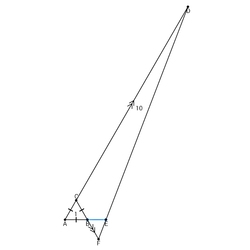 Δ
ABC
is an equilateral triangle with side length 1.
AC, CB
&
AB
are extended respectively to
D, F
&
E
such that
E
is a point on segment
DF
.
Δ
ABC
is an equilateral triangle with side length 1.
AC, CB
&
AB
are extended respectively to
D, F
&
E
such that
E
is a point on segment
DF
.
Given that, lengths: CD = 1 0 , BF = 1 .
If the length of segment BE can be expressed as b a where a & b are coprime positive integers, then find a + b .
The answer is 11.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Use Menelaus' Theorem for a one-line solution.
Log in to reply
Thanks, didn't know that before.
Then also, you'll have to find D F E F
You mean to use Menelaus' Theorem like this right?
A C D C × A B B E × D F E F = 1
Log in to reply
No, that exact approach was not how I intended to use it. They are many ways of using it, especially with the numerous number of triangles and transversals that are present in the setup. For example, taking triangle A B C with transversal E D F , we get that
1 = D C A D × F B C F × E A B E
This tells us
1 = 1 0 1 1 × 1 2 × B E + 1 B E
Hence, B E = 2 2 − 1 0 1 0 and we are done.
If you want to use D F E D (which is currently another unknown), then you will need to use additional triangle-transveral pairs like triangle CDF with transversal ABE, to eliminate it.
Log in to reply
@Calvin Lin – Oh! Yes, that's simple! Thanks!
@Calvin Lin sir, do you like Menelaus' Theorem so much?!
Let's take a look at the very familiar parallel line dividing system of a segment.
Segment AB is divided into 2, 3 & 4 equal parts by the Black , Cyan , & Red lines respectively.
Similarly, in this problem if we extend BE to BG where BG = 1 & draw a ray GF , then we can get the answer very easily. Here is a picture:
Notice that, AD ∥ GF . As, segment AD is 11: EG = 1 1 + 1 AG ⇒ EG = 1 2 2 = 6 1 Thus, BE = BG − EG ⇒ BE = 1 − 6 1 ⇒ BE = 6 5
As, 5 & 6 are coprime, the answer is 5 + 6 = 1 1 .