Extrapolation

Calculus Level 5

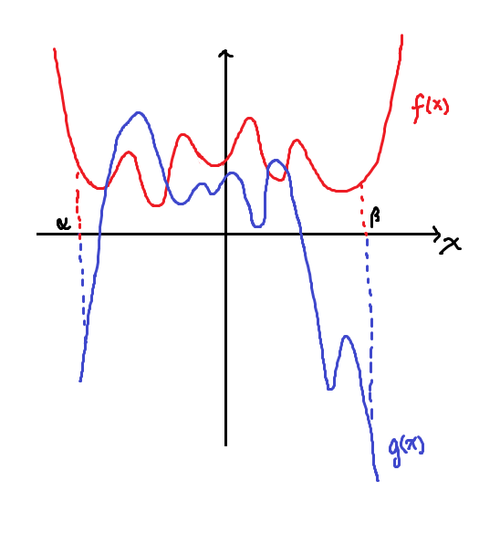Observe the graph above. The graphed functions $f(x), g(x)$ are both polynomials in $x$ with $f(x)$ being a degree 10 polynomial.

It is given that $f(x)$ is monotonically decreasing in the interval $(-\infty, \alpha)$ and monotonically increasing in the interval $(\beta, \infty)$ ; $g(x)$ is monotonically increasing in the interval $(-\infty, \alpha)$ and monotonically decreasing in the interval $(\beta, \infty)$ .

With this information, if $x_{f, m}, x_{g, n}$ are the (not necessarily distinct, possibly complex) roots of $f(x), g(x)$ respectively, find the maximum possible value of

$\deg(f) \cdot \deg(g) \cdot \text{sgn} \left (\prod_{m=1}^{\deg(f)} x_{f, m} \right ) \cdot \text{sgn} \left (\prod_{n=1}^{\deg(f)} x_{g, n} \right )$

where $\deg(f)$ is the degree of $f$ and $\text{sgn}(x)$ is the sign function .

The answer is -100.

1 solution

Jake Lai
Jan 31, 2015

Lemma 1:

The degree of a polynomial $f$ is equal to one more than the number of local extrema. (Include inflection points with tangent $0$ as "local extrema".)

If $\frac{d}{dx} f(x) = 0$ has $n-1$ solutions, it follows that $f(x)$ has $n-1$ local extrema and degree $n$ .

Lemma 2:

If an even-degree polynomial is "smiling", the product of its roots follows the sign of the $y$ -intercept. If an even-degree polynomial is "frowning", the product of its roots have the reverse sign of the $y$ -intercept.

By Vieta's formulas, $\prod x_{i} = \frac{a_{0}}{a_{n}}$ where $x_{i}$ are the roots of the even-degree polynomial. Since an even-degree polynomial is "smiling" when $a_{n} > 0$ and "frowning" when $a_{n} < 0$ , the sign of the product depends on $a_{0}$ , ie the $y$ -intercept.

Solution:

From Lemma 1, we know that $\deg(f) = \deg(g) = 10$ . From Lemma 2, we also know that the sign of the first product is $1$ and the sign of the second is $-1$ ! Hence, our expression becomes $\boxed{-100}$ .

I moved this into calculus.

I disagree with your conclusion that "from Lemma 1, we know that $\deg f = \deg g = 10$ . What we know is that $\deg f \geq 10$ , because some of these could be repeated roots.

Calvin Lin Staff - 6 years, 4 months ago

If there happen to be repeated roots, would there not (sometimes) be inflection points with derivative 0? I might be mistaken about this point.

Also, I've changed the answer to "maximum possible value of...".

Jake Lai - 6 years, 4 months ago

Your problem doesn't prohibit having inflection points with derivative 0.

For example, the graphs of $y = ( x-\alpha)^2 ( x - \beta)^2$ and $x-\alpha)^4 ( x - \beta)^4$ look the same graphically, and cannot be distinguished by your conditions.

Also, don't you want the maximum? Since the product is always negative.

Calvin Lin Staff - 6 years, 4 months ago

@Calvin Lin – Yup, changed it to maximum.

Jake Lai - 6 years, 4 months ago

I did everything the same except the part where you showed the product of roots. The product of signs functions of complex roots has to be 1 since they are complex conjugates of each other and for real roots can be checked from graph

Rohit Shah - 6 years, 3 months ago

Extrapolation

The answer is -100.

1 solution

0 pending reports