Extreme Ratios
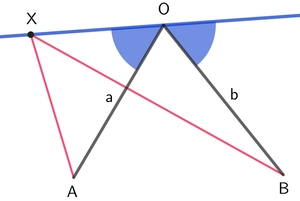 In the given figure,
X
is a variable point on a line which is equally inclined to the segments
A
O
and
B
O
.
In the given figure,
X
is a variable point on a line which is equally inclined to the segments
A
O
and
B
O
.
Let A O = a , B O = b and x = B X A X .
Find the product of the minimum and the maximum value of x .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Denote
∠
O
A
B
,
∠
O
B
A
, by
∠
A
and
∠
B
respectively.
Denote the length of
A
B
by
c
, the directed length of
O
X
by
t
and the measures of the noted angles by
θ
and
ϕ
(figure 1).
 figure 1
By cosine rule on triangles
△
O
A
X
,
△
O
B
X
we have
figure 1
By cosine rule on triangles
△
O
A
X
,
△
O
B
X
we have
A
X
2
=
t
2
−
2
a
t
cos
θ
+
a
2
,
B
X
2
=
t
2
−
2
b
t
cos
(
π
−
θ
)
+
b
2
⇒
B
X
2
=
t
2
+
2
b
t
cos
θ
+
b
2
.
It is sufficient to find the extrema of the function
f
(
t
)
:
=
B
X
2
A
X
2
=
t
2
+
2
b
t
cos
θ
+
b
2
t
2
−
2
a
t
cos
θ
+
a
2
.
The derivative of
f
is given by
f
′
(
t
)
=
(
t
2
+
2
b
t
cos
θ
+
b
2
)
2
2
(
a
+
b
)
[
cos
θ
⋅
t
2
−
(
a
−
b
)
⋅
t
−
a
b
cos
θ
]
The zeros of
f
′
are the roots of the quadratic
cos
θ
⋅
t
2
−
(
a
−
b
)
⋅
t
−
a
b
cos
θ
, who’s discriminant is
Δ
=
(
a
−
b
)
2
+
4
a
b
cos
2
θ
=
a
2
+
b
2
+
2
a
b
(
2
cos
2
θ
−
1
)
=
a
2
+
b
2
+
2
a
b
cos
(
2
θ
)
=
a
2
+
b
2
+
2
a
b
cos
(
π
−
φ
)
=
a
2
+
b
2
−
2
a
b
cos
φ
=
c
2
Hence,
f
is extremal when
t
=
2
cos
θ
a
−
b
+
c
=
cos
θ
s
−
b
:
=
t
1
o
r
t
=
2
cos
θ
a
−
b
−
c
=
−
cos
θ
s
−
a
:
=
t
2
(
1
)
where
s
=
2
a
+
b
+
c
is the semiperimeter of
△
O
A
B
.
 figure 2
figure 2
Now, consider the excircle
(
I
B
,
I
B
Y
1
)
of
△
O
A
B
tangent to the sides
B
O
,
B
A
at
Y
1
and
Y
2
respectively (figure 2).
Then,
B
Y
1
=
B
Y
2
=
2
1
(
a
+
b
+
c
)
=
s
Thus,
∣
∣
O
Y
1
∣
∣
=
s
−
b
=
t
1
cos
θ
Likewise, if the excircle
(
I
A
,
I
A
Z
1
)
on
O
B
is tangent to the sides
A
O
,
A
B
at
Z
1
and
Z
2
respectively, then
∣
∣
O
Z
1
∣
∣
=
s
−
a
=
−
t
2
cos
θ
Therefore, according to ( 1 ) , the extremal values of f occur when the point X coinsides with the excenters I B and I A , whose projections on the lines B O and A O are Y 1 and Z 1 respectively.
Now, by sine rule on triangles △ I A A B and △ I B A B , it is easy to see that I B B I B A = sin ( A + 2 π − A ) sin 2 B = cos 2 A sin 2 B a n d I A B I A A = sin 2 A sin ( π − 2 π − B ) = sin 2 A cos 2 B
Consequently, the required product of the minimum and the maximum value of the ratio x = X B X A is I B B I B A ⋅ I A B I A A = cos 2 A sin 2 B ⋅ sin 2 A cos 2 B = sin A sin B = b a .
Let p = O X , θ be one of the blue angles, and c = cos θ .
By the law of cosines on △ O X A , A X = p 2 + a 2 − 2 a p cos θ = p 2 + a 2 − 2 a p c , and by the law of cosines on △ O X B , B X = p 2 + b 2 − 2 b p cos ( 1 8 0 ° − θ ) = p 2 + b 2 + 2 b p c , so x = B X A X = p 2 + b 2 + 2 b p c p 2 + a 2 − 2 a p c .
For the maximum and minimum values of x , d p d x = ( p 2 − 2 a c p + a 2 ) ( p 2 + 2 b p + b 2 ) 3 ( a + b ) ( c p 2 − ( a − b ) p − a b c ) = 0 , which solves to p = 2 c a − b ± ( a − b ) 2 + 4 a b c 2 .
Substituting these p values back into x gives maximum and minimum values of x = 2 b 2 ( 1 − c 2 ) a 2 + 2 a b c 2 + b 2 ± ( a + b ) ( a − b ) 2 + 4 a b c 2 .
The product P of the maximum and minimum values of x is therefore:
P = 2 b 2 ( 1 − c 2 ) a 2 + 2 a b c 2 + b 2 + ( a + b ) ( a − b ) 2 + 4 a b c 2 ⋅ 2 b 2 ( 1 − c 2 ) a 2 + 2 a b c 2 + b 2 − ( a + b ) ( a − b ) 2 + 4 a b c 2 = 2 b 2 ( 1 − c 2 ) ( a 2 + 2 a b c 2 + b 2 ) 2 − ( a + b ) 2 ( ( a − b ) 2 + 4 a b c 2 ) = 2 b 2 ( 1 − c 2 ) 2 a b ( 1 − c 2 ) = b a .
This question is very much related to triangle geometry. The extreme points are notable points for triangle O A B . Can you figure out what they are?
Log in to reply
I solved the same way as @David Vreken . Now I see that these extreme points are the excenters of △ O A B that correspond to the sides O A and O B . Although, I'm still trying to figure out the reason for this coincidence. Give us some time :)
Log in to reply
try this problem
I hadn't noticed that they were excenters. Nice observation!
Log in to reply
@David Vreken – @Digvijay Singh Thank you, it was very helpful!
Log in to reply
@Thanos Petropoulos – @David Vreken @Digvijay Singh @Thanos Petropoulos You might like to look at the (new) second half of my proof, which gives an entirely geometric proof of this result.
Log in to reply
@Mark Hennings – Excellent geometric approach!
If we reflect point B in the line L , we obtain B ′ where A , O and B ′ are collinear, and the ratios X B A X and X B ′ A X are equal. The locus of the set of points X for which X B ′ A X is a given constant k is a circle in which A and B ′ are mutually inverse points (except when k = 1 , in which case the locus is the perpendicular bisector of A B ′ ). Thus, to extremize x = X B A X = X B ′ A X , we need to find the two such circles which are tangent to the given line L . Let θ be the common angle of incidence of A O and B O to the line L .
The first of these circles has centre C 1 on the extended line A B ′ , and has radius R where ( R csc θ − a ) ( R csc θ + b ) R 2 cot 2 θ − ( a − b ) R csc θ − a b = R 2 = 0 while the second circle has centre C 2 on the extended line A B ′ and radius S where ( S csc θ + a ) ( S csc θ − b ) S 2 cot 2 θ + ( a − b ) R csc θ − a b = S 2 = 0 and hence R = sec θ [ X + 2 1 ( a − b ) tan θ ] S = sec θ [ X − 2 1 ( a − b ) tan θ ] where X = 2 1 ( a − b ) 2 tan 2 θ + 4 a b sin 2 θ so that R S = a b tan 2 θ R − S = ( a − b ) tan θ sec θ The extreme values of x are obtained when the point X is at either X 1 or X 2 , the points of tangency of these circles with the line L , and hence x 1 = R R csc θ − a x 2 = S csc θ − b S = S S csc θ + a so that x 1 x 2 = R S ( R csc θ − a ) ( S csc θ + a ) = R S R S csc 2 θ + a ( R − S ) csc θ − a 2 = b a
Now let's work the problem the other way. Suppose that X 1 , X 2 are the excentres of the triangle O A B opposite B and A respectively. Then X 1 , O and X 2 are collinear, all lying on the line L . Let C 1 and C 2 be the intersections with the line A O B ′ with the lines perpendicular to L passing through X 1 and X 2 respectively.
Now X 2 is on the angle bisector of ∠ O A B , so ∠ O A X 2 = ∠ B A X 2 = α . Moreover X 1 is on the angle bisector of ∠ O B A , so ∠ O B X 1 = ∠ A B X 1 = β . Moreover ∠ O A X 1 = 9 0 ∘ − α and ∠ O B X 2 = 9 0 ∘ − β , so we deduce that ∠ X 1 A X 2 = ∠ X 1 B X 2 = 9 0 ∘ . Thus we deduce that X 1 , X 2 , A , B are concyclic, with the centre of the circumcircle lying on the line L , which means that B ′ also lies on this circle. Thus we deduce that ∠ B X 1 X 2 = ∠ X 2 X 1 B ′ = α and X 1 B ′ A = X 1 X 2 A = β , while ∠ B ′ O X 2 = α + β .
Since ∠ A X 1 B = 9 0 ∘ − α − β , we deduce that ∠ C 1 X 1 A = β . This means that triangles C 1 A X 1 and C 1 X 1 B ′ are similar, which implies that C 1 A × C 1 B ′ = C 1 X 1 2 , and hence that A , B ′ are mutually inverse in the circle with centre C 1 that passes through X 1 (which is therefore tangent to L .
Since ∠ O B ′ X 2 = 9 0 ∘ − β , we see that ∠ O X 2 B ′ = 9 0 ∘ − α , so that ∠ B ′ X 2 C 2 = α . This means that the triangles C 2 B ′ X 2 and C 2 X 2 A are similar, which implies that C 2 A × C 2 B ′ = C 2 X 2 2 , and hence that A , B ′ are mutually inverse in the circle with centre C 2 that passes through X 2 (which is therefore tangent to L ). Thus the points X 1 , X 2 , C 1 , C 2 are the same as the ones previously defined. The Sine Rule now gives sin β A X 1 = sin ( 9 0 ∘ + α ) B X 1 = cos α B X 1 cos β A X 2 = sin ( 9 0 ∘ + β ) A X 2 = sin α B X 2 and hence x 1 = B X 1 A X 1 = cos α sin β x 2 = B X 2 A X 2 = sin α cos β so that x 1 x 2 = sin α cos α sin β cos β = sin 2 α sin 2 β = O B O A = b a