Extreme Yin-Yang

image

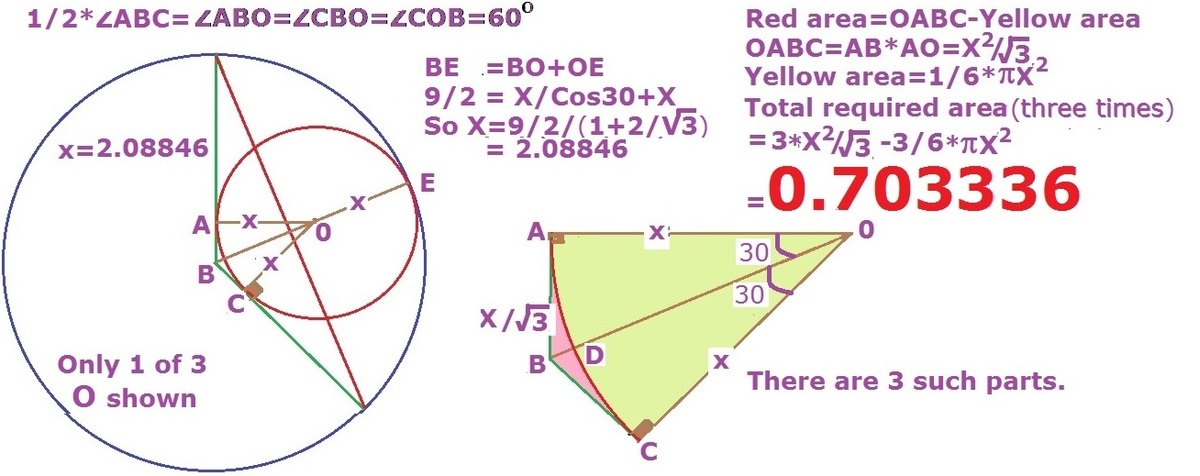
This basically summarizes what it will look like and provides a visual representation of how to solve the problem.

We start by finding the radius of the smaller circles which will be (x=radius of the smaller circles because they are the same size) $9=x+\dfrac{2x\sqrt3}{3}\longrightarrow x=18\sqrt3-27$ . Then, because the circles are of the same size and the angles of the triangle add up to 180, the sectors of the circle contained in the triangle will add up to 1/2 the area of the circle. After some messy calculations, which I'm too lazy to type out (basically squaring the value of x above and multiplying that by $sqrt(3)-\pi$ ), we find the area of the triangular sector in the middle to be $\boxed{2.813}$ .

This may be wrong because I tested multiple other possible scenarios and found a $\textit{general}$ proof for 2 circles being smaller and of the same radii, but not for all three being different. Using logic, however, it seems that it won't yield the max value using that method.