Extremes with Equilaterals

Two concentric circles with center O have radii of 2 0 and 1 4 .
Two points A and B are drawn such that A is on the circle of radius 2 0 , and B is on the circle with radius 1 4 .
A point P is drawn so that △ A P B is equilateral.
If the maximum possible distance of O P is M , and the minimum is m , then find M × m .
The answer is 204.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Pompeiu's Theorem kills this problem. Expect to see some less trivial problems using Pompeiu's from me; I'm currently studying it from a book I got at a competition.
Log in to reply
Aw nartz I didn't know that theorem. What competition?
Log in to reply
I think I have seen it in Amc problem but i donot remember
Log in to reply
@Mardokay Mosazghi – How'd you do on AMC's?
Log in to reply
@Finn Hulse – Never took the 10 grade one but on AMC 8 I got 20/25 marks. @Finn Hulse
Log in to reply
@Mardokay Mosazghi – Nice dude. The AMC 8 for 2014 was before I ever started math. I got a 16, which kind of inspired me to get better at math. Slacked off, and did terribly on AMC 10 too. Next year though... :O
Log in to reply
@Daniel Liu – Oh nice. Did you win?
Log in to reply
@Finn Hulse – No, I got 2nd place along with 4 other people; 3 people got 1st from solving all 7 problems. I only solved 6.
Log in to reply
@Daniel Liu – Dude it's okay I already saw the page. Dude I'm cool like that. :D
Also it is perfectly possible to solve the problem without the theorem, but the theorem makes it a lot more convenient.
what if O, A, B are collinear then m and M are same but their product doesnt equals 204 .. !!
Log in to reply
Well, if A, O, and B are collinear, it doesn't give the maximum nor the minimum. I'm not exactly sure what's confusing you.
Log in to reply
if A, O, and B are collinear then the maximum and minimum values are the same .. !! since the only condition given is the points A and B should be on the circle ... and the maximum and minimum value are independent of any desired position ... then the collinear case can be considered where its easy to find the length OP... ! but this approach doesn't agrees with your up voted solution .. !
This reminds me of an old AIME problem on the 2012 test.
I think it would be more challenging if this problem asks to sketch the corresponding point P to the extrema. I hypothesize that it may be sketch-able via straightedge and compass. Two more questions for those who love to take a deeper look. Interesting problem anyway!
 Figure
Figure
If O B is fixed and A moves along the red circle, then P also moves along a congruent circle (purple). This purple circle is obtained by rotating the red one by 6 0 ° with center in B ... well in fact is − 6 0 °
This means that the center Q of this second circle forms an equilateral triangle O B Q .
Given that O Q = 1 4 and the radius of this purple circle is 2 0 , is easy to find that m = 6 and M = 3 4 ... and the answers is 2 0 4 .
:)
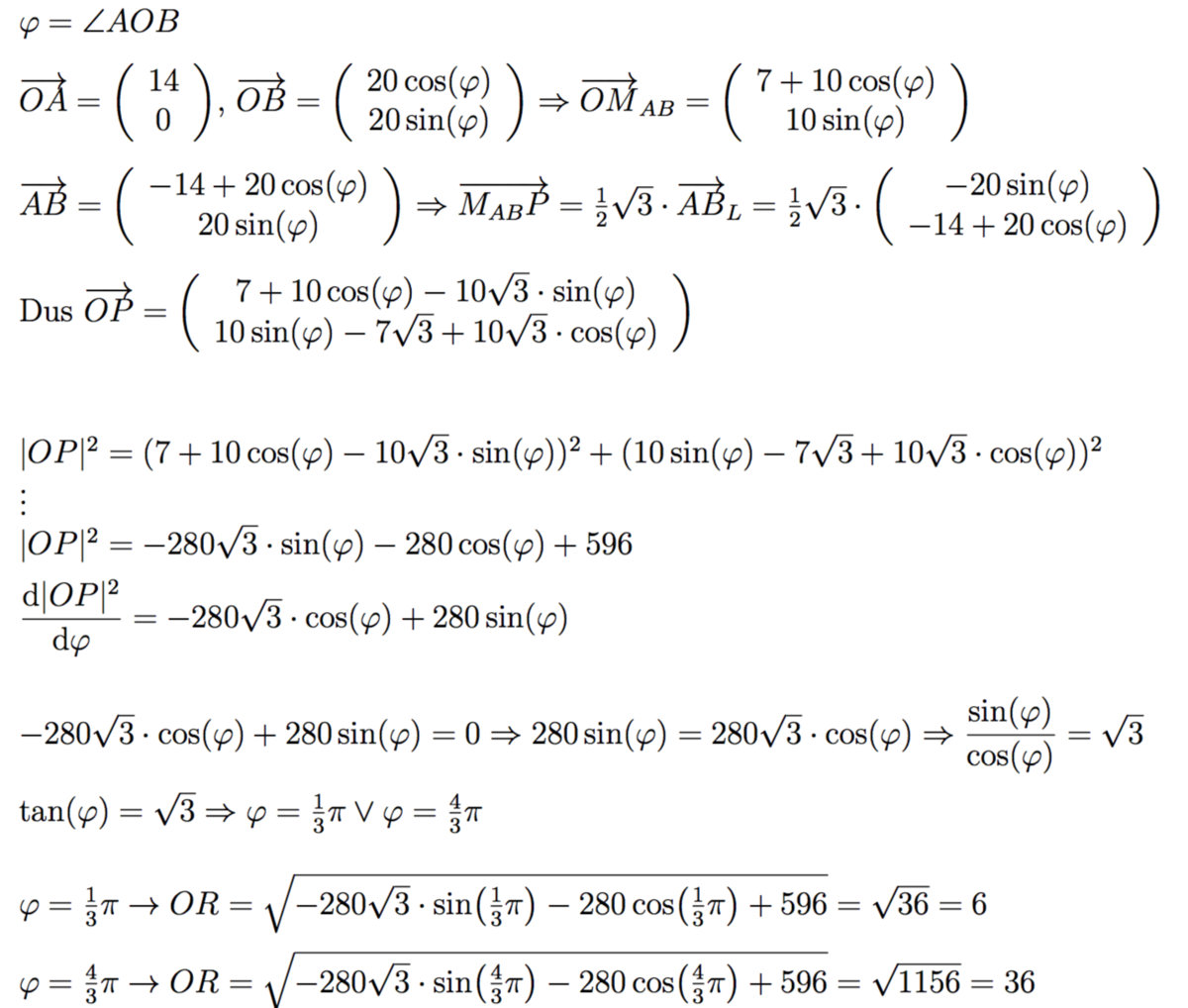
Draw the circle with radius O P . By Pompeiu's Theorem, the line segments O P , O A , and O B can make a (possibly degenerate) triangle. Thus, by the triangle inequality, O A + O B ≥ O P and O B + O P ≥ O A . We know that O A = 2 0 and O B = 1 4 . Thus, 2 0 + 1 4 ≥ O P ⟹ O P ≤ 3 4 1 4 + O P ≥ 2 0 ⟹ O P ≥ 6
Thus, M = 3 4 and m = 6 so our answer is 6 × 3 4 = 2 0 4 .