Two Famous Formulae
1 3 + 2 3 + ⋯ + n 3 = 1 + 2 + ⋯ + n
For all positive integers n , is the above equation true or false?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
YES .IT'S IS MY ANSWER.
Did the same Thing
This can actually be illustrated with the use of a simple multiplication table, that children use to learn how to multiply. Here is a multiplication table
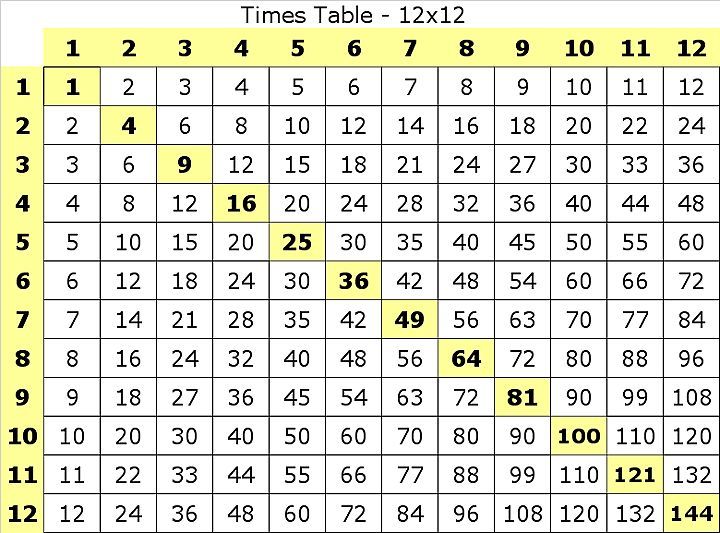
Notice that given any n × n array of numbers with 1 at the upper left corner, the sum of all the numbers in the array equals the square of the sum of all the numbers in the top row. For example, for n = 4 , we have
1 + 2 + 3 + 4 = 1 0
1
+
2
+
3
+
4
+
2
+
4
+
6
+
8
+
3
+
6
+
9
+
1
2
+
4
+
8
+
1
2
+
1
6
=
1
0
0
which is the sum of the first n cubes
1 + 8 + 2 7 + 6 4 = 1 0 0
The cubes can be found by adding the numbers "around the corner", i.e.
1
=
1
2
+
4
+
2
=
8
3
+
6
+
9
+
6
+
3
=
2
7
4
+
8
+
1
2
+
1
6
+
1
2
+
8
+
4
=
6
4
so that everything is accounted for.
That's a good answer. I have found this equation when I was 13 years old .And I haven't the answer until I am 16 years old . You are excellent.
Log in to reply
Well, this isn't actually a "proof". Rather, it's an interesting observation that can be made about the multiplication table. Actually proving this takes a few more steps.
Log in to reply
can you show ?
Log in to reply
@Nguyễn Hưng – Sure. For this example where n = 4
First note that
1
+
2
+
3
+
4
+
2
+
4
+
6
+
8
+
3
+
6
+
9
+
1
2
+
4
+
8
+
1
2
+
1
6
=
1
(
1
+
2
+
3
+
4
)
+
2
(
1
+
2
+
3
+
4
)
+
3
(
1
+
2
+
3
+
4
)
+
4
(
1
+
2
+
3
+
4
)
=
( 1 + 2 + 3 + 4 ) 2
Then note that
4
+
8
+
1
2
+
1
6
+
1
2
+
8
+
4
=
(
4
+
1
2
)
+
(
8
+
8
)
+
(
1
2
+
4
)
+
(
1
6
)
=
1
6
+
1
6
+
1
6
+
1
6
=
4
(
1
6
)
=
4
3
which is the same pattern for other cubes, so that we end up with
( 1 + 2 + 3 + 4 ) 2 = 1 3 + 2 3 + 3 3 + 4 3
In vietnam ,the children don't study by multiplication table similar to your country .
I read the question wrong... The answer can also be demonstrated using the formula for sums.
yes .You are true
1 3 + 2 3 + ⋯ + n 3 = 4 n 2 ( n + 1 ) 2 = 2 n ( n + 1 ) = 1 + 2 + ⋯ + n