Fancy Parties
A and E each have 3 friends, whereas B, C, and D each have 2 friends.
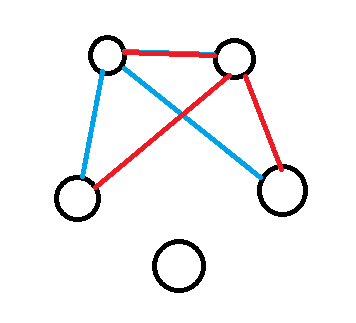
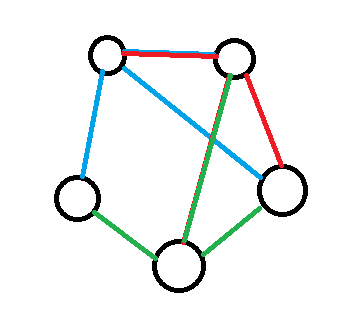
In a party with 5 people, it is possible that 2 people have 3 friends and 3 people have 2 friends, as shown in the graph to the right.
In a party with 5 people, is it possible that there are 3 people with 3 friends and 2 people with 2 friends?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
20 solutions
I do not understand your explanation starting where it says ' ...sum of all the "friends"... has to be even' and afterwards.
Log in to reply
If there is a friendship, there are two people who are being friends. So if there are, say, three friendships, that means if you count for each person all of his/her friends, you end up with an even number.
Log in to reply
Then how did you come up with formula 3 x 2 + 2 x 2 ?
Log in to reply
@A Former Brilliant Member – 3 people with 3 friends and 2 people with 2 friends
3 people with 3 friends -> 3 * 3
2 people with 2 friends -> 2 * 2
All together -> 3 * 3 + 2 * 2
This is why the language of mathematics was invented. What's meant here is "the sum of the degrees of a graph has to be even because it equals twice the number of edges of a graph."
3 x 2 + 2 x 2 = 10 bruh
Log in to reply
The problem wants the three people to have 3 friends each (3x3) not 2 each (3x2).
Couldn’t a pair of people be friends with each other whilst a group of three are friends also all friends ? 3x2+2x2
Log in to reply
The first mistake in your thinking is the confusion coming from the statement a pair of people being friends with eachother.
You are asked for a scenario with 3 people having 3 friends and 2 having 2 (total 5 people).
When you say a pair of people being friends you are either redding to one friendship (A to B) or a group of four each having four each having two friends (A to C and D only, and B to C and D only)
Neither satisfies the question
In your scenario, there is indeed a group of 3 friends and a group of 2 friends. However, in the group of 3, each person only has 2 friends each, and the group of 2 is just a simple friendship where each person has one friend. If you think about this backward, this is similar to how if you have two siblings, your parents have 3 kids overall, and if you have one sibling your parents have 2 kids overall (including you).
it doesn't matter
I love this app
3×3 is 9 + 2 is 11 × 22 is 22 22 is an even number yes is the answer
I agree with you
Although I can't even understand this problem
When one does not understand this statement, one should study graph theory.
This could also viewed by the pigeonhole principle wherease 13 holes(sum of all friend everyone has) cannot be filled by the friendships themselves(as each friendship contains two friends).
If a person has n friends, then there must be n edges attached to that person in the corresponding friendship graph (in other words, the degree of the node is n). The total degree of the graph is the sum of the degrees of the individual nodes.
Adding an edge to the graph contributes +2 to the total degree (+1 to the degrees of the two nodes that the edge connects). Therefore the total degree must be even, since it is equal to 2 times the number of edges.
The situation described corresponds to 3 nodes of degree 3, and 2 nodes of degree 2, which gives: 3 × 3 + 2 × 2 = 1 3 = 2 × number of edges which is odd, and therefore impossible.
i tried and its no for answer;.
We can visualize the problem by creating a case (you may choose anyone and the eventual outcome will be the same) for the following 5 persons:
A B C D E
-
Let A have 3 friends: B C D
-
Let B have 3 friends: A C D (A was already connected to B in 1.)
-
Let C have 3 friends: A B E (C was already connected to A and B in 1. and 2.)
We have fulfilled the 3 persons 3 friends criteria.
-
This means D definitely has 2 friends: A and B as per the above conditions.
-
Similarly, E has C as a friend. Now E cannot add either A, B or D as a friend because it will violate the 3 persons 3 friends condition in order to generate 2 persons 2 friends condition.
Thus, it is impossible to achieve such an overall condition.
Hi. Why can't the two people be friends with each other, and the three with each other. Did I miss that they all need to be connected?
Log in to reply
If the three people are friends with each other, they only have two friends. A with B,C ... B with A,C ... C with A,B ... They need to have another person involved.
I just did it. 3 friends with 3 friends each and 2 friends with 2 friends each. There is no mention that a person cannot have a friend that is already a friend of someone else.
Log in to reply
Draw a tree network diagram to understand my point. Just draw it and you will see how the violation occurs.
C and D can have 3 friends A E and B can have 2 friends by joining C B and D in the picture.
Log in to reply
Then B will have 4 friends, including A and E. So the criteria asked gets violated.
give an example,and try to prove it's right or not,this method is good
In the language of Graph Theory,
Sum of degrees of the vertices of an undirected graph is always even.
Now, consider the people in the party as the vertices of a graph with number of friends of a person as the degree of the vertex representing the person.
Then 3 people with 3 friends and 2 people with 2 friends leave us with 3 × 3 + 2 × 2 = 1 3 (which is an odd number) as total degrees of vertices.
So, NO is the answer.
Start with Five People
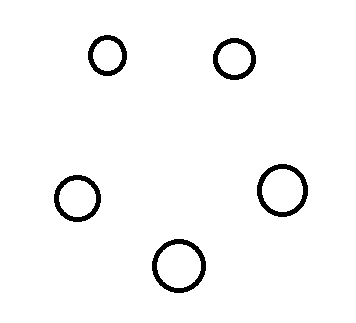 Pick any person to have three friends.
Pick any person to have three friends.
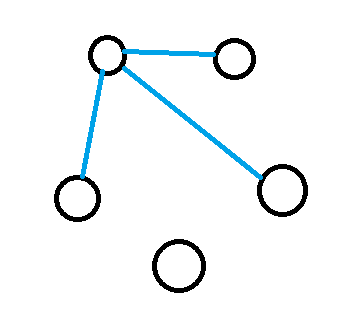 Now we have choices. We can make our second three friend guy a friend or not.
Let's make him not a friend.
Now we have choices. We can make our second three friend guy a friend or not.
Let's make him not a friend.
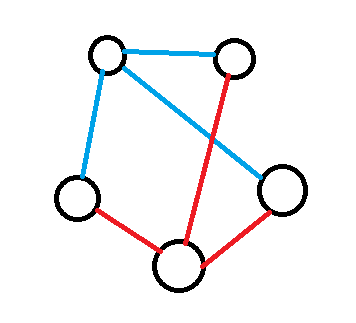 Now we have three friends who have two friends, and two with three. Unfortunately, whoever we choose to upgrade to three friends will then have another friend with three friends, so it won't work.
Now we have three friends who have two friends, and two with three. Unfortunately, whoever we choose to upgrade to three friends will then have another friend with three friends, so it won't work.
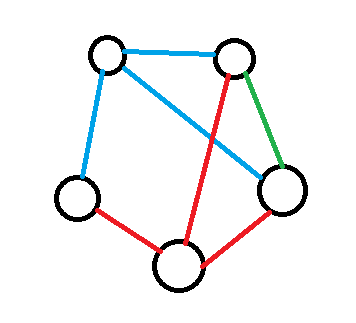
So we try making him a friend of our first guy, He can only be friends with first guy's friends, or with the other one. Let's have him with first guy's friends only
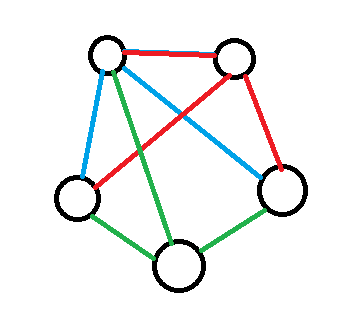
Then, our third friend with three firends is a friend of the first firend, or not. If he's not, then we get too many friends.
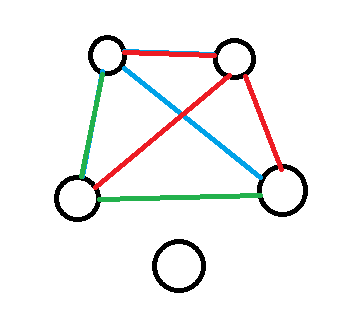
 If he is, then we have a lonely friend :(
If he is, then we have a lonely friend :(
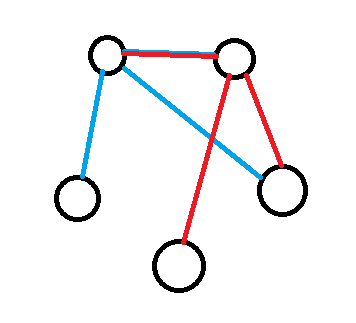
If our second friend is friends with the last friend, then we are again forced to pick the third three-friend to have too many friends.
Sum of all the "friends" has to be even. 3 3 + 2 2 = 13 (odd) So it is not Possible, so such situation is impossible.
33 + 22 = 55 not 13.
according to the graph,
A & E is directly connected with B,C,D—–3 people
B,C, & D is directly connected with A,E——–2 people
it is clearly seen that,2 people with 3 friends is possible but 3 people with 3 friends is not possible in 2 dimension
not possible, simply because there are just 5 people!
we have only five people so for 3friends and 3 people it will be 6people
okokokigetit.
There are a theorem in graphs theory, and says; in a graph, there is an even number of vertex of odd degree. So, in the problem there are 3 people with 3 friends, in a graph, thus is, an odd number of vertex of odd degree.
Assuming that 3 unique persons are going to befriend 3 similar others, this means there should be at least 6 persons, hence it is impossible.
I DO NOT WANT TO COMMENT ON THIS SOLUTION (the odd number of 3x3 + 2x2 which I hadn't noticed is a very good solution!). I WISH TO ASK A QUESTION! Which is how do you make a comment about a question before you have answered it. In particular what does the notation of a line over 3 variables abc mean which is the notation used in the question of this week. (I suppose that I'll just come back here to see if anyone has been kind enough to answer my question?) The general question that I've asked is a valid one I think. Is there a 'platform' to ask questions such as 'what does this notation mean'? Regards, David
There are 5 persons in the group (including yourself). The maximum number of friends you could have is 4 (you have to exclude "yourself"). Thus n-1. 5 -1 = 4. Given the supplied network diagram, it would be impossible.
Seeing all these mathematical formulas...it's way simpler:
If three people have three friends the total would be 6 people. Can't be cause there are 5 people total...
That is not true. Imagine a group of four people, all being friends to each other. Then you have four people who have three friends each, yet only four people in total. So no, you don't need 6 people to have three people with three friends; the thing is, they can be friendships between the three "initial" people, so one doesn't need three more people necessarily (though at least one more person is needed, because one can't be friends with themselves, so in a group of three, one can have at most two friends)
The problem can be modelled as an undirected graph. In essence one uses the Handshake-Theorem, which says that the sum of all the numbers of neighbors any vertex has (called degree of the vertex) must be two times the number of total edges in the graph. This implies that an undirected graph may not have an odd number of vertices with an odd number of neighbors, which would be the case in our model, if 3 people at a party had 3 friends.
This is a basic example of euler's characteristic for connected planar graphs (V-E+F = 2) ? Correct?
The number of vertices of odd degree is always even in an undirected graph. There are three nodes with odd degrees (Three people with three friends). Therefore, no such graph exists.
Seen as their are only 5 people, and 3 of these have 3 friends. So that leaves us with only 2 people left, and they can't be friends with any of the other 3 seen as they only have 3 friends.
In every graph, the sum of degrees of each vertex must be double of the total number of edges. Since (3 3)+(2 2) = 9+4 = 13, and 13 is odd, we can conclude that such a graph is not possible.
For every friendship there have to be two people, one on each end of the relationship, who are being friends.
So the sum of all the "friends" of all the people has to be even.
3 × 3 + 2 × 2 = 1 3
Since 13 is odd, it may not be an answer, so such situation is impossible.