Fancy Points on Ellipse
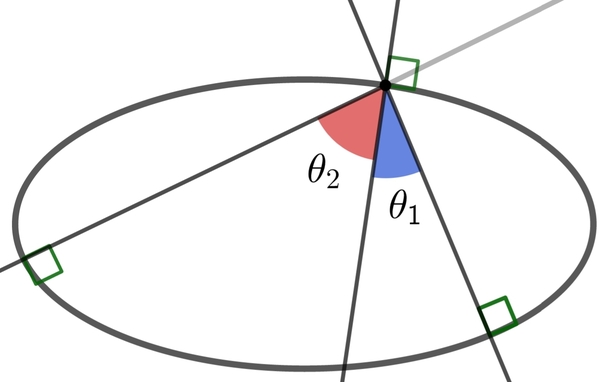
A point on an ellipse is such that, exactly three distinct normals to the ellipse pass through this point (as shown).
Define θ 1 and θ 2 as shown in the figure, where θ 2 > θ 1 .
Find tan θ 2 tan θ 1 .
The answer is 0.5.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
In general, let P be the point in the plane of ellipse through which exactly three normals can pass.
Then P is always of the form ( a a 2 − b 2 cos 3 θ , b a 2 − b 2 sin 3 θ )
And the slopes of the normals are:
-
m 1 = − b a tan θ
-
m 2 , m 3 = b a tan θ ( sec 2 θ ± tan 4 θ + sec 2 θ )
Log in to reply
Was your solution also same as the above solution? and can you provide a proof of your claim or a link... because these calculations are really tedious and lengthy....
Log in to reply
And if you want to find the slopes of the normals you would have to deal with a quartic equation (you can see this in my previous problems on ellipses).
Fortunately, the solutions to the quartic equation are simple in this case.
Also, I solved this problem in a very similar way as David Vreken.
Let the ellipse have an equation of a 2 x 2 + b 2 y 2 = 1 , where a > b . Then by rearranging the equation, any point on the ellipse can be expressed as ( k , ± a b a 2 − k 2 ) .
Using implicit differentiation on the equation of the ellipse, a 2 2 x + b 2 2 y y ′ = 0 , which solves to y ′ = − a 2 y b 2 x , so the slope of a normal line perpendicular to the slope of the tangent line is b 2 x a 2 y , and if it through an x -coordinate of k its slope is ± b k a a 2 − k 2 and its equation is y = ± b k a a 2 − k 2 ( x − k ) ± a b a 2 − k 2 or y = ± a b k a 2 − k 2 ( a 2 x + ( a 2 − b 2 ) k ) .
Without loss of generality (and to match the given picture), let the point with three distinct normals be point P in the first quadrant with coordinates ( k 1 , a b a 2 − k 1 2 ) , let another point of normalcy be Q in the fourth quadrant with coordinates ( k 2 , − a b a 2 − k 2 2 ) , and let the third point of normalcy be R in the third quadrant with coordinates ( k 3 , − a b a 2 − k 3 2 ) . Also let S be a point on the normal through P not through R or Q .
Using the equations above, the slope through P S is m 1 = b k 1 a a 2 − k 1 2 , the slope through P Q is m 2 = − b k 2 a a 2 − k 2 2 , and the slope through P R is m 3 = − b k 3 a a 2 − k 3 2 , and the equations for P Q and P R are y = − a b k a 2 − k 2 ( a 2 x + ( a 2 − b 2 ) k ) for k = k 2 and k = k 3 , respectively.
Since P ( k 1 , a b a 2 − k 1 2 ) is on both P Q and P R , we have:
a b a 2 − k 1 2 = − a b k a 2 − k 2 ( a 2 k 1 + ( a 2 − b 2 ) k )
which after rearranging simplifies to:
k 4 − a 2 − b 2 2 a 2 k 1 k 3 + ( a 2 − b 2 ) 2 ( a 4 − b 4 ) k 1 2 − a 4 ( a 2 − 2 b 2 ) k 2 + a 2 − b 2 2 a 4 k 1 k − ( a 2 − b 2 ) 2 a 6 k 1 2 = 0
where the roots of this equation represent the x -coordinates of all the points of normalcy that go through P . Being a quartic equation suggests that up to 4 distinct normals can exist, but since we must have exactly 3 distinct normals this suggests there is a double-root. Also, one of these points includes P 's x -coordinate of k 1 , so fortunately we can factor ( k − k 1 ) to obtain:
( k − k 1 ) ( k 3 − a 2 − b 2 k 1 ( a 2 + b 2 ) k 2 − ( a 2 − b 2 ) 2 a 4 ( a 2 − 2 b 2 ) k + ( a 2 − b 2 ) 2 k 1 a 6 ) = 0
Without loss of generality, let the double-root be k 2 . Then ( k − k 1 ) ( k − k 2 ) 2 ( k − k 3 ) = 0 , or ( k − k 1 ) ( k 3 − ( 2 k 2 + k 3 ) k 2 + ( k 2 2 + k 3 ) k − k 2 2 k 3 ) = 0 , and comparing coefficients with this equation to the quartic equation above gives a system of equations where:
2 k 2 + k 3 = a 2 − b 2 k 1 ( a 2 + b 2 ) , k 2 2 + k 3 = − ( a 2 − b 2 ) 2 a 4 ( a 2 − 2 b 2 ) , k 2 2 k 3 = − ( a 2 − b 2 ) 2 k 1 a 6
which solves to:
k 1 = ( a 2 − b 2 ) ( a 2 + b 2 ) 3 a 4 ( a 2 − 2 b 2 ) 3 , k 2 = ( a 2 − b 2 ) ( a 2 + b 2 ) a 4 ( a 2 − 2 b 2 ) , k 3 = − ( a 2 − b 2 ) 3 ( a 2 + b 2 ) a 8 ( a 2 − 2 b 2 )
for k 1 > 0 , k 2 > 0 , and k 3 < 0 . Plugging these values into m 1 = b k 1 a a 2 − k 1 2 , m 2 = b k 2 a a 2 − k 2 2 , and m 3 = b k 3 a a 2 − k 3 2 as defined from above gives:
m 1 = ( a 2 − 2 b 2 ) 3 ( 2 a 2 − b 2 ) 3 , m 2 = − a 2 − 2 b 2 2 a 2 − b 2 , m 3 = a 4 ( a 2 − 2 b 2 ) b 4 ( 2 a 2 − b 2 )
Using the angle between two lines equation gives tan θ 1 = 1 + m 1 m 2 m 2 − m 1 = a 2 + b 2 ( a 2 − 2 b 2 ) ( 2 a 2 − b 2 ) and tan θ 2 = 1 + m 1 m 3 m 1 − m 3 = a 2 + b 2 2 ( a 2 − 2 b 2 ) ( 2 a 2 − b 2 ) = 2 tan θ 1 .
Therefore, tan θ 2 tan θ 1 = 2 tan θ 1 tan θ 1 = 2 1 = 0 . 5 .