Fancy Rectangle
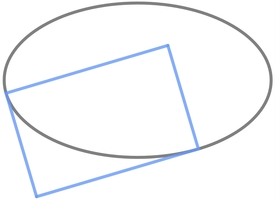
Let a and b be the lengths of the semimajor and semiminor axes of an ellipse respectively.
Draw a rectangle whose two sides are tangent to the ellipse and the other two are normal to the ellipse.
Find the area enclosed by the locus of the vertex of the rectangle at which the normals meet.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
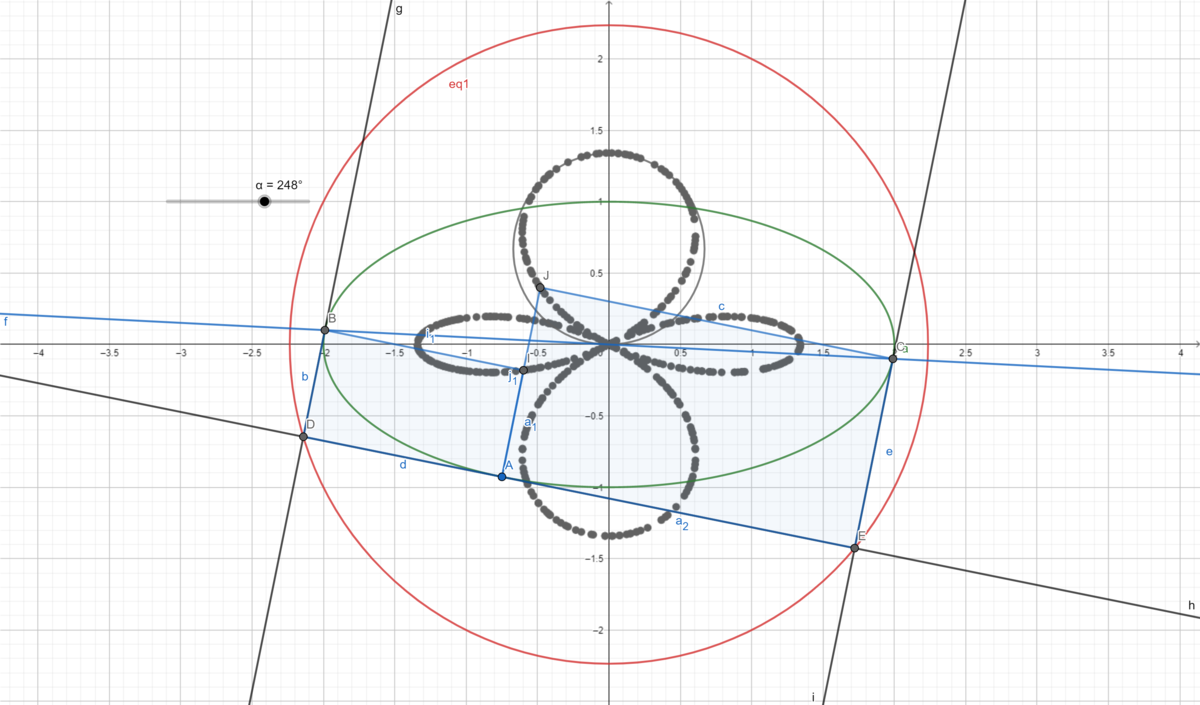 I felt it would be nice to add a picture, so here's a curve traced by the vertex where two normals meet (which looks like Lemniscate of Bernoulli). Also, it's interesting that the locus of points where tangents meet is a circle with radius
a
2
+
b
2
.
I felt it would be nice to add a picture, so here's a curve traced by the vertex where two normals meet (which looks like Lemniscate of Bernoulli). Also, it's interesting that the locus of points where tangents meet is a circle with radius
a
2
+
b
2
.
Log in to reply
I'm in 9th grade taking ap calculus bc I know I'm smart
@Digvijay Singh, How did you compute the equation in m by eliminating θ ? In the equation having a,h,b,m,k,e what is e ? Is it eccentricity of ellipse?
Log in to reply
Well, you have two equations in two variables m and θ . Eliminating θ is basic algebra and trigonometry. In the first equation, you can write sec θ = 1 + tan 2 θ and csc θ = tan θ 1 + tan 2 θ , now, from the other equation we have tan θ = a b m . Substitute this value in the first equation and simplify. And yes, e in the equation you're referring to, is the eccentricity of the ellipse.
Log in to reply
@Digvijay Singh – How did you eliminate m 1 , m 2 , m 3 , m 4 from the five equations of sums and products of roots of quartic equation in m?
Log in to reply
@Winod Dhamnekar – Well, it was tedious, it took me two pages, and i don't even remember it now.
Just do some clever algebra, you'll figure it out. ;)
Log in to reply
@Digvijay Singh – It is observed that while computing the quartic equation in 'm', you excluded this term 2 a 2 e 2 m a 2 + b 2 m 2 ∗ ( k − m h ) . why? Is it because if we put this term =0, then ( k − m h ) = 0 ⇒ k = m h which is impractical?
Log in to reply
@Winod Dhamnekar – I did not exclude any terms.
I eliminated the square root terms by squaring the equation.
Log in to reply
@Digvijay Singh – How to plot the locus of the vertex of the rectangle at which the normals meets in www.wolframalpha.com or on any other graphing appliction or calculator or in Octave?
How to plot the locus of the vertex of rectangle at which the normals meets in www.wolframalpha.com or in any other graphing application(calculator) such as in 'r' or in 'octave'?
WOW. Thats amazing
Alright, how area is equal to the given phrase
Digvijay Singh can you explain it to me in a simple english please
We are required to find the locus of the point ( h , k ) from which two mutually perpendicular lines can be drawn that are normal to the ellipse.
Normal to the ellipse at the point ( a cos θ , b sin θ ) is given by a x sec θ − b y csc θ = a 2 − b 2 and the slope of this normal is given by m = b a tan θ
Putting x = h , y = k and eliminating θ , we get a quartic equation in m
b 2 h 2 m 4 − 2 b 2 h k m 3 + ( a 2 h 2 + b 2 k 2 − a 4 e 4 ) m 2 − 2 a 2 h k m + a 2 k 2 = 0
This tells us that at most four normals can be drawn from the point ( h , k ) to the ellipse whose slopes are the solutions of the above equation.
Let m 1 , m 2 , m 3 , m 4 be the four solutions, and for our locus, let m 1 and m 2 be the slopes of the mutually perpendicular normals.
From theory of equations we get:
m 1 + m 2 + m 3 + m 4 = h 2 k
m 1 m 2 + m 1 m 3 + m 1 m 4 + m 2 m 3 + m 2 m 4 + m 3 m 4 = b 2 h 2 a 2 h 2 + b 2 k 2 − a 4 e 4
m 1 m 2 m 3 + m 1 m 2 m 4 + m 1 m 3 m 4 + m 2 m 3 m 4 = b 2 h 2 a 2 k
m 1 m 2 m 3 m 4 = b 2 h 2 a 2 k 2
and m 1 m 2 = − 1
Eliminating m 1 , m 2 , m 3 , m 4 from the above five equations (a very tedious yet fun exercise) , we get
( a 2 + b 2 ) ( h 2 + k 2 ) ( a 2 k 2 + b 2 h 2 ) 2 = ( a 2 − b 2 ) 2 ( a 2 k 2 − b 2 h 2 ) 2
This is the required locus. Converting this to polar form, h = r cos θ , k = r sin θ , we get
r = a 2 + b 2 a 2 − b 2 ( a 2 sin 2 θ + b 2 cos 2 θ a 2 sin 2 θ − b 2 cos 2 θ )
Now, the required area is 2 1 ∫ 0 2 π r 2 d θ
Which turns out to be ( a − b ) 2 π