Fastest King+Rook Mate
Find the minimum number of moves for White to checkmate Black.
White starts, and Black plays optimally.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
The board is backwards ....
Log in to reply
Pretend your a spectator from the side:)... without paws on the board it doesnt matter
I can simply put white king in front of black one...
It's 2 moves!!! Black king can I to h1!!! And rook must stay on 2!!!
Playing optimally does not mean delay mate as long as possible but to try to maximize the outcome of the game. Here that would mean capturing the rook to achieve a draw. But if black also assumes white is rational, he knows he has already lost so either choice goes for them, they all have the same value, -1 (a game loss).
Log in to reply
-1 is not a game loss -10 or above is
Log in to reply
I mean -1 as in 1 is a win, 0 a draw, -1 a loss. Combinatory min max tree value. Not the score of the pieces.
Log in to reply
@Orlando Moreno – Black will never get the opportunity to capture the rook, since we as white are playing to win.
I forgot chess typing since I haven't done it in too long. But I can't see the mate in 3 while the mate in 5 is definite. 1-White king moves left. Black moves left. 2- white king left again. Black right. 3- rock left moving away. Now a possible mate if black moves left but logically extending it moves right. 4- white king right. Now black is forced to move left facing the white king. 5- rock down checkmate.
Log in to reply
- White King left, Black King left.
- Rook moves up the rank to any square, Black King moves right
- Rook moves to the bottom of the board, checkmate.
Log in to reply
If black is playing optimally it should be mate in 5 moves.!
The black king can then move towards the rook
Log in to reply
@Manu Mehta – What's the point of doing that? If you're in check you're supposed to remove the threat. In this case, there's no way to get out of the way. Hence, a checkmate.
The problem is asking for the minimum number of moves for White to checkmate Black . Black can no longer make a move since it's a checkmate. Even if Black can (which doesn't make sense), it's irrelevant to what the problem is asking.
true.. somehow i didn't see it. thanks
if u move king towards left it is acheckmate
It can be done in ONE move by white. White King to KN7 (down one, left one). White king can make that move because it is not in danger, as taking it would be an illegal move for black. Please help me understand if I'm wrong.
Log in to reply
THE MOVE YOU ARE SAYING IS ILLEGAL AS YOUR KING WOULD BE IN CHECK
Exactly..why is that not a correct answer
The king IS in danger on g2. It is the king that "dies" first that loses. And black's king gets the first shot as its his turn after you move. After the white king has died all his pieces immediately surrender, and the black king would never be in any risk...
More formally, it is never allowed to capture the opponent's king. But having the option to do so means the opponent played an illegal move: Kg2 is not allowed.
mate in three is still avoidable cuz after Re1 the black still has Rf2 where none is protecting
Log in to reply
The white king is in g3. There's nowhere the black king can go.
Let the white rook be E2 and the white king be H3.
Let the black king be G1.
White King H3 to G3
Black King G1 to F1
White Rook E2 to E4
Black King F1 to G1
White Rook E4 to E1
I didn't get that far. I moved white once and black once and realized the black only has 1 move left and clicked the 3 for my answer :D
Best part of logic is you don't have to prove anything to get the right answer :D
Log in to reply
Yeah, I didn't think that far.
It's important to back the rook up. Otherwise the king can capture it. And it's important that he move along the E column and not the 2 row. Otherwise the king would have more move possibilities.
This notation is way easier to follow.
- kg3:kh1 2. re3:kg1(k cant move any of e, h2 or g2. so the only option g1). 3. re1##
Why can't white king move above black king? Black king would have nowhere to go without being in check, right? (Sorry--I don't understand notation.)
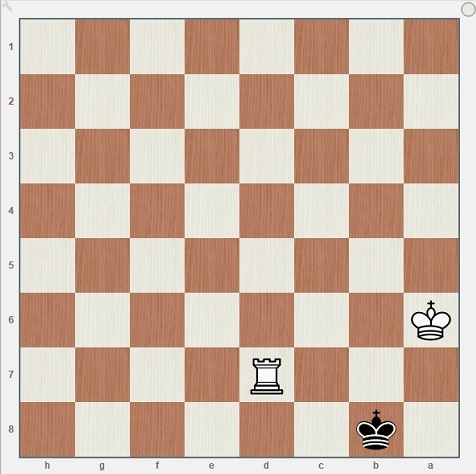Consider my diagram. The first move for white is Kb6. Then black answers with Kc8. Then white can play Rd6 or Rd5 or Rd4 or Rd3 or Rd2 or Rd1. Then the only move for black is Kb8. The final move for white is Rd8# for the checkmate. It is a mate in 3 puzzle.
There's no reason the Black King can't be on White's side of the board (the bottom). a1 is usually the lower left square in any diagram so White's side is on the bottom. Then it's just 1. Kg3 Kf1 2. Re3 (or 4-8, a waiting move) Kg1 3. Re1 mate. If 1. .... Kh1, 2. Re1 mate
Umm I know it's been a while since I played chess but I thought a king could move one space at a time in any direction (unless castling), so on your diagram (assuming it's whites go) if they move Kb7 it's mate in 1 move! Black can't take the white king cause it's guarded by the castle and can't move away cause it'll be taken no matter where it goes, or am I missing something?
It's a 3-move mate, as many people have said. But the question setters have turned the board through 90 degrees from the conventional representation. Conventionally, starting at bottom left, the algebraic representation has the columns marked a to h, and the rows marked 1 to 8. Any square is then identified by its column and row. For example bottom left is a1, bottom right is h1, top left is a8, etc. The other requirement is that a1 is a dark square, and consequently h1 is a light square.
In the problem, therefore, the dark square at bottom right is either a1 or h8, depending on which way they've turned the board.
In the first case, the white king is on c1, the white rook is on b4, and the black king is on a2. A 3-move solution is:
- Kc2 Ka3
- Rc4 Ka2
- Ra4 mate
In the second case, the white king is on f8, the white rook is on g5, and the black king is on h7. A 3-move solution is:
- Kf7 Kh6
- Rf5 Kh7
- Rh5 mate
In both cases there are 5 other suitable squares available to the rook on the second move, of course.
No need to rewrite the solution. Just turn the board 90 degrees.
Mate in one is evidently impossible. Mate in two can occur if
However, since black is playing optimally black will try to extend the mate as long as possible
The mate in three is unavoidable.