Fermat’s Sandwich
In the 17th century, French mathematician Pierre de Fermat challenged his colleagues with a variation of this question:
26 is an integer that is one more than a perfect square and one less than a perfect cube. Find another integer that has this property.
Does another integer like this exist?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
@Mark Hennings Sir, I knew about Mordell equations so I could solve this question....... But, could you please suggest me any good books for learning number theory in general???
Log in to reply
@Mark Hennings Sir??
Log in to reply
It all depends on what branch of Number Theory you want to study. Baker's "A Concise Introduction to Elementary Number Theory" is a good start, and cheap.
To understand my proof, you need to read more widely in algebra, and learn about rings, and in particular Euclidean domains, The books I learned this from are all rather old now (as am I), such as Herstein's "Topics in Algebra".
Log in to reply
@Mark Hennings – @Mark Hennings Right sir, thanks for the suggestion!!!!
Nice write-up!
Didn’t understand a word of it..
why 8 can't devide a²+2 ?
Log in to reply
A square is congruent to either 0 or 1 or 4 modulo 8 . Thus a 2 + 2 is congruent to either 2 or 3 or 6 modulo 8 , so cannot be a multiple of 8 .
For that matter, a 2 + 2 is congruent to either 2 or 3 modulo 4 , so is not even a multiple of 4 .
32768^2=1073741822, while 1024^3=1073741824 the answer is yes
Log in to reply
I am afraid not. 3 2 7 6 8 = 2 1 5 , while 1 0 2 4 = 2 1 0 , and so 3 2 7 6 8 2 = 1 0 2 4 3 = 1 0 7 3 7 4 1 8 2 4 . The square and the cube are equal, and do not differ by 2 .
A number base 10 ending in 8 squared must end in 4, not 2.
2 powers of 2 never differ by 2 except for 2 and 4
32768^2=1073741824
HOW IS THIS QUESTION EVEN LEVEL 1!
Beautiful, thank you for this.
a^2 + 2 = b^3 There are two possibilities: that both numbers are even or that they are odd.
Pair option:
a = 2K;
b = 2M;
(2k)^2 + 2 = (2M)^3;
4k^2 + 2 = 8M^3;
2k^2 + 1 = 4M^3 -> that's impossible because both 2k^2 and 4M^3 are even.
Odd option:
we take a^2 = 2K + 1, and b^3 = 2 (K + 1) +1
From the first equation:
a^2 - 1 = 2K;
(a+1) (a-1) = 2K;
Both (a+1) and (a-1) must be even, so K must be even.
From the second equation:
b^3 - 1 = 2(K+1);
(b-1) (b^2 +b+1) = 2(K+1);
Since K is even, (K+1) must be odd.
Therefore, either (b-1) = 2, or (b^2 + b+1) = 2.
Obviously the only possibility is that (b-1) = 2 -> b = 3, and there are no more possibilities.
Log in to reply
For your line (b - 1) = 2 or (b^2 + b + 1) = 2, couldn't you also have b - 1 be any odd number times two? For example, I don't think you ruled out the possibility that b = 7 in that step (because (7 - 1)(7^2 + 7 + 1) = 2 * 171).
I agree with David. If K + 1 is odd, you are saying that b 3 − 1 is congruent to 2 modulo 4 . This means that b 3 is congruent to 3 modulo 4 . But this is true whenever b is congruent to 3 modulo 4 .
Log in to reply
You are absolutely right. As I have already indicated, my reasoning is wrong.
It seems to be solvable with intuition. The gap between higher squares and cubes will be bigger, whereas the gap between smaller ones will be smaller. Therefore a gap of exactly 2 won't happen again.
you're wrong. you didn't even understand the question
Log in to reply
To expand on that, I think you are thinking in terms of some function of a single variable compared to another function of the same variable. Even in the example (I.e. the only solution) the square and cube had different bases.
It's not correct. Think that 4096 is both a perfect square and a cube.
not the gap bethween any square and any cube
You didn't think that one all the way through. 64 is a perfect cube and a perfect square. The numbers being cubed and squared do not necessarily have to be close to each other.
Look who got the answer correct by chance!
0 is one more than the (-1)^3 & (1)^2
You're only considering n^2 to n^3 relations. Think of it this way. 25 and 27 are 2 apart, but 125 and 121 are only 4 apart. The gap doesn't keep getting bigger. It reaches 0 with numbers like 64.
Beware the law of small numbers!
When you look at x^2 and x^3 and the difference between such, you are assuming the same x, the question asks for any number. Based on the logic you proposed, a solution of 26 wouldn't have been deduced.
27^2=9^3, zero is technically a smaller gap than 2.
Also, the difference between different squares and cubes rises and drops. 0^2 - 1^3 = -1
0^2 - 2^3 = -8
1^2 - 0^3 = 1
1^2 - 2^3 = -7
2^2 - 0^3 = 4
2^2 - 1^3 = 3
2^2 - 2^3 = -4
3^2 - 0^3 = 9
3^2 - 1^3 = 8
3^2 - 2^3 = 1
3^2 - 3^3 = -18
4^2 - 0^3 = 16
4^2 - 1^3 = 15
4^2 - 2^3 = 8
4^2 - 3^3 = -11
5^2 - 0^3 = 25
5^2 - 1^3 = 24
5^2 - 2^3 = 17
5^2 - 3^3 = -2
6^2 - 2^3 = 28
6^2 - 3^3 = 9
6^2 - 4^3 = -28
7^2 - 3^3 = 22
7^2 - 4^3 = -15
9^2 - 4^3 = 17
10^2 - 5^3 = -25
11^2 - 5^3 = -4
12^2 - 5^3 = 19
14^2 - 6^3 = -20
15^2 - 6^3 = 9
18^2 - 7^3 = -19
19^2 - 7^3 = 18
22^2 - 8^3 = -28
23^2 - 8^3 = 17
32^2 - 10^3 = 24
47^2 - 13^3 = 12
58^2 - 15^3 = -11
70^2 - 17^3 = -13
181^2 - 32^3 = -7
207^2 - 35^3 = -26
225^2 - 37^3 = -28
253^2 - 40^3 = 9
282^2 - 43^3 = 17
312^2 - 46^3 = 8
375^2 - 52^3 = 17
1138^2 - 109^3 = 15
378661^2 - 5234^3 = 17
736844^2 - 8158^3 = 24
For i^2-ii^3=n, where i<10^6, -30<n<30, n<>0
The way I solved is rather elementary but a bit long. Here goes the solution: First, note that the problem is equivalent to finding integer solutions of the equation y 3 − x 2 = 2 . Now, note that, obviously, y has to be a positive integer. Also, note that both ± x are solutions of the equation when x is a solution. So we will focus on finding solutions ( x , y ) ∈ Z + × Z + . Since y ≥ 1 , note that x cannot be smaller than y , as otherwise, x = y − a for some a ≥ 0 , which would imply y 3 − x 2 = y 3 − ( y − a ) 2 , which is an increasing function of a (as y − a ≥ 0 ), and has the minimum value y 3 − y 2 , which is 0 for y = 1 , and ≥ 4 for y ≥ 2 . Thus, we must have x = y + a , for some a ≥ 1 . Now, the equation becomes y 3 − ( y + a ) 2 = 2 ⟹ ( y 3 − 3 3 ) = ( y + a ) 2 − 5 2 ⟹ ( y − 3 ) ( y 2 + 3 y + 9 ) = ( y + a + 5 ) ( y + a − 5 ) . Now,observe that it is not possible for both y + a + 5 and y + a − 5 to be simultaneously divisors of y 2 + 3 y + 9 , because otherwise, we would have y = 4 , which does not satisfythe equation for any a ≥ 1 . Thus, we must have y + a − 5 ∣ y − 3 , since y + a + 5 ∣ y − 3 is not possible as a ≥ 1 . Thus, we have a ≤ 2 . Now, for a = 1 , we have y − 4 ∣ y − 3 which is not possble as y − 4 , y − 3 are relatively prime. Thus, we must have a = 2 , which yields ( y − 3 ) ( y 2 + 3 y + 9 ) = ( y + 7 ) ( y − 3 ) ⟹ ( y − 3 ) ( ( y + 1 ) 2 + 1 ) = 0 ⟹ y = 3 . Thus the only solutions are ( x , y ) = ( ± 5 , 3 ) . □
E D I T : As pointed out by @Mark Hennings , my proof has a serious gap, which makes it far from correct. I would try to make it complete by removing the flaw. However, I am beginning to think that finding an elementary way to do so might be a real challenge.
But why (y + a - 5) devides y-3. ???
This is a good attempt, but there are some problems with it. One minor, one major.
If both y + a − 5 and y + a − 5 divide y 2 + 3 y + 9 , then y − 3 must divide 1 . This means that it is possible that y = 2 , with y − 3 = − 1 , as well as the case y = 4 you consider. It is easy to exclude the case y = 2 , so this is not a big problem.
The big problem is that you are assuming that y + a + 5 must divide either y − 3 or y 2 + 3 y + 9 . It is possible that neither is true. Just because p q = r s for integers p , q , r , s does not mean that r divides either p or q . Consider the case 1 2 × 1 8 = 8 × 2 7 . Then 8 divides the product 1 2 × 1 8 without dividing either 1 2 or 1 8 .
OK, it is not possible for y + a + 5 to divide y − 3 . However, a factor of y + a + 5 could divide y − 3 , which is a case you have not considered, and this would mean that it was not necessary for y + a − 5 to divide y − 3 . There is quite a bit of work to do to plug this gap.
Log in to reply
Is there any other solution to this @mark? I mean an elementary one which do not involve complex algebra.
Log in to reply
The problem was originally set by Fermat as a challenge to his colleagues. He never wrote down his proof (again), but it is assumed that he thought it could be proved by his method of infinite descent. The proof I gave is the standard one, and is due to ideas of Euler. I don’t think I have ever seen a first principles proof...
Hi @Mark Hennings , thanks for pointing out this major gap in the proof. I will definitely try to fill this gap and make it complete.
Your graph works if the question was restricted to a = b , but you also have to consider all possible positive integers for a and b . In other words, you would also have to consider the graphs y 1 = ( a + m ) 2 + 2 and y 2 = ( b + n ) 2 + 2 for all integers m and n such that a + m > 0 and b + n > 0 .
that isn't a right solution
If a smart guy challanges other smart guys to find another then chances are he already did the math and diddnt find any... smart nose tap
If we see the graph of both the functions y=x^2 +1 & y=x^3 -1, we will analysis that they will intersect at only at 26 and will never intersect
What intersection a=5,b=3 a not equal to b ,stupid fool.
Sorry, for the wrong comment, actually I was trying to state that if we analyse their graph they will intersect at 1 only & will never intersect Thanks for Finding Flaw.
I didn't really try to prove it, just figured that Fermat was a troll 😂
Great Solution!
if you think deeper into the situation and then sum it up for other souls to understand, the perfect square is 25 from 5 Squared. One more than that is 26. It is also one less than a perfect cube as 3 cubed is 27 and only 3 cube can give 27. It is impossible for any other number to give this outcome because each number can only give one fixed number that is displayed. sounds complicated but you can think of it however u want as long as you understand the concept.
Haha good joke
Solve following two Diophantine equations using WolframAlpha
n-m^2=1,
k^3-n=1,
gives n=26, m=5 and k=3 as the only possible solution. Therefore, answer is NO.
This is an invalid answer.
Log in to reply
To be cheating, you would have to have agreement on the rules, so that's at least a debatable assertion.
However, it is definitely invalid unless you at least know what algorithm Wolfram Alpha is using to solve it. In the worst case (but also the most probable), WolframAlpha is just changing it into the system { k 3 − m 2 = 2 n = m 2 + 1 and then looking up the known solutions to k 3 − m 2 = d for d = 2 in a database. I.e. This answer would just be begging the question.
No but there is an integer which 1 more than a cube and 1 less than a square
Pls don't post such useless answers
I think I found the direction from which an easier, elementary solution could be found.
So, obviously x 2 + 1 = y 3 − 1 . We want to show that "26" is the only solution, that is, the number that equals both sides.
So I had the idea to takeaway 26 from both sides so the new equation would have to equal 0 both sides. That would give new opportunities, as you could for example prove with "infinite" prime factorization and finding an infinite chain of primes which divide both sides etc. So x 2 − 2 5 = y 3 − 2 7 . Thus ( x − 5 ) ( x + 5 ) = ( y − 3 ) ( y 2 + 3 y + 9 ) and you could see some solutions. So I wanted to prove that x = 5 , y = 3 so I used k = x − 5 , l = y − 3 and thus k ( k + 1 0 ) = l ( l ( l + 9 ) + 2 7 ) and again tried to find some primes that divide both sides. For example, 2 surely divides both k , l . Also noted that whereas if they equal a number M, k is relatively close to M , whereas l\( should be a small divisor, but \(M/l\( is exactly bigger by 27 of a multiple of \(l\(. Thus you could show that if \(k=2^mn\(, then \(2^{m+1}|l which makes (n( really big. I didn't advance much from this, but I see good.
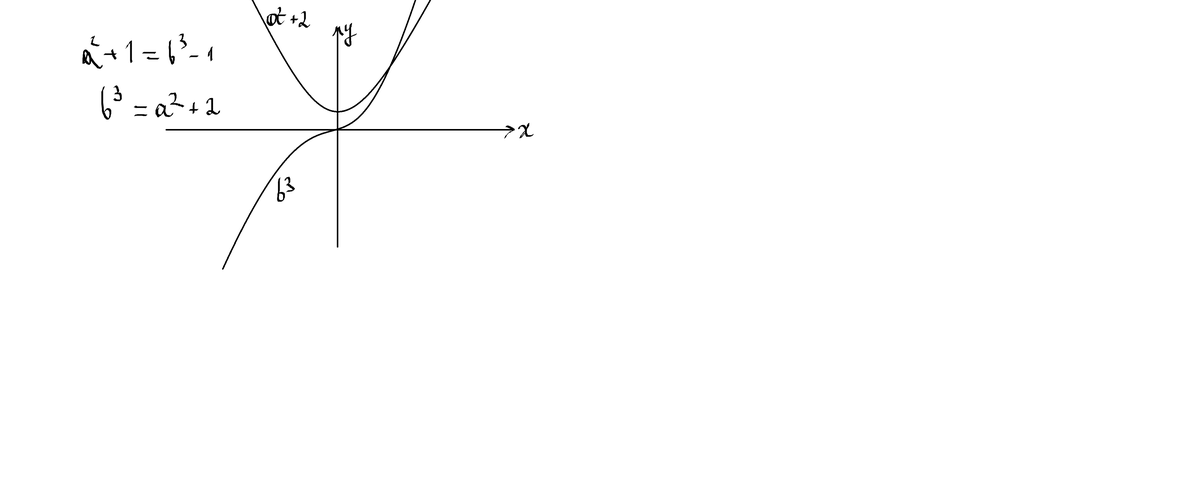
This, of course, is one case of Mordell's equation.
Suppose that a , b ∈ Z are such that a 2 + 1 = b 3 − 1 , so that b 3 = a 2 + 2 . If a were even, then b would be even, which would mean that 8 divided a 2 + 2 , which is not possible. Thus a is odd.
We can factor b 3 = ( a + i 2 ) ( a − i 2 ) in the Euclidean domain Z [ i 2 ] (the distance function is N ( a + i b 2 ) = a 2 + 2 b 2 ). If u ∈ Z [ i 2 ] is a common factor of a + i 2 and a − i 2 , then u divides their difference 2 i 2 , and hence N ( u ) divides N ( 2 i 2 ) = 8 . On the other hand, N ( u ) also divides N ( a + i 2 ) = a 2 + 2 , which is odd. Thus N ( u ) = 1 , and hence u is a unit in Z [ i 2 ] . Since ( a + i 2 ) ( a − i 2 ) = b 3 is a perfect cube in Z [ i 2 ] and since a + i 2 and a − i 2 are coprime, we deduce that a + i 2 is equal to a cube in Z [ i 2 ] times a unit in Z [ i 2 ] . Since the units of Z [ i 2 ] are ± 1 , both of which are cubes, we deduce that a + i 2 is a cube in Z [ i 2 ] . Thus a + i 2 = ( p + i q 2 ) 3 for some integers p , q , so that a = p ( p 2 − 6 q 2 ) 1 = q ( 3 p 2 − 2 q 2 ) Looking at the second equation, q = ± 1 . If q = − 1 we must have 3 p 2 = 1 , which is impossible. Thus q = 1 , and so 3 p 2 = 3 , so that p = ± 1 . This implies that a = ± 5 , which implies that b = 3 .
Thus the only solutions in integers to the equation a 2 + 1 = b 3 − 1 are a = ± 5 , b = 3 , and so the desired number is 2 5 + 1 = 2 7 − 1 = 2 6 .