Fibonacci Function

We can split up the function into 6 pieces, one for each example given. It's easy to see that the polynomial is

$\dfrac{1}{15}(x-1)(x-2)(x-3)(x-4)(x-5)-\dfrac{5}{24}(x-1)(x-2)(x-3)(x-4)(x-6)$ $+\dfrac{1}{4}(x-1)(x-2)(x-3)(x-5)(x-6)-\dfrac{1}{6}(x-1)(x-2)(x-4)(x-5)(x-6)$ $+\dfrac{1}{24}(x-1)(x-3)(x-4)(x-5)(x-6)-\dfrac{1}{120}(x-2)(x-3)(x-4)(x-5)(x-6)$

This is kind of like applying Chinese Remainder Theorem on a polynomial! For example, watch what happens when we plug in 6. The first "term" is 8 which all the other "terms" are 0 because they contain an $(x-6)$ .

Evaluating this at $x=7$ we get $\boxed{8}$ .

The difference construction is a simple yet elite way to solve this. In this method, one draws a table with the values ( f(x) ), D(1), D(2)...uptil D(n) where D(n) indicates the degree of the polynomial. Using the binomial theorem one can also prove that D(n) is always constant. The D(1) here indicates the difference between two consecutive f(X)'s. Similarly D(2) indicates the difference between two consecutives D(1). Thus doing uptil D(5) ..we obtain a relation between the functional results of the polynomial. We find that using the fact D(n) is useful and continue to draw tables backward till D(1) and obtain that difference between f(7) and f(6) is 0. Thus f(7) =8. Whew! :)... SORRY, I didnt know to type this out in LaTeX. My apologies

$\textbf{NOTE}$ - I just have understood the solution given by Krishna Ar and made a table for it as the problem writer couldn't make a table. This Solution is $\textbf{not mine}$

$\begin{array}{c|c|c|c|c|c}f(x) & D_{1} & D_{2} & D_{3} & D_{4} & D_{5}\\\hline 1\\\hline 1 & 0\\\hline 2 & 1 & 0\\\hline3 & 1 & 0 & -1\\\hline5 & 2 & 1 & 1 & 2\\\hline8 & 3 & 1 & 0 & -1 & -3\\\hline f(7) & 0 & -3 & -4 & -4 & -3 \\\hline \end{array}$

Hence, $f(7) = 8$

First define the polynomial $g(x) = f(x+1) - f(x)$ . We easily get that $g(1) = 0, g(2) = g(3) = 1, g(4) = 2,$ and $g(5) = 3$ .

Now define $h(x) = g(x+1) - g(x)$ , so that $h(1) = h(3) = h(4) = 1$ and $h(2)=0$ .

Now we must have for some constant $c$ that $h(x) = c(x-1)(x-3)(x-4)+1$ , since the polynomial $h(x)-1$ has roots at $x=1,3,4.$ .

Of course, we also have $h(2) = 0$ , which means that $c=-\frac{1}{2}$ .

Now we simply have $f(7) = f(6) + g(6) = 8+g(6)=$ $=8+g(5)=h(5) =$ $= 11 + 1 -\frac{1}{2}\cdot (5-1)(5-3)(5-4) = 12 - 4 =8.$

The definition of a quintic polynomial is $f(x) = ax^5+bx^4+cx^3+dx^2+ex^1+f$

in our case

$f(1)=a*1^5+b*1^4+c*1^3+d*1^2+e*1^1+f = a + b + c + d + e + f = 1$ $f(2)=a*2^5+b*2^4+c*2^3+d*2^2+e*2^1+f = 32a + 16b + 8c + 4d + 2e + f = 1$ $f(3)=a*3^5+b*3^4+c*3^3+d*3^2+e*3^1+f = 243a + 81b + 27c + 9d + 3e + f = 2$ $f(4)=a*4^5+b*4^4+c*4^3+d*4^2+e*4^1+f = 1024a + 256b + 64c + 16d + 4e + f = 3$ $f(5)=a*5^5+b*5^4+c*5^3+d*5^2+e*5^1+f = 3125a + 625b + 125c + 25d + 5e + f = 5$ $f(6)=a*6^5+b*6^4+c*6^3+d*6^2+e*6^1+f = 7776a + 1296b + 216c + 36d + 6e + f = 8$

We got 6 linear equations with 6 variables.

Solving -

$a=-\frac{1}{40}$ $b=\frac{11}{24}$ $c=-\frac{25}{8}$ $d=\frac{241}{24}$ $e=-\frac{287}{20}$ $f=-8$

and now

$f(7)=a*7^5+b*7^4+c*7^3+d*7^2+e*7^1+f = 16807*-\frac{1}{40} + 2401*\frac{11}{24} + 343*-\frac{25}{8} + 49*\frac{241}{24} + 7*-\frac{287}{20} - 8 = \boxed{8}$

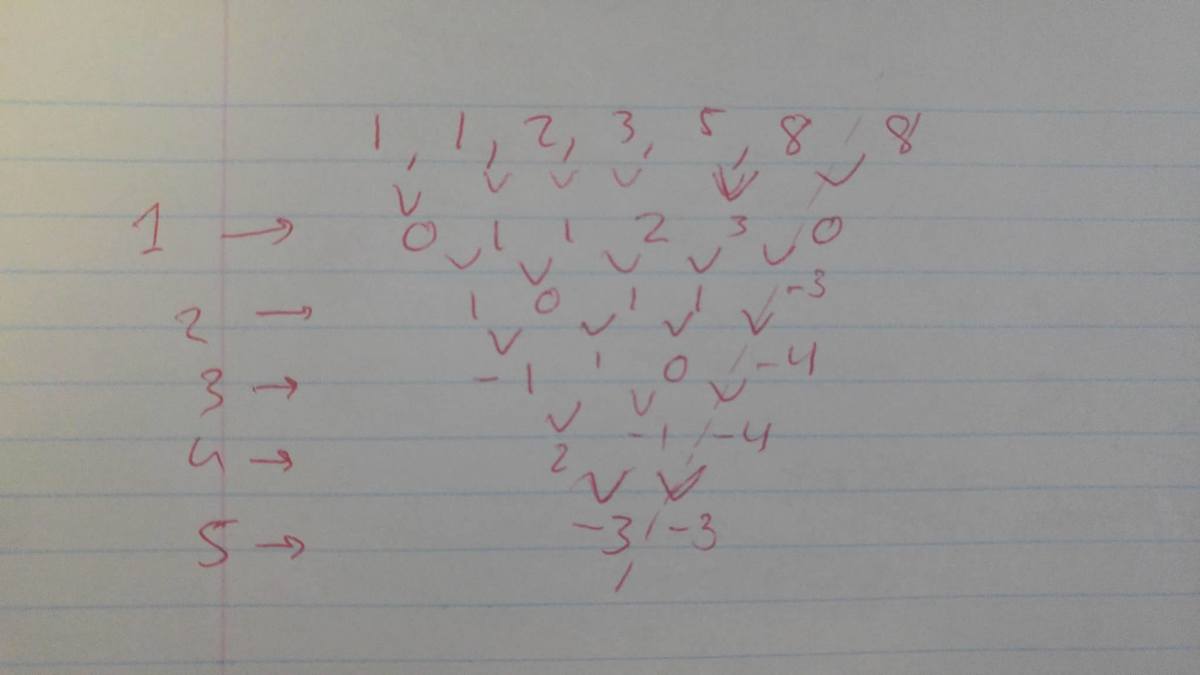
Since the 5th difference will be constant.

Lagrange interpolation gives $f(x) = -\frac1{40}x^5 + \frac{11}{24}x^4 - \frac{25}8x^3 + \frac{241}{24}x^2 - \frac{287}{20}x + 8$ , so $f(7) = 8$ . Not the most elegant solution!

Let $f_5(x)=ax^5+bx^4+cx^3+dx^2+ex+f$ . Notice that if we let $f_4(x) = f_5(x+1) - f_5(x)$ , then $f_4$ is a fourth degree polynomial. Again, let $f_3(x) = f_4(x+1) - f_4(x)$ , so $f_3$ is a third degree polynomial. We continue doing this until and define $f_0$ which is a constant function (or 0th degree polynomial).

Now, we know $f_5(1)...f_5(6)$ so we can easily find $f_4(1)...f_4(5)$ , and then we can find $f_3(1)...f_3(4)$ and so on. We eventually find that $f_0(1) = -3$ . But, since $f_0$ is a constant function, $f_0(2)$ must also be $-3$ . Using that, we can calculate $f_1(3)$ , which we didn't before because we only know $f_1 (1), f_1(2)$ . Then, working out way back up, we can easily calculate $f_5(7)$ .

In a diagram, this looks like:

$f_5$ 1 1 2 3 5 8 8

$f_4$ 0 1 1 2 3 0

$f_3$ 1 0 1 1 -3

$f_2$ -1 1 0 -4

$f_1$ - 2 -1 -4

$f_0$ -3 -3

The Fibonacci numbers are just there to trick you! In fact, if you were to construct a 6th degree polynomial with f(1)...f(7) equal to 1,1,2,3,5,8, and 13, I bet you f(8) will not be 21.

<p> I will integrate the solution with a general method. </p> <p> When you have a polynomial of degree $n$ with $n+1$ fixed values, the polynomial is fixed too. There are mainly three ways to work out the polynomial: </p> <p> 1) By hand . If $p(a) = y$ , then <br /> </p> <p> $p(x) = y+ (x-a) q(x)$ <br /> </p> <p> for some polynomial $q(x)$ such that $\deg q = \deg p -1$ . If you put the values you know into the polynomial you'll gradually construct it. <br />
</p> <p> 2) Lagrange formula . Suppose you know that <br /> </p> <p> $p(x_i) = y_i$ , for $i=0, \ldots, n$ .<br /> </p> <p> We want to costruct some polynomials $p_i(x)$ for $i=0, \ldots, n$ such that ( divide et impera method): <br /> </p> <p> $p_i(x_i) = 1$ and $p_i(x_j) = 0$ for every $j \neq i$ . <br /> </p> <p> We note that <br /> </p> <p> $\displaystyle p_i(x) = \prod_{j \neq i} \frac{ (x-x_j) }{ (x_i -x_j)}$ <br /> </p> <p>is exactly what we were searching for. So our $p(x)$ is (why?) </p> <p> $\displaystyle p(x) = \sum_{i=0}^n y_i p_i(x) = \sum_{i=0}^n \prod_{j \neq i} \frac{ (x-x_j)}{(x_i-x_j)}$ </p> </p> <p> 3) Finite difference polynomials . Let's define, for every polynomial $p$ : </p> <p> $p_i(x) = p_{i-1}(x+1)-p_{i-1}(x)$ , where $p_0(x) = p(x)$ . </p> <p> You can easily check that $\deg p_{i+1} = \deg p_i - 1$ if $\deg p_{i+1} > 0$ . This means, by induction, that $\deg p_i =n -i$ for $i=0, \ldots, n$ , where $n= \deg p$ , i.e. $p_n(x)$ is constant. </p> <p>This observations are not enough to work out to polynomial, but allow to find other values of the polynomial.
</p> <p>Suppose you know that $p(i) = y_i$ for $i=0,\ldots, n$ . <br /> </p> <p>Let's construct the FDA (finite difference array) in this way: </p> <p> LINE 1: $p(0), \ \ \ \ldots \ \ \ , p(n)$ </p> <p> LINE 2: $\ \ p_1(0), \ \ \ldots \ \ , p_1(n-1)$ </p> <p> .. </p> <p> LINE $i+1$ : $p_i(0), \ \ \ldots \ \ , p_i(n-i)$ <br /> </p> <p> .. </p> <p> LINE $n+1$ : $p_n(0)$ </p> <p> Now, using the fact that $p_n$ is constant, you can find the value of $p(n+1)$ by going from the bottom to the top of the pyramid. </p> <p> A little bit more. There is a way to work out the polynomial with FDA. Let's call $c_i = p_i(0)$ . We claim that </p> <p> $\displaystyle p(x) = \sum_{i=0}^n c_i \binom{x}{i} (*)$ </p> <p> where $\displaystyle \binom{x}{k} = \frac{ x \cdot \ldots \cdot (x-k+1)}{k!}$ . </p> <p> If $\displaystyle q(x) = \binom{x}{k}$ ,you can easily verify that $\displaystyle q_i(x) = \binom{x}{k-i}$ for $i=0, \ldots, k$ using the fact that $\displaystyle \binom{x+1}{k} - \binom{x}{k} = \binom{x}{k-1}$ , and 0 if $i>k$ . Then we can verify that (*) holds by demonstrating that $p_i(0) = c_i$ : </p> <p> $\displaystyle p_i(0) = \sum_{j=0}^n c_j \binom{0}{j-i} = c_i$ </p> <p> because $\binom{0}{i}$ is 0 if $i \neq 0$ and 1 if $i=0$ . </p> Aargh, this is the less professional place where to write math. I can't find a newline command which preserve latex (as markdown doesn't do). Can you help me?

A straightforward application of Lagrange Interpolation Formula .

Here is a solution requiring moderate algebra, somehow intermediate between the 6 variable equation resolution, and the more clever solutions presented in other comments (with finite differences of f).

We can notice that this category of problem usually involves finding a function which has the same value as f on the given points.

The simplest (linear) function that we can quickly identify is

$g(x) = x - 1$

g equals f on $x = 2, 3, 4$ such that if

$h(x) = f(x) - g(x)$

Then h can be written :

$h(x) = (x-2)(x-3)(x-4)P(x)$

Where $P[X]$ is a polynom of degree 2.

Solving P for $x = 1, x = 5, x = 6$

We find:

$P(x) = \frac{-1}{40} x^2 + \frac{7}{30} x + \frac{-9}{24}$

And the exact expression for f

$f(x) = (x-2)(x-3)(x-4) (\frac{-1}{40} x^2 + \frac{7}{30} x + \frac{-9}{24}) + (x-1)$

With F(x) = a x^5 + b x^4 + c x^3 + d x^2 + e x + f, joining (1, 1), (2, 1), (3, 2), (4, 3), (5, 5), (6, 8) and finding (7, ?). Substitutes all points to function to form 6 simultaneous equations of 6 unknowns namely a, b, c, d, e and f. Solve by Cramer's formulation for evaluating seven 6 x 6:

D = -34560;

Da = 864 => a = -0.025;

Db = -15840 => b = 0.4583333+;

Dc = 108000 => c = -3.125;

Dd = -347040 => d = 10.0416666+;

De = 495936 => e = -14.35;

Df = -276480 => f = 8;

Therefore F(7) = 8. We can draw and observe. You would appreciate the curve. {The 'f' is taken as constant while replaced with 'F'.} Quintic curve is not suitable for interpolation for Fibonacci Function outside its actual range. Nevertheless, non-integers in between are good.

Let f(x) =ax^5+bx^4+cx^3+dx^2+ex+f, and evaluate in x=1,2...6. You will have a 6x6 system. Solve it and you will get the coeficients of f(x), Then evaluate f(7)=8

There is a very long, convoluted process that you can perform using row reduction , or, more specifically, Gaussian elimination. If one has ever tried applying linear algebra to solve giant systems of linear equations, using and simplifying augmented matrices using Gaussian elimination is a safe and easy, but very complicated, way to go about solving problems like these.

First of all, the general form of a quintic function is $f(x) = Ax^5 + Bx^4 + Cx^3 + Dx^2 + Ex + F$ . The coefficients, A , B , C , D , E , and F , are what we do not know and wish to solve for, and, fortunately, we are given six inputs and outputs of the function, and we have six unknowns. This means that we can set up a system of six linear equations in six unknowns.

However, to compact our system into a more reasonable space, we can put the coefficients of the unknowns (which you get by substituting the function arguments given in the problem for where there is an x ) inside an augmented matrix. Then, using Gaussian elimination, the row echelon form of the initial matrix is

The row reduction process takes 21 steps, most of which have been omitted to just the original matrix and the final matrix in row echelon form. Try this on your own if the details seem hazy to you.

If one does not know linear algebra and is not comfortable with Gaussian elimination, I would not recommend that one use this approach, but it is a much faster method than using the elimination method of linear combination for solving linear systems of equations.

Could not think of a way so I solved it in MATLAB :P

A=[ 1 1 1 1 1 1 ; 2^5 2^4 2^3 2^2 2^1 1; 3^5 3^4 3^3 3^2 3^1 1; 4^5 4^4 4^3 4^2 4^1 1;5^5 5^4 5^3 5^2 5^1 1;6^5 6^4 6^3 6^2 6^1 1];

b=[1;1;2;3;5;8];

x=inv(A)*b;

x(1) 7^5+x(2) 7^4+x(3) 7^3+x(4) 7^2+x(5)*7+x(6) %=8

Lagrange interpolation was of course the solution but I did not come up with it by myself.

I think that it would be better to have this as some logical sequence, than a math problem (well it would be an easy logic test btw)

f(x+1)-f(x)=a(x-5)(x-4)(x-3)(x-b) , where a,b are constants. input x=2,1 to determine a,b and we get a=-1/8,b=2/3. At the end, input x=6