Fibonacci-Geometric Progression!
1 0 1 + 1 0 2 1 + 1 0 3 2 + 1 0 4 3 + 1 0 5 5 + 1 0 6 8 + ⋯
Find the sum of the above fractions, where the denominators follow a geometric progression and the numerators follow the Fibonacci sequence .
If your answer is B A , where A and B are coprime positive integers, submit your answer as A + B .
The answer is 99.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
8 solutions
Awesome question and explanation I loved it, keep posting more, thanks!
This is great! (+1)
Unbelievable!
Simple and best
Brilliant!! Just loved the simplicity of how the series simplifies out.
Though, Fibonacci Sequence is generally defined by recursive relation, but it can also be defined explicitly using F n = 2 n ⋅ 5 ⋅ ( 1 + 5 ) n − ( 1 − 5 ) n , where n ϵ N . . . . . . . . . . . . . By Binet’s Fibonacci Formula .
Now, the given series is equal to ∑ n = 1 ∞ 1 0 n F n = ∑ n = 1 ∞ 1 0 n ⋅ 2 n 5 ( 1 + 5 ) n − ( 1 − 5 ) n . ⟹ 5 1 ⋅ ( n = 1 ∑ ∞ ( 2 0 1 + 5 ) n − n = 1 ∑ ∞ ( 2 0 1 − 5 ) n ) = 5 1 ( 1 9 − 5 1 + 5 − 1 9 + 5 1 − 5 ) = 3 5 6 5 4 0 5 = 8 9 1 0 . Hence a + b = 1 0 + 8 9 = 9 9 .
How did you simplify those summations inside the parenthesis from the second line of your solution?
Log in to reply
You can easily see that both the series are infinite geometric series whose common ratios lies between ( − 1 , 1 ) , they are ( 2 0 1 + 5 ≈ 0 . 1 6 1 ) and ( 2 0 1 − 5 ≈ − 0 . 0 6 1 ) . This means both the sums approaches a number which can be evaluated by using the formula 1 − β α , where α and β denotes, respectively, the first term and common ratio. Use this formula and you would be able to get the result.
Log in to reply
Ohhh... It was a silly mistake, didn't notice that the summation tends to infinity. Great job though!
The closed form for F n that you state is actually called the Binet's Fibonacci formula . Since you don't provide a proof yourself, you should at least provide a reference to it for the reader.
Log in to reply
Yes, you are right I should have proved it, but that would have made the solution unnecessarily lengthy. But anyways I'm editing the solution mentioning link for reference. Thanks for your advice.
This is a more or less a similar approach as @Manuel Kahayon used.
S 1 0 S S − 1 0 S 1 0 9 S ∴ S = 1 0 1 + 1 0 2 1 + 1 0 3 2 + 1 0 4 3 + 1 0 5 5 + 1 0 6 8 + … = 1 0 2 1 + 1 0 3 1 + 1 0 4 2 + 1 0 5 3 + 1 0 6 5 + 1 0 7 8 + … = 1 0 9 S = 1 0 1 + 1 0 0 S 1 0 3 1 + 1 0 4 1 + 1 0 5 2 + 1 0 6 3 + 1 0 7 5 + … = 1 0 1 + 1 0 0 S = 8 9 1 0 ⇒ 1 0 + 8 9 = 9 9
Yep... I also did the exact same way..... (+1)
Note that the generating function of the Fibonacci sequence is, f ( x ) = k = 1 ∑ ∞ F k x k = 1 − x − x 2 x
Hence, the given expression, is equal to f ( 1 0 1 ) = 8 9 1 0
Required answer = 9 9
Consider a polynominal that
x + x 2 + 2 x 3 + 3 x 4 + 5 x 8 ⋯ = A
Then
( x + x 2 + 2 x 3 + 3 x 4 + 5 x 5 + 8 x 6 ⋯ ) ( x + 1 )
= x + 2 x 2 + 3 x 3 + 5 x 4 + 8 x 5 + ⋯
= ( A − x ) / x
Therefore
A ( x + 1 ) = ( A − x ) / x
A x ( x + 1 ) + x = A
A ( x 2 + x − 1 ) = − x
∴ A = x 2 + x − 1 − x
In this problem, substitute 1/10 in x.
1 / 1 0 0 + 1 0 / 1 0 0 − 1 0 0 / 1 0 0 − 1 / 1 0
= 8 9 1 0
So the answer is 1 0 + 8 9 = 9 9 .
Let the sum be S , then we have S − 1 0 S = 1 0 1 + 1 0 0 S and solve for S
∑ n = 1 ∞ F n x n = 1 − x − x 2 x generating function
put x = 1 0 1
∑ n = 1 ∞ 1 0 n F n = 8 9 1 0
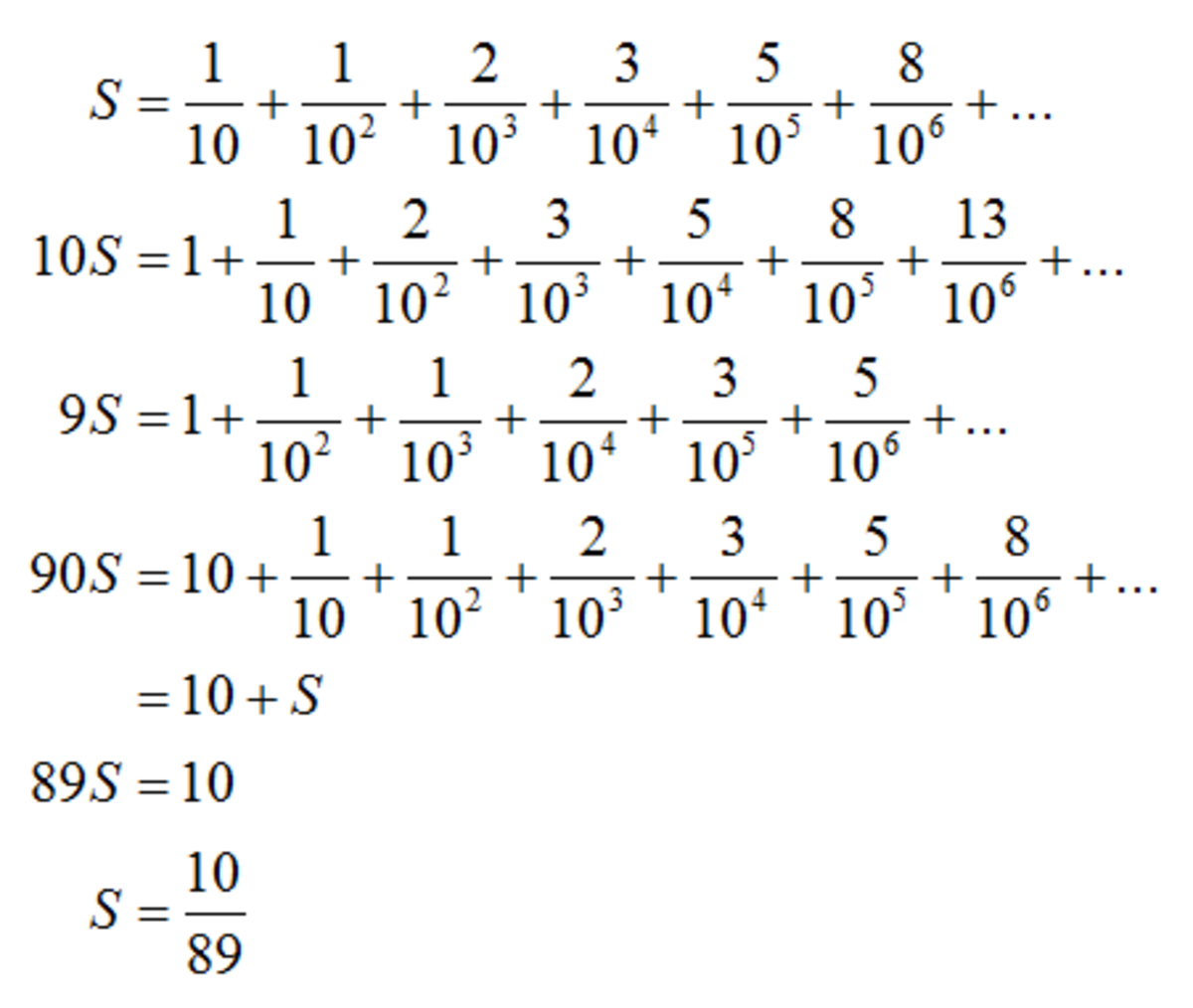
Let x = 1 0 1 + 1 0 2 1 + 1 0 3 2 + 1 0 4 3 + 1 0 5 5 + 1 0 6 8 + ⋯
1 0 x = 1 0 2 1 + 1 0 3 1 + 1 0 4 2 + 1 0 5 3 + 1 0 6 5 + 1 0 7 8 + ⋯
x + 1 0 x = 1 0 1 + 1 0 2 2 + 1 0 3 3 + 1 0 4 5 + 1 0 5 8 + ⋯
x + 1 0 x + 1 = 1 + 1 0 1 + 1 0 2 2 + 1 0 3 3 + 1 0 4 5 + 1 0 5 8 + ⋯
x + 1 0 x + 1 = 1 0 ⋅ ( 1 0 1 + 1 0 2 1 + 1 0 3 2 + 1 0 4 3 + 1 0 5 5 + 1 0 6 8 + ⋯ )
x + 1 0 x + 1 = 1 0 x
x = 8 9 1 0
So, our answer is 1 0 + 8 9 = 9 9