Fibonacci Remainder!

Number Theory Level 3

$1,1,2,3,5,8,13,21,...$

If we divide the terms in the Fibonacci sequence above by $2$ , then the remainders will be $1,1,0,1,1,0,1,1,0,...$ .
Obviously, the ratio of the numbers of $0$ s and $1$ s in the sequence goes to $1:2.$

If we divide the terms by $3$ , then the remainders will be $1,1,2,0,2,2,1,0,1,1,2,0,...$ .
The ratio of the numbers of $0$ s, $1$ s, and $2$ s in the sequence now goes to $2:3:3.$

Now, we divide the terms by a positive integer $n$ and obtain a sequence of remainders.
Then the ratio of the numbers of $0$ s, $1$ s, $2$ s, $\ldots,$ $(n-1)$ s in the sequence goes to $1:1:1:\ldots:1.$

What is the sum of all possible $\frac1n,$ if $n$ can also be 1?

Clarification: Each whole number smaller than $n$ has the same probability to appear in the sequence of remainders. This is also the reason that $n$ can also be $1$ .

The answer is 1.25.

4 solutions

Mark Hennings
Sep 16, 2018

It was proved in 1972 that the Fibonacci numbers are uniformly distrbuted modulo $n$ precisely when $n$ is a power of $5$ . Thus the desired sum is $\sum_{k=0}^\infty 5^{-k} \; = \; \boxed{\tfrac54}$

@X X Hello!!! Could you please tell me, from where do you get these AMAZING problems??? I would be grateful...!! @X X ????

Aaghaz Mahajan - 2 years, 8 months ago

@Aaghaz Mahajan Thank you! They are mostly original, and I got some of them from other books. (But sometimes after I posted an "original" problem, I discovered that someone had posted a similar problem already. Like this one )

X X - 2 years, 8 months ago

Oh yeah I remember that one!!! But if most of your questions are purely original, Hats off to you!!!!

Aaghaz Mahajan - 2 years, 8 months ago

@Aaghaz Mahajan – @X X P.S. Just being curious, would you suggest any names of those "other books" ???

Aaghaz Mahajan - 2 years, 8 months ago

@Aaghaz Mahajan – Books in Chinese...

X X - 2 years, 8 months ago

@X X – Ohhhh!!! I see.......No worries!!! But still, I'll be waiting for more of your amazing questions!!!

Aaghaz Mahajan - 2 years, 8 months ago

But one thing is not clear. How did he guess that this happens only when it is of the form 5^k. It is mysterious.

Srikanth Tupurani - 2 years, 8 months ago

Pau Cantos
Sep 26, 2018

This gives only way of reason for why only powers of 5 can work! (to see why they all work, see Mark Hennings link):

Notes: Here F(n) denotes the nth term of the Fibonaccy sequence. The = sign usualy denotes congruence.

Lemma 1: If n does not work, then nk also doesn't for any natural number k. This is quite obvious, I think everyone can figure out a proof of this. What this lemma suggests is that we will try to find prime nubers that work and then try to convinate them and see if that works (as extra that we won't need to use you can try to proof that if there exists coprime p and q that both work then pq also works).

Lemma 2: If the F(m)=0 then the F(km)=0 (mod n) for any natural number k. This is also quite simple, if the F(m-1)=a=F(m+1) then it can be proven by induction that the F(m+i)=a F(i) thus F(m+m)=F(2m)=a F(m)=a*0=0 and again by induction F(3m)=0... F(km)=0.

What this lemma says is that if m is the smallest natural number such that F(m)=0, then the frequency of 0 is 1/m so that if we want n to work we must have 1/m=1/n so that m=n and F(n)=0 (mod n). So lets look for primes p that satisfy p|F(p)

To do this we must know or deduce from its closed form, an expression for the Fibonaccy sequence in terms of a sumation of binomial coefficients and powers of 5. Then since p dis prime it divides all the binomial coeficients C(p,2k+1) exept when k=(p-1)/2 (p is odd). This leaves p|5^((p-1)/2) (belive me if you don't have the formula in your mind) wich obviously has the only solution p=5.

Finally for Lemma 1 the only possible n to work are the powers of 5. It is analitically much more difficult to see why they all work but now that you know that they are the only possible ones you can try some (with a computer program) to be sure that at least the sum of its reciprocals aproches 1/(1-1/5)=5/4=1,25.

Incomprehensible problem, and each unrelated 'solution' or comment is a total mystery as well. How erudite, how refined, oh my, how sophisticated!

Jesus, I PAY for this! Ridiculous!

Bill Weihmiller - 2 years, 7 months ago

You pay for access to courses. The weekly questions are free.

Alperen AYDIN - 2 years, 7 months ago

양 우진
Sep 24, 2018

This is not an accurate answer but an approximation . You can change the value of "big_number" to whatever value you want.

U R brillird

왕자 어린 - 2 years, 8 months ago

But the sum of the numbers in the period over the lenght of the period (of the Fibonaccy sequence mod(n)) being (n-1)/2 I agree is necessary condition, but why is it sufficient?

Pau Cantos - 2 years, 8 months ago

Well you're correct. There should be a condition that all numbers(from 0 to n-1) should be in there in same times. When I wrote the program first, I just assumed that all numbers do exist in rest sequence. I'm modified the program and thank you for your advice :)

양 우진 - 2 years, 8 months ago

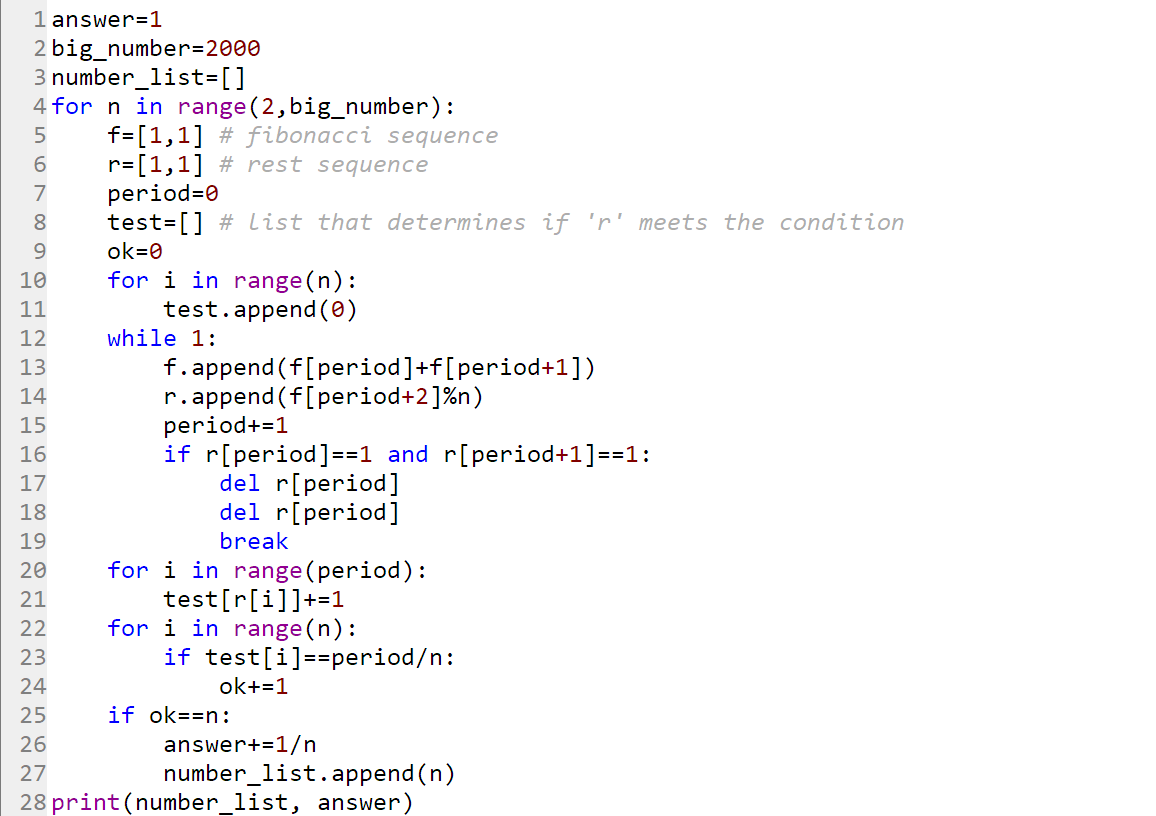
This is my Python solution. It gets slow for n>1000, but by then I could check the pattern on specific larger n.

for n in range(1,1000):
    L = [1,1]    # remainder sequence
    while True:
        if L[-2:] == [1,0]:
            break
        L.append((L[-2] + L[-1]) % n)
    R = [L.count(i) for i in range(n)]    # counts number of each value in L
    if len(set(R)) == 1:    # checks if R has one unique value
        print(n)

Malte Juhl - 2 years, 8 months ago

Vinod Kumar
Sep 25, 2018

Solution is sum of series [1/5^k, from k=0 to infinity]=(5/4). Sequence F(n) mod (5^k) has equal distribution of reminders.

Answer=1.25

Fibonacci Remainder!

The answer is 1.25.

4 solutions

0 pending reports