Field from Half Wire
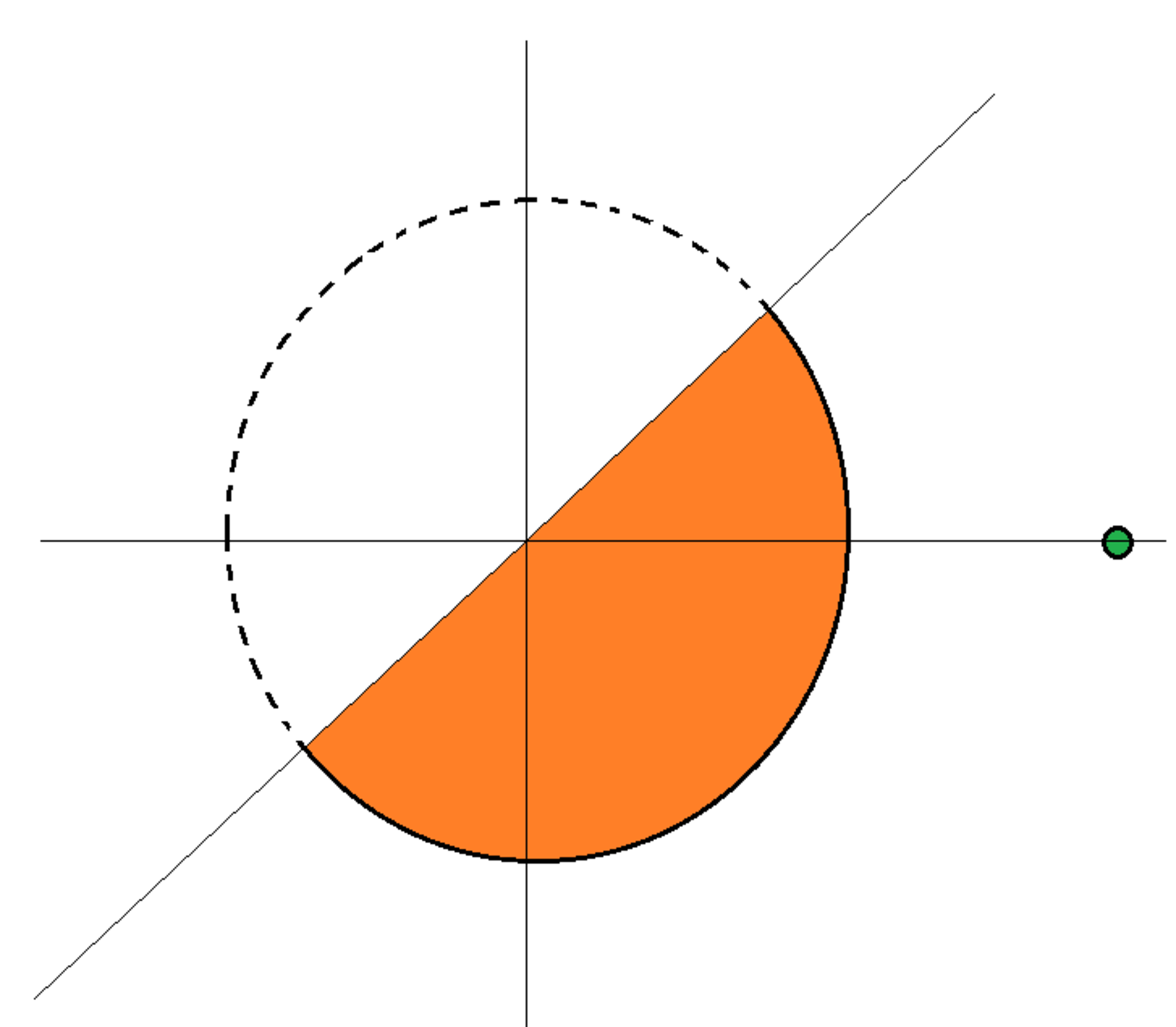
A solid circular half wire has the following shape:
x 2 + y 2 ≤ 1 y ≤ x − ∞ ≤ z ≤ ∞
The wire carries a current in the z direction, and there is one unit of current per unit of cross-sectional area of the wire. What is the absolute value of the magnetic flux density B at point ( x , y , z ) = ( 2 , 0 , 0 ) ?
Details and Assumptions:
1)
Magnetic permeability
μ
0
=
1
The answer is 0.1456.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
General guideline for solution. The tedious computations can be outsourced to Wolfram-Alpha. Consider a general point within the orange region ( x , y ) . Position vector joining ( 2 , 0 ) and that general point directed towards ( 2 , 0 ) is:
R = ( 2 − x ) i ^ − y j ^ R ^ = ∣ R ∣ R
The magnetic field due to an infinite current-carrying wire where current flows along the Z direction is:
B = 2 π ∣ R ∣ μ o I ( k ^ × R ^ )
Applying this formula to an area element in the given region yields:
d B = 2 π ( 2 − x ) 2 + y 2 d y d x ( ( 2 − x ) 2 + y 2 ( 2 − x ) i ^ − y j ^ )
d B x = 2 π 1 ( ( 2 − x ) 2 + y 2 ) y d y d x = f 1 ( x , y ) d y d x d B y = 2 π 1 ( ( 2 − x ) 2 + y 2 ) ( 2 − x ) d y d x = f 2 ( x , y ) d y d x
B x = ∫ − 1 / 2 1 / 2 ∫ − 1 − x 2 x f 1 ( x , y ) d y d x + ∫ 1 / 2 1 ∫ − 1 − x 2 1 − x 2 f 1 ( x , y ) d y d x B y = ∫ − 1 / 2 1 / 2 ∫ − 1 − x 2 x f 2 ( x , y ) d y d x + ∫ 1 / 2 1 ∫ − 1 − x 2 1 − x 2 f 2 ( x , y ) d y d x
@Karan Chatrath I have solved using symmetry.
@Karan Chatrath Sir please can you please help me in this problem . The question is related to complex numbers .
If
m
is the minimum value of
∣
z
∣
+
∣
2
z
−
w
∣
and
∣
w
∣
=
1
.
Then find the value of
4
m
?
Log in to reply
I think that the answer is 2. But when you ask help for problems, I suggest that in future you show your attempt.
Log in to reply
@Karan Chatrath Ok sir. From next time i wll definitely show my attempt. BTW please can you give me the solution of this problem?
Log in to reply
@A Former Brilliant Member – @Karan Chatrath sir can you please send your solution?
Log in to reply
@A Former Brilliant Member – Take w = ( 1 , 0 ) and z = ( x , y ) . The function to be minimised is:
f = x 2 + y 2 + ( 2 x − 1 ) 2 + 4 y 2
Solve:
∂ x ∂ f = 0 ∂ y ∂ f = 0
You will get: x = 0 . 5 and y = 0 . Perform a second derivative test to confirm that the point corresponds to a minima.
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
Sir while solving this equations in wolfram, the graph is correct but it is saying no solution. Below I have attached a screenshot
Log in to reply
@A Former Brilliant Member – Solve it by hand. See the second equation. It is zero when y = 0 . Use y = 0 in the first equation and solve for x .
Log in to reply
@Karan Chatrath
–
@Karan Chatrath
sir i performed second derivative test, results are attached, now how I should solve this 2 equations?


Log in to reply
@A Former Brilliant Member – What are you trying to accomplish? I do not understand why you have done as shown. PLease explain.
Log in to reply
@Karan Chatrath – @Karan Chatrath sir aapne kaha tha ki mai 2nd derivative test karu ye jaane ke liye ki point (0.5, 0) minima hai, ab maine 2nd derivative kiya, ab mai kya karu?
Log in to reply
@A Former Brilliant Member – This is not how the second derivative test is done for functions of multiple variables. Search on the internet about how it is done. Also, even in the one variable case (simple maxima-minima), one never computes the second derivative, equates it to zero and solves the resulting equation.
F u n p r o b l e m
Due to symmetry this problem can be converted into this A ( 2 , − 2 )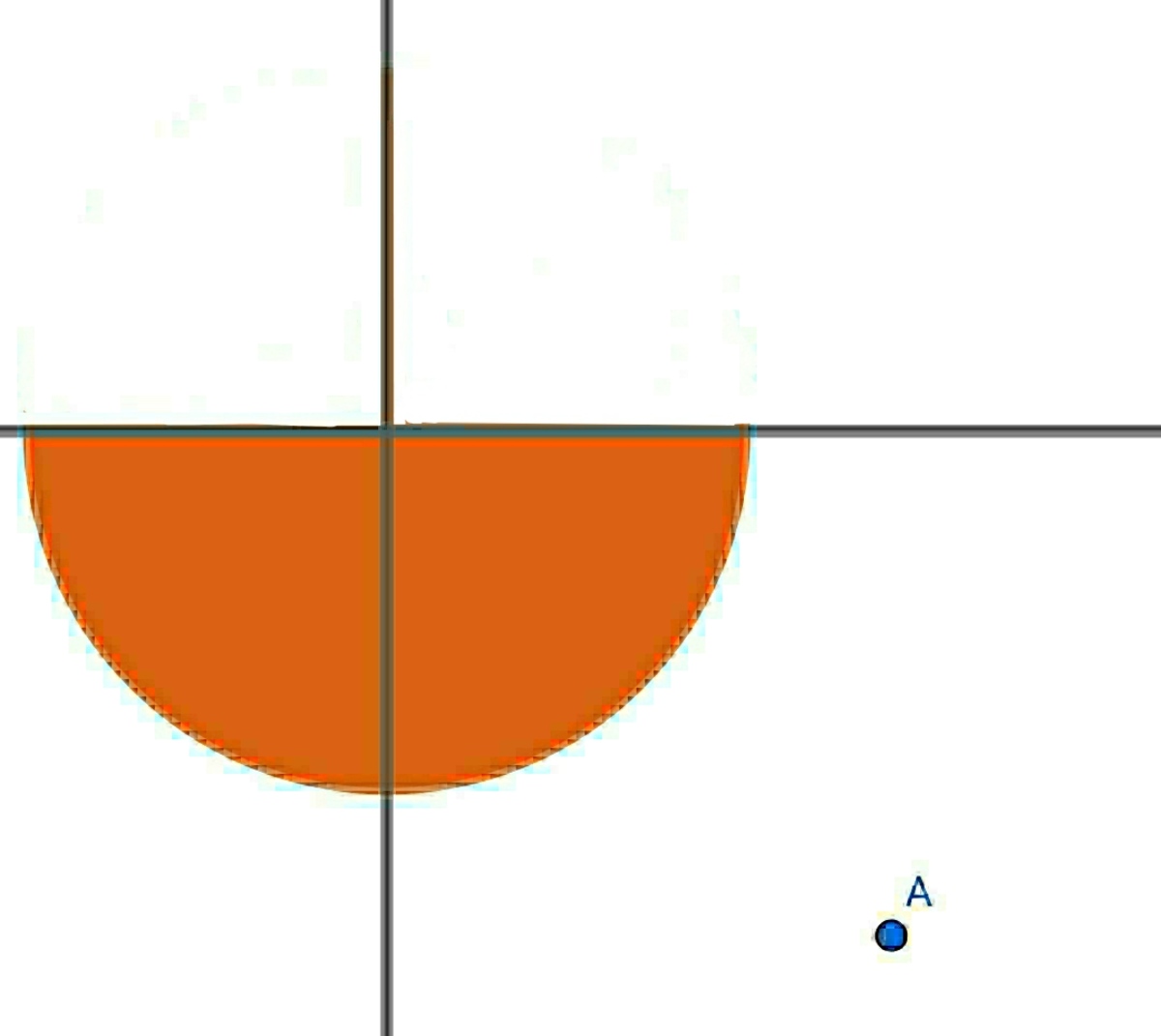
I will not show all the basic steps untill anybody asks me. @Karan Chatrath has also explained basic steps for this types of problem earlier.
Finally I reach
B x = ∫ − 1 + 1 ∫ − 1 − x 2 0 ( 2 π ( ( x − 2 ) 2 + ( y + 2 ) 2 ) ) 2 + y d y d x ≈ 0 . 0 8 9 6 9 5 4 B y = ∫ − 1 + 1 ∫ − 1 − x 2 0 ( 2 π ( ( x − 2 ) 2 + ( y + 2 ) 2 ) ) 2 − x d y d x ≈ 0 . 1 1 4 7 7 5
B n e t = B x 2 + B y 2 ≈ 0 . 1 4 5