Field Line Plot
There are two uniform spherical charge distributions, each with radius 1 . Distribution 1 is centered at ( x 1 , y 1 , z 1 ) = ( − 2 , 0 , 0 ) and has charge + 1 . Distribution 2 is centered at ( x 2 , y 2 , z 2 ) = ( 2 , 0 , 0 ) and has charge − 1 . Let us plot the electric field lines in the following manner.
1)
Begin at point
(
x
0
,
y
0
,
z
0
)
=
(
x
1
+
cos
θ
0
,
y
1
+
sin
θ
0
,
0
)
2)
Update the coordinates as follows:
x k = x k − 1 + ϵ E ^ x k − 1 y k = y k − 1 + ϵ E ^ y k − 1 z k = 0
3)
Continue plotting until the field line hits the boundary of charge distribution
2
4)
Make plots for the following values of
θ
0
, resulting in
2
5
field lines:
±
1
2
0
∘
,
±
1
1
0
∘
,
±
1
0
0
∘
,
±
9
0
∘
,
±
8
0
∘
,
±
7
0
∘
,
±
6
0
∘
,
±
5
0
∘
,
±
4
0
∘
,
±
3
0
∘
,
±
2
0
∘
,
±
1
0
∘
,
0
∘
In step 2 , subscript k denotes the present value, and subscript ( k − 1 ) denotes the previous value. E ^ is a unit-length version of the net electric field at point ( x , y , z ) . The parameter ϵ is a very small number.
What is the combined length of all 2 5 field lines?
Details and Assumptions:
1)
4
π
ϵ
0
1
=
1
2)
To check results, it helps to run the plotter with
ϵ
values spanning several orders of magnitude.
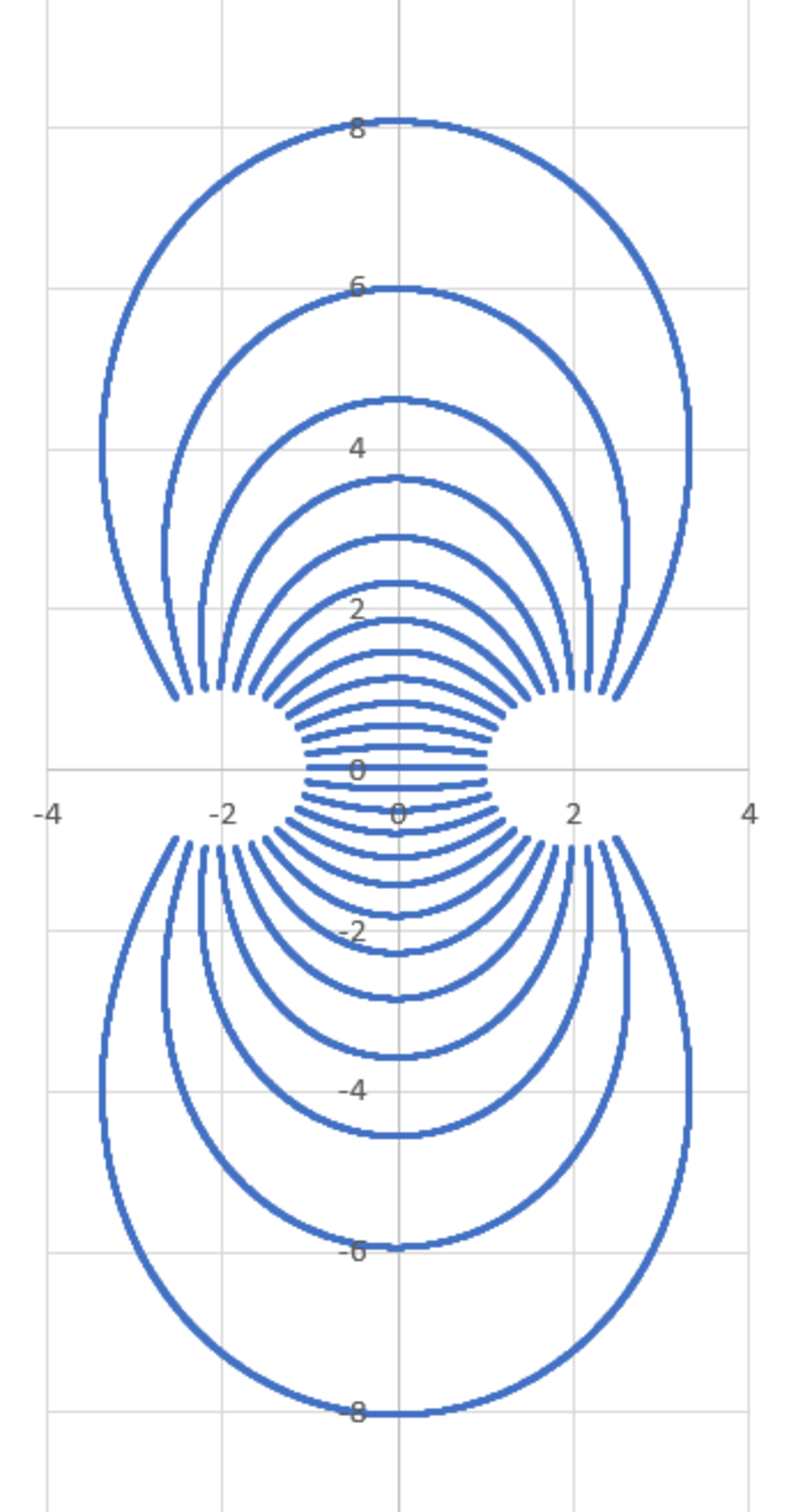
The answer is 150.6.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Thanks for the solution. I would also like to make the plots for both distributions having positive charge, but the "while" loop conditions might be a bit trickier to establish.
Log in to reply
You could create a boundary which is a larger circle (containing the charge distributions) centred at the origin. So that's where the lines could be plotted till.
Log in to reply
@Karan Chatrath Sir I always like Your solution . Can you please post solution Of this question https://brilliant.org/problems/hemisphere-e-field-quantitative/. In your style . First taking position vector . Actually I am not able to take elemental area and all those things can you help me?
Log in to reply
@A Former Brilliant Member – I will post when I can. In the meantime, ask google about 'the derivation of a surface area element in spherical coordinates'. You should find some helpful material. Also, recall that an area vector is always normal to a surface.
Nice problem as always. This time, I am only pasting the script of code I wrote to solve this. I hope it is readable. I will make amends to better it, if necessary.