Fill It Up With Pawns
What is the maximum number of pawns that can be placed on an 8 × 8 chessboard such that each row, each column, and each long diagonal contains at most 4 pawns?
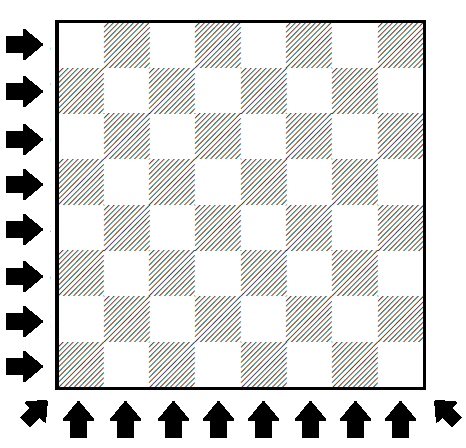
The answer is 32.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
6 solutions
Moderator note:
For completeness, apart from showing that 32 can be achieved, you should explain why 32 is an upper bound. This way, we have established that it is indeed the maximum
What about the already placed pawns
Log in to reply
The problem seems to make no reference to the image
Log in to reply
Then why that image is given? I thought according to that image we need to solve
Log in to reply
@Hardik Jain – I don't know, anyway in that case one solution can be like this https://drive.google.com/file/d/0B_1ESs6FObI7MjVOLXVpdWZ6Wk0/view?usp=sharing
Log in to reply
@Matteo Monzali – Then too answer is 28 as 4 centre pawns were already kept then we have to place the pawns
Log in to reply
@Hardik Jain – Assuming that the 4 center pawns have to be placed, can you prove that we can have a maximum of 28 pawns? If so, you should post that version of the problem.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator who can fix the issues.
@Hardik Jain – Unless we must count them, you should ask to Lee Care Gene who has created the problem
Log in to reply
@Matteo Monzali – How to contact him?
Log in to reply
@Hardik Jain – I think you can write @name to contact him here, for example @hardik jain (i don't know if it works but i've seen it in other discussion!) :)
I think the answer should be zero becoz its given at most 4 pawns which means i can put no pawns anywhere
Log in to reply
It asks for the "maximum number of pawns".
You have found the minimum number.
Log in to reply
Yes....yesss......u r right sir ....... I never read the question properly
Apart from just understanding the reason for why 32 pawns is an upper bond for really being complete it also quite necessary to understand how to obtain the configurations that work.
You can just show (and pretty much just show) a configuration and then you proved that it works therefore the proof being indeed complete as long as the bond is established but by this the understanding wouldn't because the step which will necessary still be done , that of achieving the configuration would remain not articulate in that understanding and could also be just a luck anyway.
I'll just talk a little about how such constructions can be obtained and their reasoning. And , anyway am hoping I will be clear regarding that reasoning.
If therefore , it is asked how to obtain all those constructions that work this implies obtaining an understanding of when for a given configuration of pawns all the rows , columns and long diagonals have at most 4 pawns where this rows , columns and long diagonals can't be initially covered under one synthetic expression and therefore makes impossible to verify when for a configuration checking the restrictions in one of the 3 the restrictions are also checked in the others because they are thought separately more clearly meaning that thinking of one I don't take into consideration the other. As this is the case what must be done is to obtain such a synthetic expression precisely because it's lack is responsible for not representing all of them together (that meaning that when I think of them by this synthetic expression I can cover and verify all without having problems as at first) which can be done maybe in a number of different ways and I say maybe just because I'm not completely sure that it can be done in more than one way being anyway pretty complicated to be sure of meta-logical considerations too often. To obtain such a synthetic expression one way of doing it is by thinking in the terms of how to put all the 32 pawns in one of either all the rows or all the columns while at the same time thinking when I place the pawns in , say , all the rows how does this way of placing affects the restrictions at the same in the columns and the long diagonals.
More clearly , firstly just convert this problem into the terms of placing the pawns in all the rows however this happening by not forgetting when placing them about the columns and diagonals. By considering things like this it is obtained that synthetic expression pretty direct. Therefore considering this idea by placing 4 pawns in each of the 8 rows thinking also at the restrictions that have to be respected for the columns and long diagonals observe firstly that for any row placing 4 pawns affects 4 different columns. Because of that it means that in order for all columns to have a number of 4 pawns any place from the configuration of pawns of a row should be for that row common with 3 other rows this checking the first restriction for the columns which however is not as restrictive as the the other one. After restriction 1 regarding the columns is understood consider the restriction 2 regarding the 2 long diagonals. In order to not exceed the limit of 4 pawns on the long diagonals some places on configuring the pawns on rows should be avoided. This places are anyway of course at the intersection of the rows and long diagonals and observe that it is possible to anyway put all the pawns on rows such that none stands on this 4 squares and still respect the restriction regarding the columns so with diagonals it is no problem. Just by such consideration the problem anyway can be solved easily and obtained an understanding of the construction.
Anyway , an interesting thing to note is that you can consider a general rule of distribution therefore a regularity among the rows such that you obtain solutions regarding the distribution on columns. Anyway also the solution provided up is exactly one such example of regular distribution of pawns and a good example of this.
We know it from the Dirichlet's rule (every pawn has its row and there are 8 rows, so if there were more than 32 pawns, one pawn would contain more than 4 pawns)
for maximum columns-row

adjust it to satisfy the long diagonal condition

Exactly how I thought it lol.
Row wise-start from first row placing 4 pawns from left to 4 places right. Then by leaving one row place it in the next.Continue this till the last row. Therefore 8×4=32 is the minimum no of pawns required to satisfy the given condition.
You mean the maximum, right?
Dogs are pawn and cats are not available cases.
 This one is as true as much as it's cute.
This one is as true as much as it's cute.
place 4 pawns on a row, then place four pawns on the spot you didn't place it on the next row. Repeat it four times, then you only have four pawns every column. 4 x 2 x 4=32
Two solutions are to put the pawns either on all the black or all the white squares. This fully maximizes the number of pawns since a pawn placed anywhere else would add a fifth pawn to one row and one column.
I found one solution that is like this