Filling in a 3x3

Insert the numbers into the diagram one at a time, in order from 1 to 9. Each number has to be placed in an upper-left corner (there may be more than one way to do this). Forgetting about which number is in which box, just look at the shape they make. The number of ways to arrange numbers for each shape is always equal to the sum of the shapes feeding into it. The solution (42) is at the bottom.

By the hook length formula , the number of possible grids is $\frac{9!}{5 \cdot 4 \cdot 3 \cdot 4 \cdot 3 \cdot 2 \cdot 3 \cdot 2 \cdot 1} = 42.$

Notice that grid must be of the form:

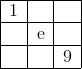
where $4\leq e\leq 6$ . This splits up into two forms:

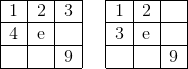
where $5\leq e\leq 6$ for the first one, while still $4\leq e\leq 6$ for the second one. Regarding 1st one, for $e = 5$ there are 3 ways to fill the grid, namely:

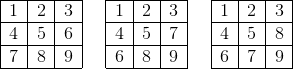
For $e = 6$ there are two ways:

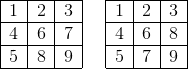
Regarding 2nd form, for $e = 4,5$ there are 6 ways to fill the grid:

For $e = 6$ there are 4 ways:

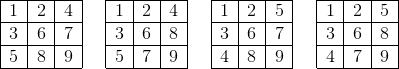
Notice that each of our solutions can be flipped over the main diagonal $(1-e-9)$ . Hence, the total number of ways is $2\times (3 + 2 + 6 + 6 + 4) = 42$ .

This is the standard Young Tableaux and answer for n=3 is 42.

I just guessed 42.

(1,1) entry must be 1. (3,3) entry must be 9. Every valid shape can be transposed so we can count only shapes that (1,2) entry is 2. Assume first row is 1,2,3. We should consider how many valid ways there are for the second row. The third row is by definition the remaining numbers in increasing order. So we have (4,5,6), (4,5,7), (4,5,8), (4,6,7), (4,6,8). 5 options. If we look on 1,2,4 as the first row and replace 4 with 3 in the second row we will get another 5 options. 1,2,5 gives another 5. (3,4,6), (3,4,7), (3,4,8), (3,6,7), (3,6,8). 1,2,6 gives another 4 (3,4,7), (3,4,8), (3,5,7) and (3,5,8). And finally 1,2,7 gives another 2 (3,4,8) and (3,5,8). Total of 21. Transpose of these options gives another 21 and in total 42.