Find lo g 1 0 n m
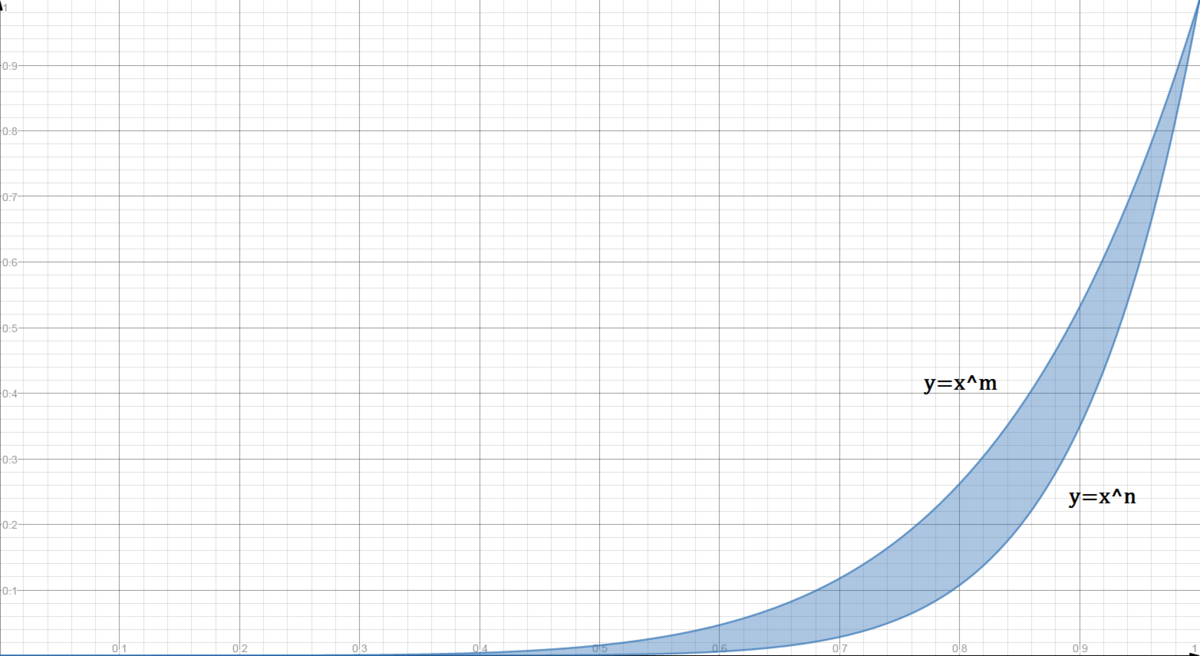
Let m and n be two distinct positive integers such that m < n < m 2 .
If the area of the region bounded between y = x m , y = x n , x = 0 and x = 1 is equal to 7 7 4 , then which of the following is the value of lo g 1 0 n m .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution

Nice question. I find that ( m , n ) = ( 1 8 , 1 4 6 2 ) also works, which gives lo g 1 0 n m ≈ 5 6 . 9 7 , which of course isn't one of the given options, so of the given options 6 is the unique answer.
Log in to reply
Thanks for the Information ,I did not knew such a possibility existed .
Your solution is incomplete. You still haven't proved that 7, 10, 11 are not a possible value of lo g 1 0 n m .
Log in to reply
Let a = m + 1 and b = n + 1 . Then we have that
a 1 − b 1 = 7 7 4 ⟹ 7 7 b − 7 7 a = 4 a b ⟹
4 a b + 7 7 a − 7 7 b = ( 2 a − 2 7 7 ) ( 2 b + 2 7 7 ) + ( 2 7 7 ) 2 = 0 ⟹
( 7 7 − 4 a ) ( 4 b + 7 7 ) = 7 7 2 = 7 2 × 1 1 2 .
Then since a , b > 0 we need to distribute the factors of 7 7 2 to 7 7 − 4 a and 4 b + 7 7 in such a way that we get positive integer solutions for a , b . For example,
7 7 − 4 a = 7 2 , 4 b + 7 7 = 1 1 2 ⟹ ( a , b ) = ( 7 , 1 1 ) , ( m , n ) = ( 6 , 1 0 ) ,
7 7 − 4 a = 1 , 4 b + 7 7 = 7 7 2 ⟹ ( a , b ) = ( 1 9 , 1 4 6 3 ) , ( m , n ) = ( 1 8 , 1 4 6 2 ) .
These turn out to be the only factor-splitting options that yield integer results, thus ruling out 7 , 1 0 , 1 1 as solutions to this problem.
I think this problem is overrated.
Log in to reply
You are also.
Log in to reply
Ya very true. I am quite overrated. I think i shall have been to calculus lvl 3 and others also. :)