Find maximum area of rectangle
A rectangle's bottom is at y = 0
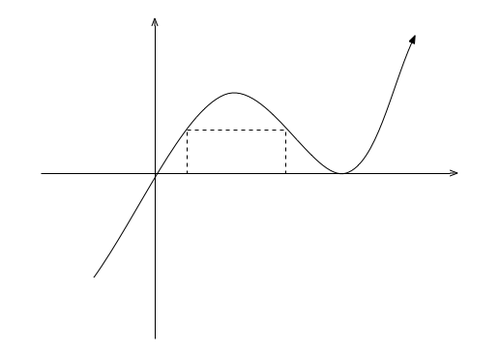
while its top corners are on the curve y = x ( x − 1 ) 2 between x = 0 and x = 1 . The maximum area of this rectangle can be expressed as
c d a a − b
where a and d are prime numbers. What is the sum a + b + c + d ?
(Don't count a twice)
The answer is 128.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I say your area function is easier to maximize. Very nice.
Hi Jatin, nice solution. I did it using Lagrange Multipliers (I don't know the theory behind it but just know a little bit about the application; I guess we shall be learning it soon) ⌣ ¨ .
@jatin yadav well how did you maximize your area function? I got a 5-degree equation while trying to do so....could you please help because that's the main part of the solution......
Log in to reply
Set d α d A = 0 , solve for α and take α > 1 .
Log in to reply
Thanks but I did not mean that. I'm saying that it's very hard to find the solution when you differentiate it.... I got a five degree equation..... of which even Wolphram Alpha gave approximate answers..
Log in to reply
@Led Tasso – Why didn't you make any simplification? I ended with a quadratic equation: 6 α 2 − 1 0 α + 3 = 0 .
@jatin yadav I got the same area function as you and found α = 6 5 + 7 . From there, how did you simplify it?
Doing this in a straightforward way, let x = p be the left side of the rectangle. Then the other point is a root of the equation
x ( x − 1 ) 2 − p ( p − 1 ) 2 = 0
But ( x − p ) is already one of the factors, so dividing this factor out, we have the quadratic to solve
x 2 + ( p − 2 ) x + ( p − 1 ) 2 = 0
which the smaller of the roots > p is
x = 2 1 ( 2 − p − 4 p − 3 p 2 )
We then have the area of the rectangle to maximize
( 2 1 ( 2 − p − 4 p − 3 p 2 ) − p ) p ( p − 1 ) 2
A bit of tedious calculus gets us the maximum
1 0 8 3 7 7 − 1 0
so that a + b + c + d = 1 2 8
Question, if you didn't limit the rectangle between x=0 and x=1, keeping its base on y=0, would the greatest possible rectangle have one of its points on the max value of the curve between x=1, and x=0.
Log in to reply
Well, yes, then it would be a different problem to solve. Then we'd be using the other root that's further away from p.
Edit: That's interesting, it turns out that the maximum area of such a rectangle is
1 0 8 3 7 7 + 1 0
so that the answer is still 1 2 8 . How about that.
Sir could u pls tell me how did u maximize the area?'
nice, but i wanted to avoid the tedious calculations :(
A horizontal line satisfing 0 < y < 2 7 4 meets the graph in 3 points, x = α , β , , and γ .
Say α is the largest, hence α > 1 . Thus x = β , and x = γ constitute the vertical sides of rectangle.
Now, x ( x − 1 ) 2 = α ( α − 1 ) 2
Using vieta's formulae,
α + β + γ = 2 ,
α β + α γ + γ β = 1
Multiplying first equation by α and subtracting second , we get:
β γ = α 2 − 2 α + 1
Also, β + γ = 2 − α
Hence, ∣ β − γ ∣ = ( β + γ ) 2 − 4 β γ = 4 α − 3 α 2 .
Hence, the sides of rectangle are α ( α − 1 ) 2 , and 4 α − 3 α 2
Thus , area is A ( α ) = α ( α − 1 ) 2 4 α − 3 α 2
Maximise it to get A m a x = 1 0 8 3 7 7 − 1 0