Find Maximum Volume Of Ruled Frustum
The solid figure shown has a height of 2, with a square top of area 2 and a circle base of area π , the centers of which lie on the same axis that both faces are perpendicular to.
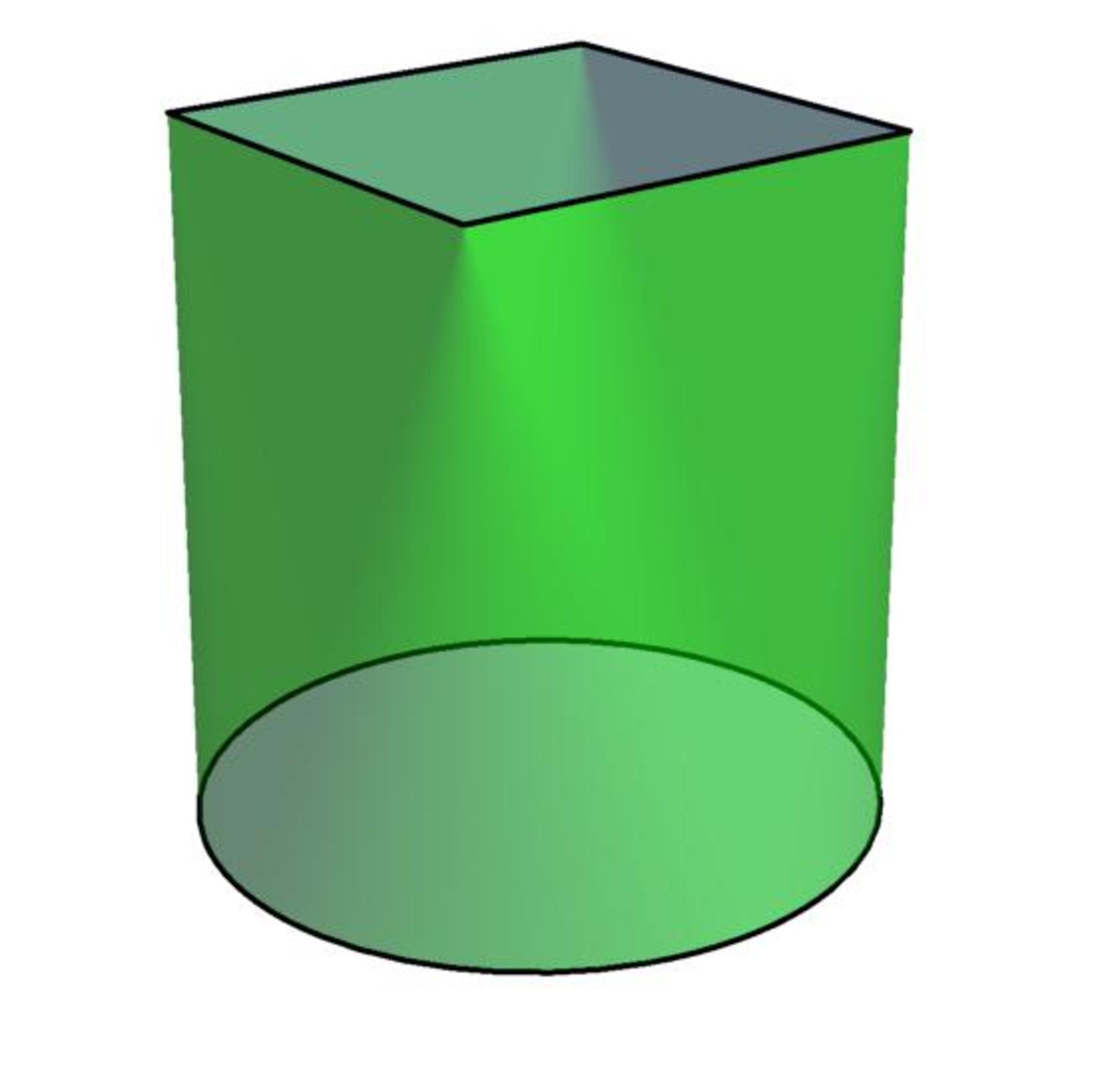
The surface that extends from the top face to bottom face is a ruled surface , which is a surface where any point on it lies on a line of points also on the same surface extending from the edge of the top face to the edge of the bottom face. No point on the surface lies on more than one such line.
The maximum volume of this solid can be expressed as
a 1 ( b + c d + e π ) ,
where a , b , c , d and e are all positive integers, d is square-free, and a and b are coprime. Find the sum a + b + c + d + e .
Details and Assumptions :
-
There can be more than 1 kind of ruled surface that spans from the top to bottom face.
-
A finite few points may lie more than one line on the ruled surface, and by "maximum", it may or may not only be a supremum .
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
I don't think I've ever seen Calculus of Variations used to solve a problem posted either in Brilliant, or in Yahoo!Answers, where I used to be before I came here. This is an impressive display of how to actually put it to practical use. Because of those corners, I don't think I would've known where to even start.
It's also a great example of how to tackle this problem by first looking at this as a supremum instead of a maximum, as a way of getting around that "corners" problem. I now understand why the careful language you had suggested that I put in the Details part of the problem. Very interesting! Also, many thanks for conferring credibility to my problem! I know that my own solution is kind of on the sketchy side, but, hey, it worked, didn't it?
Log in to reply
Thanks for the comments. As it happened, I did not really have to use CoV at all. Since the final integral does not depend on θ ′ ( t ) , the Euler equation is trivial, showing that an extremum does not exist. Finding the supremum was a simpler task. It took me a while to make my argument sufficiently general. I had originally assumed that the rules from the four vertices of the square were parallel to the axis of the system (cheating by looking at your diagram). It was a bit more effort to show that this assumption was not necessary
You might like this one , then.
The maximum volume is 3 1 ( 4 + 4 2 + 2 π ) , so that the answer is 1 5
To get a good start on this, go look up Zheng's The Prismoidal Formula
Let the area of the parallel cross sections of a solid be a 3 rd order polynomial function of z , where z is the height parameter perpendicular to the cross sections, the polynomial being of the form
A ( h ) = a 3 z 3 + a 2 z 2 + a 1 z 1 + a 0
where the coefficients are arbitrary reals
Then the definite volume integral is, for z = 0 to z = h
V = 4 1 a 3 h 4 + 3 1 a 2 h 3 + 2 1 a 1 h 2 + a 0 h
For z = 0 , z = 2 1 h , and z = h , the cross section areas are
A
(
0
)
=
a
0
A
(
2
1
h
)
=
8
1
a
3
h
3
+
4
1
a
2
h
2
+
2
1
a
1
h
1
+
a
0
A
(
h
)
=
a
3
h
3
+
a
2
h
2
+
a
1
h
1
+
a
0
so that the following formula will yield the same volume as per the definite volume integral
V = 6 1 h ( A ( 0 ) + 4 A ( 2 1 h ) + A ( h ) )
This is the versatile Prismoidal Formula. Let the perimeters of the top and bottom faces be defined by polygons which successive vertices have coordinates
( x 1 , y 1 ) , ( x 2 , y 2 ) , ( x 3 , y 3 ) . . .
and
( X 1 , Y 1 ) , ( X 2 , Y 2 ) , ( X 3 , Y 3 ) . . .
so that the points on the ruled surface can be defined parametrically by z
( x 1 z + X 1 ( h − z ) , y 1 z + Y 1 ( h − z ) ) , ( x 2 z + X 2 ( h − z ) , y 2 z + Y 2 ( h − z ) ) , . . .
Using the Shoelace Formula , the area of any cross section A ( z ) works out to be a 2 nd order polynomial of z , which means that the volume of any such frustum with a ruled exterior surface can be determined solely by the areas of the top face, mid-cross section, and bottom face. Hence, for the maximum volume, we seek the maximum possible area of the cross section at height 1 . The perimeter yielding such maximum area is shown in red in this figure
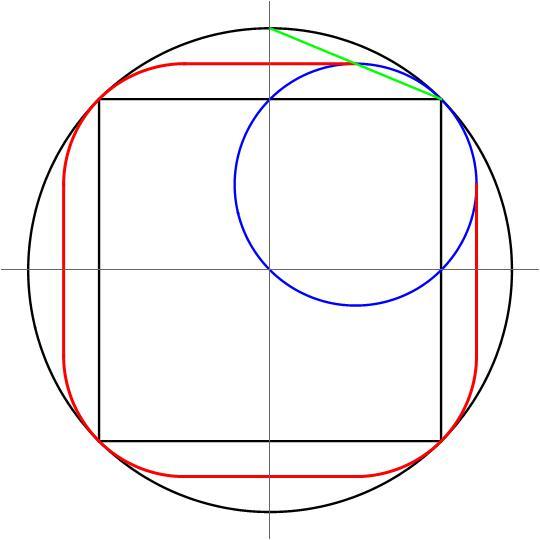
One of the lines of the ruled surface is shown in green, where the red perimeter bisects it. The locus of the midpoint of a green line that has one end pivoting about a fixed point while the other end moves along a straight line is a straight line of half of the length. The locus of the midpoint of a green line that has one one pivoting about a fixed point while the other end moves along a circle is a circle of half the radius. The area of this cross section defined by the red perimeter is readily found to be
A ( 1 ) = 2 1 + 2 + 4 π
This, together with the area of the square top which is 2 , the area of the circle base which is π , and a height of 2, and using the Prismoidal Formula, yields the volume
V = 3 1 ( 4 + 4 2 + 2 π )
Note: Use of polygons and the Shoelace Formula for finding the areas of them can be generalized to the continuous case, as for the example the circle or parts of it here.
What an awesome problem, with a very neat solution! +1
Log in to reply
I still haven't figured out your coin problem.
Log in to reply
I used graph theory. Have you considered using a colouring?
Log in to reply
@Sharky Kesa – No, but that's a good idea. I'll go sleep on it now.
Log in to reply
@Michael Mendrin – Did you get it in the end?
Log in to reply
@Sharky Kesa – No, it's in that stack of unfinished projects on my desk, so to speak. Man, things can just pile up like that.
@Michael Mendrin - Nice solution!! One question: How do you know that the red cross-section is the one with the maximum area? I see why it is one possible cross-section of the ruled surface. Why is it the one with maximal area? Thank you so much!!
Set up axes so that the origin is at the centre of the square end, and the circular end is in the z = 2 plane.
In a ruled surface for which no point lies on more than one rule, every point F ( t ) on the bottom square must be joined by a rule to a unique point on the top circle. This point will have coordinates G ( t ) = ( cos θ ( t ) , sin θ ( t ) , 2 ) 0 ≤ t ≤ 4 where, if the surface is to satisfy the "no point lies on two rules" condition, then θ ( t ) must be a strictly increasing function of t such that θ ( 4 ) = θ ( 0 ) + 2 π . We shall assume that θ ( t ) is continuously differentiable, so that we can perform the necessary integrals.
The cross-section of the surface at height z is defined by the function ( X z ( t ) , Y z ( t ) , z ) = 2 2 − z F ( t ) + 2 z G ( t ) for 0 ≤ t ≤ 4 . The area of this cross-section is given by Stokes' Theorem as A ( z ) = = = 2 1 ∫ 0 4 [ X z ( t ) Y ˙ z ( t ) − Y z ( t ) X ˙ z ( t ) ] d t 2 1 ( 2 2 − z ) 2 ∫ 0 4 [ F 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) F ˙ 1 ( t ) ] d t + 2 1 ( 2 z ) 2 ∫ 0 4 [ G 1 ( t ) G ˙ 2 ( t ) − G 2 ( t ) G ˙ 1 ( t ) ] d t + 8 z ( 2 − z ) ∫ 0 4 { F 1 ( t ) G ˙ 2 ( t ) + G 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) G ˙ 1 ( t ) − G 2 ( t ) F ˙ 1 ( t ) } d t 4 1 ( 2 − z ) 2 × 2 + 4 1 z 2 × π + 8 z ( 2 − z ) ∫ 0 4 { F 1 ( t ) G ˙ 2 ( t ) + G 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) G ˙ 1 ( t ) − G 2 ( t ) F ˙ 1 ( t ) } d t using Stokes' Theorem twice more to evaluate the first two integrals, and so the volume of the surface is V = = ∫ 0 2 A ( z ) d z = 3 2 ( π + 2 ) + 6 1 ∫ 0 4 { F 1 ( t ) G ˙ 2 ( t ) + G 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) G ˙ 1 ( t ) − G 2 ( t ) F ˙ 1 ( t ) } d t 3 2 ( π + 2 ) + 6 1 [ I 0 + I 1 + I 2 + I 3 ] where I 0 , I 1 , I 2 , I 3 are the integrals of F 1 ( t ) G ˙ 2 ( t ) + G 1 ( t ) F ˙ 2 ( t ) − F 2 ( t ) G ˙ 1 ( t ) − G 2 ( t ) F ˙ 1 ( t ) over the intervals [ 0 , 1 ] , [ 1 , 2 ] , [ 2 , 3 ] and [ 3 , 4 ] respectively. We can show that I 0 = = ∫ 0 1 { d t d [ ( 1 − t ) sin θ ( t ) − t cos θ ( t ) ] + 2 sin θ ( t ) + 2 cos θ ( t ) } d t − cos θ ( 1 ) − sin θ ( 0 ) + 2 2 ∫ 0 1 cos ( θ ( t ) − 4 1 π ) d t and, similarly, I 1 I 2 I 3 = = = − sin θ ( 2 ) + cos θ ( 1 ) + 2 2 ∫ 1 2 cos ( θ ( t ) − 4 3 π ) d t cos θ ( 3 ) + sin θ ( 2 ) + 2 2 ∫ 2 3 cos ( θ ( t ) − 4 5 π ) d t sin θ ( 4 ) − cos θ ( 3 ) + 2 2 ∫ 0 1 cos ( θ ( t ) − 4 7 π ) d t and hence V = 3 2 ( π + 2 ) + 3 1 2 [ ∫ 0 1 cos ( θ ( t ) − 4 1 π ) d t + ∫ 1 2 cos ( θ ( t ) − 4 3 π ) d t + ∫ 2 3 cos ( θ ( t ) − 4 5 π ) d t + ∫ 3 4 cos ( θ ( t ) − 4 7 π ) d t ] From this it is clear that V < 3 2 ( π + 2 ) + 3 4 2 = 3 4 + 4 2 + 2 π and also that this upper bound cannot be achieved with a continuously differentiable function θ ( t ) , since we would require something like θ ( t ) = 4 1 π for 0 < t < 1 , θ ( t ) = 4 3 π for 1 < t < 2 , θ ( t ) = 4 5 π for 2 < t < 3 and θ ( t ) = 4 7 π for 3 < t < 4 . This would mean that θ was not continuous! However, we can get arbitrarily close to this upper bound, by choosing a function θ like:
(getting closer and closer to the upper bound the more steeply the "jumps" are made, and the flatter the "plateaus" become). Thus, if we insist on continuously differentiable θ , the the value of 3 4 + 4 2 + 2 π is a supremum, and not a maximum.
If we drop the requirement for a continuously differentiable θ , and also ease the requirement that no point lies on two rules, we can achieve this supremum (which turns into a maximum). For this we need θ ( t ) = ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 4 1 π 4 3 π 4 5 π 4 7 π 0 < t < 1 1 < t < 2 2 < t < 3 3 < t < 4 In this solution the point ( 2 1 , 2 1 , 2 ) is joined to all the points ( t , 1 − t , 0 ) for 0 ≤ t ≤ 1 , the point ( − 2 1 , 2 1 , 2 ) is joined to the points ( 1 − t , 2 − t , 0 ) for 1 ≤ t ≤ 2 , and so on round the square, while the points ( 1 , 0 , 0 ) , ( 0 , 1 , 0 ) , ( − 1 , 0 , 0 ) and ( 0 , − 1 , 0 ) are each joined to all the points in a suitable quarter of the circle. These eight points on the surface each belong to an infinite number of rules, but all other points on the surface belong to a single rule only. This is the surface in the diagram given in the problem.