Find the altitude!

Geometry Level 5

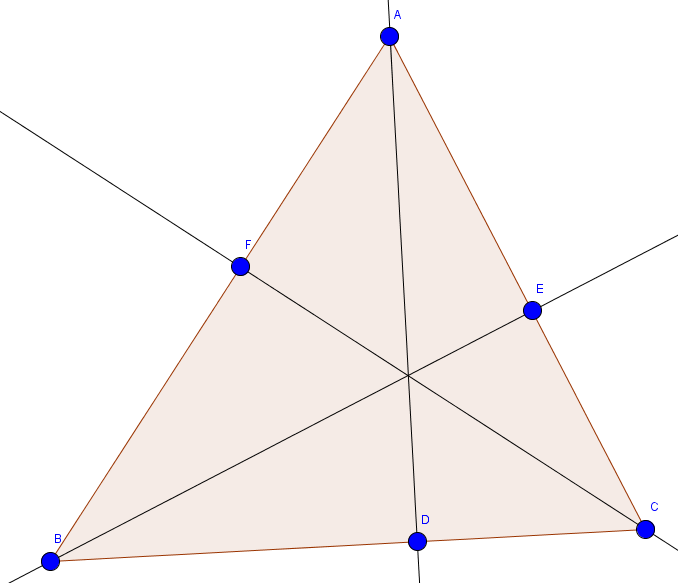$AD, BE, CF$ are the three altitudes of the triangle $ABC$ . If $AD=4$ and $BE=5$ , find the sum of all possible integer value of $CF$ .

The answer is 187.

2 solutions

Dexter Woo Teng Koon
Sep 20, 2016

$AB \times CF = 4BC = 5AC$

$AB + AC > BC$

$AB + \frac{AB \times CF}{5} > \frac{AB \times CF}{4}$

$20AB + 4(AB \times CF) > 5(AB \times CF)$

$20AB > AB \times CF$

$20 > CF$

$AC+ BC > AB$

$\frac{AB \times CF}{5} + \frac{AB \times CF}{4} > AB$

$4(AB \times CF) + 5(AB \times CF) > 20AB$

$9(AB \times CF) > 20AB$

$CF > \frac{20}{9}$

$\therefore$ The sum of all possible integer value of $CF$ is $\frac{3+19}{2} \times 17 = 187$

Did the same way!...+1

Ayush G Rai - 4 years, 8 months ago

Shouldn't you at least check that a triangle exists with, for example, $CF=3$ and $CF=19$ ?

Mark Hennings - 4 years, 8 months ago

Is there another way to check it? I thought that we proved that $\frac{20}{9} < CF < 20$ is enough

Dexter Woo Teng Koon - 4 years, 8 months ago

You have showed that the altitude $CF$ must lie between $20/9$ and $20$ . You have not showed that any value in this range can be the third altitude of a suitable triangle.

Since you can determine the three sides of a triangle from the values of the altitudes, however, this is not that difficult. Can you find the formula for the area of a triangle in terms of its three altitudes? From there, it is simple to get the three sides.

Mark Hennings - 4 years, 8 months ago

@Mark Hennings – Ok :) I'm trying to find it. I realized that I couldn't determine the value of three sides of the triangle from the value of the altitudes , i trying with finding the sides of the triangle with altitudes $4,5,6$ and end up with the ratio of the three sides will be in $15:12:10$ but it is not possible that the sides of the triangle are $15,12,10$

Dexter Woo Teng Koon - 4 years, 8 months ago

@Dexter Woo Teng Koon – If $A$ is the area of the triangle, then $h_a= \frac{2A}{a} \hspace{1cm} h_b = \frac{2A}{b} \hspace{1cm} h_c=\frac{2A}{c}$ Plug these into Heron's formula for the area, and you get $A=h^2\sqrt{\frac{h_a h_b h_c}{(h_a-2h)(h_b-2h)(h_c-2h)}}$ where $h^{-1}=h_a^{-1} + h_b^{-1} + h_c^{-1}$ The requirement that $h_a,h_b,h_c$ must all be bigger than $2h$ give the desired range for $h_c$ , given $h_a=4$ and $h_b=5$ .

Mark Hennings - 4 years, 8 months ago

@Mark Hennings – I would like to know how did you solve this problem :)

Dexter Woo Teng Koon - 4 years, 8 months ago

Niranjan Khanderia
Sep 26, 2016

Let CF=f.
From Triangular Inequality,
$If\ f\ is\ shortest, \ \ \dfrac {2*Area} f \ \ the\ longest \ side.\ \ \therefore\ \ \dfrac 1 4 +\dfrac 1 5\geq \ \dfrac 1 f.\\ \implies\ f \geq \dfrac{20} 9.\ \ \ For \ integer\ f, \ \ \ f >2.\\ If\ f\ is\ longestest, \ \ \dfrac {2*Area} f \ \ the\ shortest \ side.\ \ \therefore\ \ \dfrac 1 4 -\dfrac 1 f\leq \ \dfrac 1 5.\\ \implies\ f \leq \dfrac{20} 1.\ \ \ For \ integer\ f, \ \ \ f \leq 19.\\ \text{So f can take the value of all integers from 3 to 19}\\ \displaystyle \ Sum=\sum_{k=3}^{19} k=\dfrac {(19-3+1)*(19+3)} 2=\Large\ \ \color{#D61F06}{187}.$

Find the altitude!

The answer is 187.

2 solutions

0 pending reports