Find the area of the coloured region
Two congruent circles of radius 5 cm are drawn so that their centers are 1 cm apart.
What is the combined area of the two red-colored regions to the nearest square centimeter ?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
19 solutions
Jeremy -- I am having trouble visualizing the red region skewing that you describe. How would you arrange it/them and what part of it/them would you 'push' on to skew it/them ? I don't get it. :-)
Log in to reply
I edited my post to include a picture.
Log in to reply
Thanks much. It now looks like a mapping of a curved 'layer' into a 'straight' layer, maintaining the length & width. Is that a valid description that I gave ?
Log in to reply
@Jesse Otis – Right. Sort of like doing calculus without doing calculus.
Log in to reply
@Jeremy Galvagni – Okay, I now see how the 'skewing' takes place. My next question is how did you determine that the rectangle is 10 cm in 'length' and 1 cm in 'width' ?
Log in to reply
@Jesse Otis – 10 is the diameter of the circle. 1 is the offset.
Log in to reply
@Jeremy Galvagni – Sorry to keep bugging you about this - but I am confused. It seems to me that the rectangle would be longer than 10 cm because it is, before skewing, an arc forming the top half of the circle's circumference. Using S=R(theta), putting in numbers gives S=5(pi radians) = 5(pi) -- which, of course, is greater in value than 10 cm. If the two arcs were to be straightened out it would result in two line segments (which would be longer sides of the rectangle) that would make a rectangle 5pi cm. long. Or would it ? Thanks in advance for your patience and reply posts. JO
Log in to reply
@Jesse Otis – It's actually a bit less than 10cm. You can see the follow-up I posted for details.
You are measuring the arc length, which is not relevant. That would be like multiplying two side lengths to find the area of a parallelogram.
Log in to reply
@Jeremy Galvagni – Is what you are doing similar to, say, shining a light from 'under' the circles (the light is in the plane including the circles) onto a wall (perpendicular to the plane that includes the circles) above and the result is the top & bottom of the rectangle (from the 'upper' circle and the 'lower' circle respectively ?
Log in to reply
@Jesse Otis – Yeah, I guess so. I just think of it as a continuous skew.
Very clever!!
Jeremy -- Can you please tell how did you learn this technique? It can be quite useful for competitive exams. BTW, very clever solution.
Log in to reply
I have developed a good ability to visualize moving things around when I see a picture. I can't give a specific place. Just practice.
Beautiful! Imagination in maths can solve the most complex of problems !
Is this similar to Cavalieri's Principle in 2D?
Log in to reply
Yes, definitely.
yes ,you are right
i am Chinese,ni you so clever,butidont
wonderful!!
Don't know how to place my resolution :(
This method is supposed to give us the exact answer, but we know the answer isn't an integer. Why is the output an exact integer?
Log in to reply
It's not exact because the lower part of the circle centered at (0/1) will "curve inwards" a bit, making the exact area a bit smaller.
Log in to reply
I would only add that this integral is approximate, rather than exact, only because the limits of integration are not exact. Each would have a magnitude of a smidge less than 5, rather than exactly 5.
Isn't that a shape of an eclipse?? When you take the area of the eclipse and subtract from it the area of the circle you get a different answer!!!
Log in to reply
In fact, no. This new shape actually has corners on its sides.
Log in to reply
But the answer is way off of 20 cm. Those corners are barely visible.
Log in to reply
@Martin Karroum – I don't understand. The area is very close to 20 cm.
I also thought the answer would be found by subtracting an ellipse of r^2cm = 20 from an ellipse of r^2cm = 30. This gives an answer of 10^2 cm. I find it hard to fathom how these cut off sections could be twice as big, but apparently they are, if I’m to trust the math of people who remember what I have forgotten. When I found that my answers wasn’t one of the choices, I figured that I must have gotten the area for only ONE of the slices. So I chose the answer that was double, and got it right. That, apparently, was just dumb luck, though.
3.14 25 (1-0.468) + (1.5*sqrt(11) = 20.002
The exact solution is 6 sqrt(11). The limits for the integration must be the x-values of the intersection of the two circles, i.e from -3/2 sqrt(11) to +3/2*sqrt(11). Alan Chan has shown in his solution how these numbers can be obtained. It is somehow surprising that the exact solution contains no Pi at all.
Log in to reply
I think I am slightly mistaken. The points of intersection are not really the limits for the integration, because the upper circle still bends a little beyond that area. Actually the function of the upper circle ist only unique when -5 < x < +5.
Put both circles in a coordinate plane. Let the two circles be C 1 : x 2 + y 2 = 2 5 and C 2 : x 2 + ( y − 1 ) 2 = 2 5 respectively. P and Q are the two points where the circles intersect.
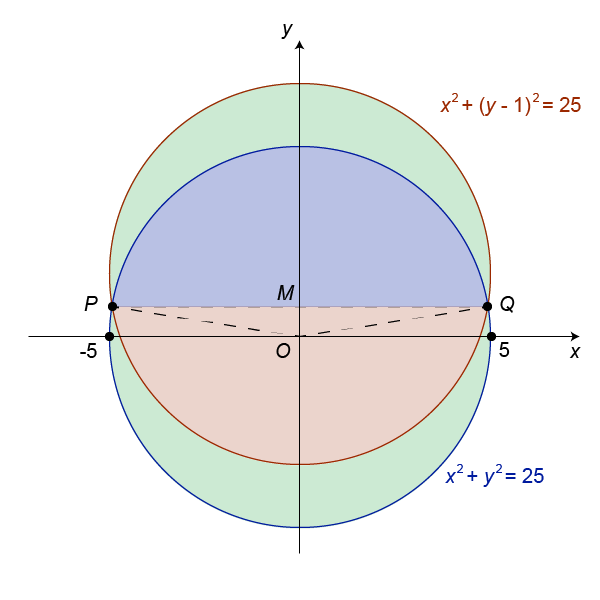
To find P and Q , solve the two simultaneous equations of C 1 and C 2 . We get
y 2 = ( y − 1 ) 2
y = 0 . 5
Put y = 0 . 5 into the equation of C 1 and we get x = ± 2 3 1 1 .
So P = ( − 2 3 1 1 , 0 . 5 ) and Q = ( 2 3 1 1 , 0 . 5 ) .
M is the point where P Q intersects with the y-axis.
Area of triangle POQ = 2 1 ( O M ) ( P Q ) = 2 1 ( 2 5 2 − 0 . 5 2 ) ( 0 . 5 ) = 4 3 1 1
cos ∠ P O M = 5 0 . 5 = 0 . 1
∠ P O M = 8 4 . 2 6 1 ∘ (to 5 sig. fig.)
Hence ∠ P O Q = 8 4 . 2 6 1 ∘ × 2 = 1 6 8 . 5 2 ∘
For C 2 , area of sector O P Q = 5 2 π ( 3 6 0 ∘ 1 6 8 . 5 2 ∘ ) = 3 6 . 7 6 5 (to 5 sig. fig.)
Hence area of segment P M Q = 3 6 . 7 6 5 − 4 3 1 1 = 3 4 . 2 7 8 (to 5 sig. fig.)
We can easily deduce that the blue area is equal to the red area marked in the diagram. The blue area = 5 2 π − 3 4 . 2 7 8 = 4 4 . 2 6 2 (to 5 sig. fig.)
The green area = 2 × ( 4 4 . 2 6 2 − 3 4 . 2 7 8 ) = 2 0 .
Perfect illustration thanks
It seems to me that PMQ is the blue area, i.e. blue area = 34.278. As blue area = red area, this means one green area = 25pi - 2(34.278)=9.9838. Both green areas = 2 x 9.9838=19.967 or approx. 20
I think you have too much "approximately" that it changed the correct solution, i calculate it near 19.... I don't know...
Log in to reply
How did you calculate that?
Log in to reply
I used intergral. The below circle's Center is O(0;0) and the upper circle's Center is O'(0;1). Write down the equation of each circle and find the intersection. I use phone and i can't code latex if you guys want the full solution, give me your email ^^ i I'll send it.
I calculate it with casio fx570vnplus
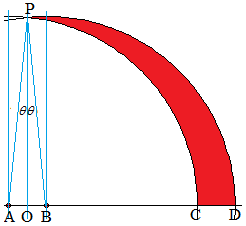
Consider the first quadrants of the two circles. Let A and B be the centers of the two circles, therefore, A B = 1 , and A C = 5 and B D = 5 be their radius on the x -axis. Point P is where the two circles intersect and O be the mid-point of A B . By symmetry, O P is perpendicular to A B .
The shaded area [ P C D ] ( [ ⋅ ] denotes the area) is given by:
[ P C D ] ⟹ A = [ O P D ] − [ O P C ] = [ B P D ] + [ O P B ] − ( [ A P C ] − [ O P A ] ) = 2 5 2 ( π + θ ) + 2 5 2 sin θ cos θ − 2 5 2 ( π − θ ) + 2 5 2 sin θ cos θ = 2 5 ( θ + sin θ cos θ ) = 2 5 ( sin − 1 0 . 1 + 0 . 1 1 − 0 . 1 2 ) = 4 × 2 5 ( sin − 1 0 . 1 + 0 . 1 1 − 0 . 1 2 ) ≈ 1 9 . 9 6 7 ≈ 2 0 Note that sin θ = 5 2 1 = 0 . 1 to the nearest integer
This approach deserves more voting!!! Nice.
very nice solution!
For an approximate answer,we can ignore the detail that the shapes are circles. We have 2 arcs, with a uniform gap of 1cm (in the y direction), and a width (in the x direction) of 10cm.
Total area between the arcs = 1*10 = 10cm2
Total red area = 20cm2
That's what I did
Do it yourself while reading solution.
Take both circles on coordinate axis such that the centre of a circle is at (0,5) and other at (0,6).
Equation of first circle will be x²+(y-5)²=25 Equation of first circle will be x²+(y-6)²=25
Subtract both equations and you will get y=11/2 Putting value of y in one of the equations we get x=(3√11)/2
Now the area of that region will be 4× integral of (√(25-x²) + 6) - (√(25-x²) + 5) from 0 to (3√11)/2 Which is equal to 6√11=19.899≈20
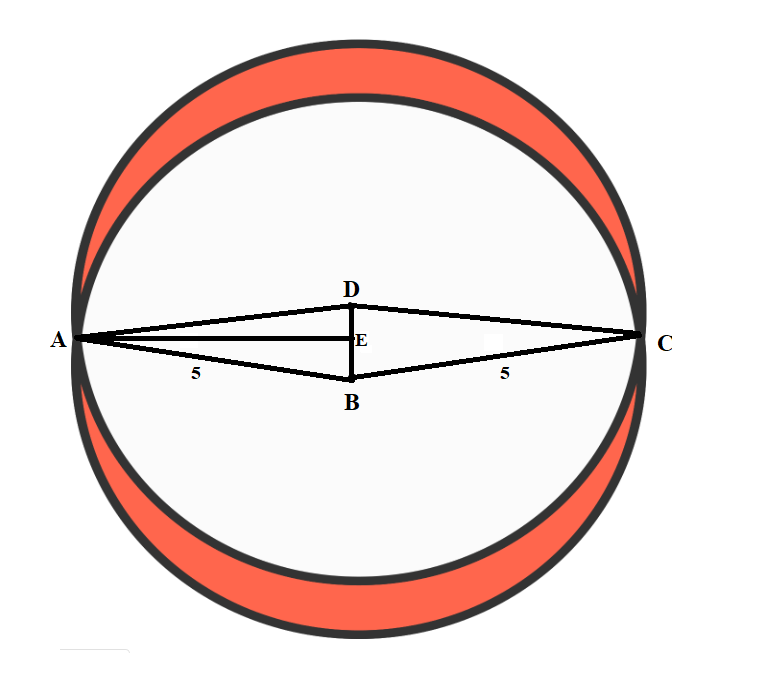
In the above diagram, let points A , E , and C be collinear. △ A B C and △ A D C are congruent isosceles triangles, implying that A B D C is a rhombus, so A E bisects B D . Since B D = 1 , B E = 2 1 .
Let ∠ A B C = θ . Then:
∠ A B E = 2 θ ⟹ cos 2 θ = 5 2 1 = 1 0 1 1 0 1 = 2 cos θ + 1 cos θ = − 5 0 4 9
The area of sector A B C is 2 2 5 θ . A E = 2 5 − 4 1 = 2 3 1 1 , so the area of △ A B C is 4 3 1 1 . The area of the white region is twice the difference between sector A B C and △ A B C , which is 2 ( 2 2 5 θ − 4 3 1 1 ) = 2 5 θ − 2 3 1 1 . Therefore, the area of one red region is 2 5 π − ( 2 5 θ − 2 3 1 1 ) . The total red area is 2 ( 2 5 π − ( 2 5 θ − 2 3 1 1 ) ) = 5 0 π + 3 1 1 − 5 0 arccos − 5 0 4 9 ≈ 1 9 . 9 6 7 , which is 2 0 cm 2 to the nearest square centimeter..
Because of the symmetry, let's just focus on a quarter of the circle, the top right quarter, say. Let's also centre one circle at origin.
To get the second circle, we'll shift the first up one centimeter. The area added when doing this is actually near the x-axis, though it is also exactly one quarter of the red area pictured in the question.
The new area is 1cm high, 5cm wide at the x-axis and still nearly 5cm wide at the top. Using a rectangular approximation. The red area would then be nearly 20cm 2 .
How nearly? Well, the real length of the top edge is 2 4 ≈ 4 . 8 9 9 . Even if we take a linear approximation, the error in the estimate is just over 0.25cm 2 .
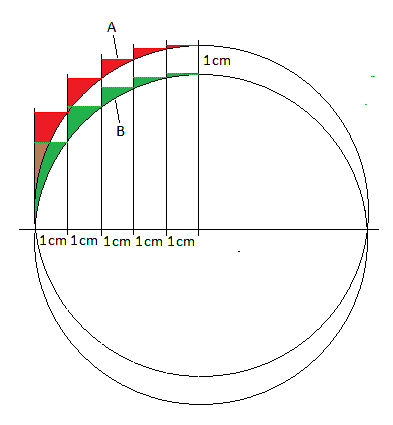 Divide the top left-hand quadrant into 5 columns by vertical lines 1cm apart. Except in the far left column, the red parts have the same area as the green parts below them (for example A and B). In these columns the area between the circles (the green plus the white part) is equal to a square of area 1 square centimetre (the red plus the white part). In the far left column there is a small difference in the area of the red and green parts (which can be made clear by examining the case of a greater distance between the circles). There are five squares in a quadrant and four quadrants, so taking into account the small differences in the outside columns, the area of the two red coloured regions in the original diagram is approximately 20 square centimetres.
Divide the top left-hand quadrant into 5 columns by vertical lines 1cm apart. Except in the far left column, the red parts have the same area as the green parts below them (for example A and B). In these columns the area between the circles (the green plus the white part) is equal to a square of area 1 square centimetre (the red plus the white part). In the far left column there is a small difference in the area of the red and green parts (which can be made clear by examining the case of a greater distance between the circles). There are five squares in a quadrant and four quadrants, so taking into account the small differences in the outside columns, the area of the two red coloured regions in the original diagram is approximately 20 square centimetres.
The upper circle (U) represents a translation of the lower circle (L) upwards by 1 cm. Therefore, every point (u) on U has a corresponding origin point (l) on L, and it is connected to that by a 1 cm line segment ul.
If you then translated all of the line segments from the lower half of U so that their tops are aligned vertically with the center of the lower circle and translate the line segments from the upper half of U so their bottoms aligned with this point, they would form a rectangle 10 cm wide, by 2 cm tall, with an area of 20 cm^2.
This estimate is a bit high because there is a small gap on the left and right of the figures outside the intersection point of the two circles that is excluded in the figure, but included in the approach listed here. That difference is << 1 cm^2.
This solution does not involve any calculus or coordinations.
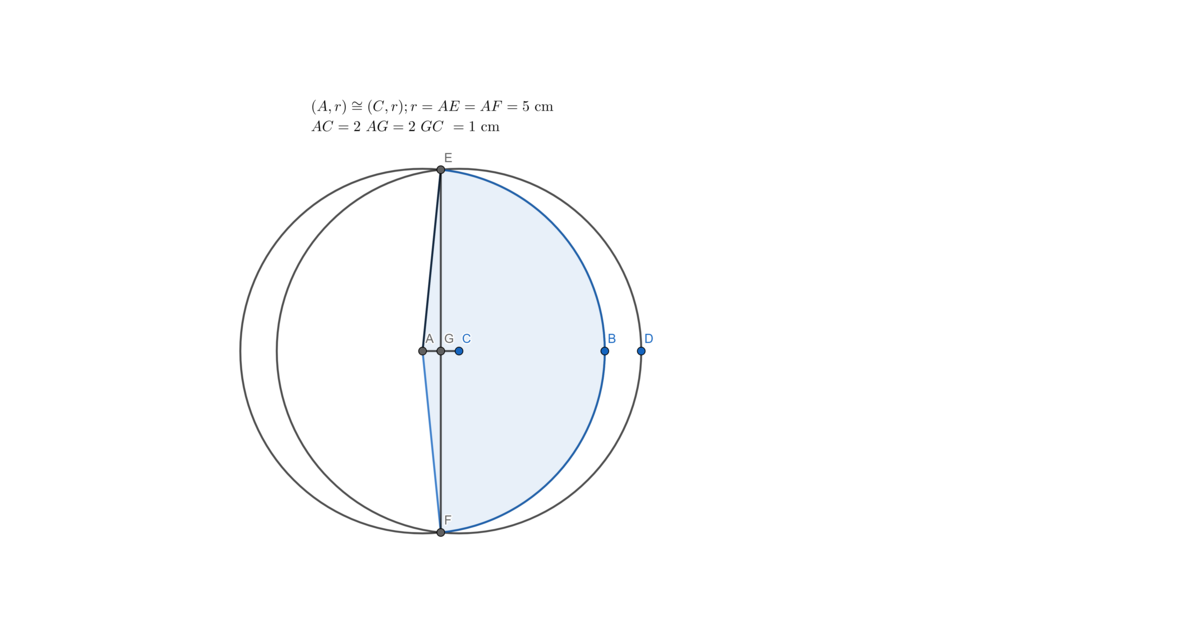
The region in question is calculated by subtracting the area of the circle A and the arc segment E B F , and multiplying the results by 2.
First, we calculate the angle ∠ E A F
∠ E A F = 2 ∠ E A G = 2 arccos A E A G = 2 arccos 1 0 1
And also its sine:
sin ∠ E A F = 2 sin ∠ E A G cos ∠ E A G = 2 1 − cos 2 ∠ E A G × 1 0 1 = 2 1 − ( 1 0 1 ) 2 = 5 0 3 1 1
From this, the area of arc segment E B F can be calculated:
Area of arc segment EBF = 2 r 2 ( ∠ E A F − sin ∠ E A F ) = 2 r 2 ( 2 arccos 1 0 1 − 5 0 3 1 1 )
Half of the red-shaded region (as in the original picture) can be calculated by subtracting two times the arc segment EBF from the area of the circle A:
Half area of red shaded region = Area of circle A − 2 × Area of arc segment EBF = r 2 ( π − 2 arccos 1 0 1 + 5 0 3 1 1 )
Doubling the result gives the necessary value:
Total area of red shaded region = 2 r 2 ( π − 2 arccos 1 0 1 + 5 0 3 1 1 ) ≈ 1 9 . 9 6 6 6 ( cm 2 )
I used basic geometry and found
Area=2[25π-∆/90*25π+3√11/2]
* cos∆=1/10 and ∆ is an acute angle, measured in sexagesimal system
The simplest thought process is to consider two superimposed half circles. One is moved down by 1cm. The diameter is 10cm, giving a non-superimposed area of 10cm^2. This lower area between the two diameters has to be equivalent to the area within the circumference perimeters to balance the displacement on either side of the half circles. Therefore the total non-superimposed area of the two circles is very close to 20cm^2.
No calculus, programming or even surds needed.

My old drawing program doesn't work on Windows 10. When I have a program that works, I'll submit a better drawing.
Edit: Slightly better drawing attached, and nomenclature error corrected
My solution using Monte Carlo approximation in Python (the code could be a lot better but it does the job).
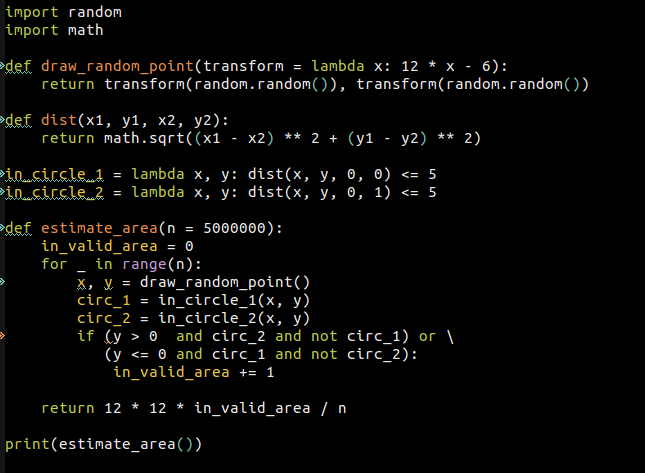
Area of red region = 8 ⋅ ∫ 0 2 1 2 5 − y 2 d y = 1 9 . 9 6 6 6 1 6 c m 2 ≈ 2 0 c m 2 .
One way to simplify the problem is to shift one circle up by 0.5cm, and another circle down by 0.5cm. This makes the integral much easier than putting one circle at the origin and the other 1cm up. The two equations are:
x
2
+
(
y
−
0
.
5
)
2
=
5
2
x
2
+
(
y
+
0
.
5
)
2
=
5
2
or solving for y, we get :
y
t
o
p
=
5
2
−
x
2
+
0
.
5
y
b
o
t
t
o
m
=
5
2
−
x
2
−
0
.
5
Now, the intersection between the two circles is on the x-axis. Setting y = 0 in the first two equations, the intersection occurs at x = 5 2 − 0 . 5 2 . The integral from x = 0 to x = 5 2 − 0 . 5 2 of y t o p − y b o t t o m gives a quarter of total area we are looking for. You can see now why it was so nice to shift each circle by 0.5cm: the integrand simply becomes 1:
\frac{A}{4} = \int_0^\sqrt{5^2 - 0.5^2} (y_{top} - y_{bottom}) dx\ = \int_0^\sqrt{5^2 - 0.5^2} 1 dx = \sqrt{5^2 - 0.5^2}
So the total area we are looking for is
A = 4 5 2 − 0 . 5 2 c m 2 ≈ 2 0 c m 2
You can solve it computationally by approximating the area of the shape with really small squares; whether a point is inside the shape is determined by the first circle boolean field function XOR'd with that of the second circle.
More exact solutions would involve integrals and the equation for a circle.
Let the origin of coordinates (0,0) be the center of the lower circle, then (0,1) are the coordinates of the upper circle. The equations for each circle are: lower circle is x^2 + y^2 = 25. The upper circle has an equation x^2 + (y - 1)^2 = 25. We determine the coordinates of the intersection of the two circles by equating y^2 to (y - 1(^2, or y^2 = y^2 - 2y + 1, and y = 1/2. Substituting y = 1/2 into either equation results in x^2 + 1/4 = 25 = 100/4, so x^2 = 9*11/4, and x = +(3/2)sqrt(11) and x = -(3/2)sqrt(11). Now consider the shaded area of the upper right quadrant. The are is the integral from x = 0 to x = (3/2)sqrt(11) of y(upper) - y(lower), or sqrt(25 - x^2) + 1 - sqrt(25 - x^2) = 1, so the integral is x evaluated from 0 to (3/2)sqrt(11) = 4.974937. This would seem to be 1/4 of the total shaded area by symmetry, so the total is 19. 899, or rounded off, = 20. Ed Gray

Imagine how the parallelogram area formula A = b ⋅ h is derived from skewing a rectangle. Well these red regions are the same thing (except for a tiny bit at the ends.) Skew them to rectangles that are 10 cm wide and 1 cm high and the total area is 1 0 × 1 × 2 = 2 0
The error is less than 0 . 0 5 c m 2 but finding that should be its own problem.
Edit: Finding this error is now its own problem .