Find the Area... Only Your Logic Can Help You...

area =(40^2 -20^2) / 4

hence the answer is 300

simple......and logical.......

Extend $BC$ to meet $AD$ at $F$ , then because $\angle A + \angle B = 90^{\circ}$ , it follows that $\triangle AFB$ and $\triangle DFC$ are right triangles. Now, let $AD = BC = c$ , $CF = z$ , and $AF = w$ , then by applying Pythagorean theorem to $\triangle AFB$ and $\triangle DFC$ , we obtain,

$40^2 = (c + z)^2 + w^2$ , and

$20^2 = z^2 + (c - w)^2$

Subtract,

$1600 - 400 = 1200 = 2 c z + 2 c w = 2 c (z + w)$

Now, the area is given by,

$\text{Area} = \frac{1}{2} w (c + z) + \frac{1}{2} z (c - w ) = \frac{1}{2} c (w + z) = \frac{1}{4} (1200) = 300$

If you extend BC to intersect AD at point E, then you find the segments are perpendicular, so that the figure is divided into two right triangles. Let AE = r and DE = t. By the Pythagorean Theorem, CE = $\sqrt{400-t^2}$ . Therefore, the area of the two triangles is given by $\frac{1}{2} (r(r+t+\sqrt{400-t^2})+t\sqrt{400-t^2})$ . By applying the Pythagorean Theorem to $\Delta$ ABE, $r^2+(r+t+\sqrt{400-t^2})^2=1600$ . This can be easily manipulated to obtain $\frac{1}{2} (r(r+t+\sqrt{400-t^2})+t\sqrt{400-t^2})=300$ .

Take angle A =45 and angle B = 45 , then the figure transforms into trapezium , then we have to just calculate the area of trapezium

Using the fact that $AD = BC$ , we can construct three copies of figure $ABCD$ and orient them as such:

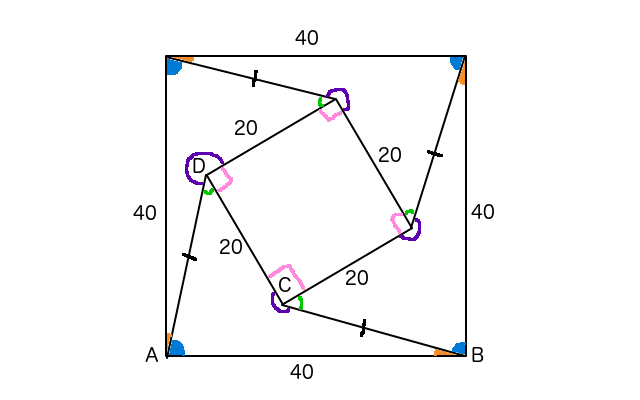
Thus, we have a large figure comprised of four copies of $ABCD$ and another quadrilateral in the middle (with the four pink angles). The strategy becomes clear - if we can find the area of the large figure and the smaller quadrilateral, we can subtract the two to find the area of the copies, with the area of the original easily being derived from that.

We're given that $m\angle A + m\angle B = 90$ (the angles are blue and orange, respectively in each copy); since the large figure has four 90-degree angles and four sides of equal length, it is a square, and its area is 1600.

Looking at the center of the large figure, we can see the green, purple, and pink angles all intersect at a single point, thus $m\angle green + m\angle purple + m\angle pink = 360.$

From the original figure, we know $m\angle blue + m\angle orange = 90$ which holds for the copies, so then $m \angle green + \angle purple = 270$ and $m \angle pink = 90.$ The interior figure has four 90-degree angles and four sides of equal length so it is a square as well, and its area is 400.

Thus, Area(4 copies of ABCD) = Area(large square) - Area (small square) = 1600 - 400 = 1200. It follows that the area of one form of $ABCD$ is 300 .

Let the angle B be 0. we will have a right angle triangle with height AB(let it be x), base AC which will be 40-x, and hypotenuse DC=20. Now solve for x, Find the area of the right angle triangle.

Let C=180º. Then, you have a triangle with angles A, 90-A and 90. Let x=AD so that the side DB=20+x. Then, applying the Pythagorean theorem to triangle ADB, you get to the second degree equation $2x^2+40x-1200$ with the positive root $x = 10 (\sqrt{7} - 1)$ .

The area is given by $A=\frac{(\sqrt{7} - 1)(20+(\sqrt{7} - 1))}{2}=300$

First time writting a solution and using latex so there might be some mistakes in the writing.