Integrating mixture of functions

Relevant wiki: Differentiation Under the Integral Sign

Proposition :

$\large{\displaystyle \int_{0}^{\infty} \frac{\cos mx}{x^2+a^2} \mathrm{d} x=\frac{\pi}{2a} e^{-am}}$

Proof :

$\text{I}(m) = \displaystyle \int_{0}^{\infty} \dfrac{\cos mx}{x^2+a^2} \mathrm{d} x \tag{1}$

Using Integration by parts,

$\text{I}(m) = \displaystyle \int_{0}^{\infty} \dfrac{2x\sin mx}{m(x^2+a^2)^2} \mathrm{d} x$

$\implies m \cdot \text{I}(m) = \displaystyle \int_{0}^{\infty} \dfrac{2x \sin mx}{(x^2+a^2)^2} \mathrm{d} x \tag {2}$

Partially Differentiating $(2)$ w.r.t. $m$ , we have,

$\text{I} + m\dfrac{\partial}{\partial m} \text{I} = \displaystyle \int_{0}^{\infty} \dfrac {2x^2\cos(mx)}{(x^2+a^2)^2} \mathrm{d}x = \displaystyle \int_{0}^{\infty} \dfrac {2\cos(mx)}{(x^2+a^2)} \mathrm{d}x - 2a^2\displaystyle \int_{0}^{\infty}\dfrac{\cos mx}{(x^2+a^2)^2} \mathrm{d}x$

$\implies m\dfrac{\partial}{\partial m} \text{I} = \text{I} - 2a^2\displaystyle \int_{0}^{\infty}\dfrac{\cos mx}{(x^2+a^2)^2} \mathrm{d}x \tag{3}$

Again, partially differentiating $(3)$ w.r.t. $m$ , we have,

$m\dfrac{\partial^2}{\partial m^2} \text{I} = a^2 \displaystyle \int_{0}^{\infty} \dfrac{2x \sin mx}{(x^2+a^2)^2} \mathrm{d} x$

\implies \dfrac{\partial^2}{\partial m^2} \text{I} = a^2 \text{I} \tag{*} (from $(2)$ )

Note that $I(0) = \dfrac{\pi}{2a}$ and $I(\infty) = 0$

Now, solving $(*)$ , we have,

$I = \dfrac{\pi}{2a} e^{-am}$

---

$\displaystyle \int \limits^{\infty }_{0}\frac{\cos \left( \pi x\right) }{4x^{2}+1} dx = \dfrac{1}{4}\int \limits^{\infty }_{0}\frac{\cos \left( \pi x\right) }{x^{2}+\frac{1}{4}} dx = \dfrac{\pi}{4} e^{-\frac{\pi}{2}}$

$\implies A + B = \boxed{6}$

Relevant wiki: Cauchy Integral Formula

Since the integrand is even, we have $\displaystyle \int_0^\infty \frac {\cos (\pi x)}{4x^2+1} dx = \frac 12 \int_{-\infty}^\infty \frac {\cos (\pi x)}{4x^2+1} dx$ . We can solve this integral by using the closed contour $C$ of a semicircle of radius $R \to \infty$ in the upper half of the complex plane.

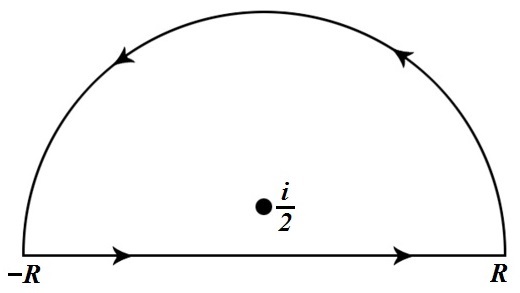
Therefore the integral is as follows:

$\begin{aligned} \int_C \frac {e^{i\pi z}}{4z^2+1} dz & = \int_{-R}^R \frac {e^{i\pi z}}{4z^2+1} dz + \color{#3D99F6} \int_{arc} \frac {e^{i\pi z}}{4z^2+1} dz & \small \color{#3D99F6}\text{Note that }\lim_{R \to \infty} \int_{arc} \frac {e^{i\pi z}}{4z^2+1} dz = 0 \\ & = \int_{-\infty}^\infty \frac {\cos \pi x}{4x^2+1} dx \end{aligned}$

Therefore, we have:

$\begin{aligned} \implies \int_0^\infty \frac {\cos (\pi x)}{4x^2+1} dx & = \frac 12 \int_C \frac {e^{i\pi z}}{4z^2+1} dz \\ & = \frac 18 \int_C \frac {e^{i\pi z}}{z^2 + \frac 14} dz \\ & = \frac 18 \int_C \frac {e^{i\pi z}}{{\color{#3D99F6}\left(z - \frac i2 \right)}\left(z + \frac i2 \right)} dz & \small \color{#3D99F6}\text{Only pole within contour }z = \frac i2 \\ & = \frac 18 \cdot 2\pi i \cdot \frac {e^{i\pi \cdot \frac i2}}{\left(\frac i2 + \frac i2 \right)} dz & \small \color{#3D99F6}\text{By Cauchy integral formula} \\ & = \frac 14 \pi e^{-\frac \pi 2} \end{aligned}$

$\implies A+B = 2+4 = \boxed{6}$

Inside Complex Analysis, supposing known residue theorem...

Proposition 1.-

Let $P,Q$ be polynomials with $\text{ degree (Q) - degree (P)} \ge 1$ . If $f = \frac{P}{Q}$ doesn't have any poles at the real axis, the following improper integral converges and its value is $\displaystyle \int_{- \infty}^{\infty} f(x) \cdot e^{ix} \, dx = 2i\pi \cdot \sum_{Im \space a > 0} \text{ Res(} f(x)\cdot e^{ix},a)$ with $a$ being a pole of $f$ .

Proof .-

(Only if someone asks to me)

Examples.- Let $a, b \in \mathbb{R} \space$ such that $a , b > 0$

$\displaystyle I = \int_{0}^{\infty} \frac{\cos bt}{t^2 +a^2} \, dt = \frac{\pi}{2ae^{ab}}$ $\displaystyle J = \int_{0}^{\infty} \frac{t \sin bt}{t^2 +a^2} \, dt = \frac{\pi}{2e^{ab}}$

Proof.-

$I, J$ are integrals of even functions,

Calculation of I:

$\displaystyle I = \int_{0}^{\infty} \frac{\cos bt}{t^2 +a^2} \, dt = \frac{b}{2}\left( \int_{-\infty}^{\infty} \frac{\cos x}{x^2 +a^2 b^2} \, dx \right) = \frac{b}{2} \left (\text{ Real }\int_{-\infty}^{\infty} \frac{e^{ix}}{x^2 +a^2 b^2} \, dx \right)$ then we are going to apply proposition 1. The only pole of $\frac{e^{ix}}{x^2 +a^2 b^2}$ in the upper-half plane is $z = ab i$ and its residue value is $\frac{e^{-ab}}{2ab i}$ so $\displaystyle \int_{-\infty}^{\infty} \frac{e^{ix}}{x^2 +a^2 b^2} \, dx = 2\pi i \frac{e^{-ab}}{2ab i} = \frac{\pi}{ab e^{ab}} \Rightarrow I = \frac{\pi}{2a e^{ab}}$ . With this we can calculate the above integral, (for instance like Isan Signh did ), this is $A = 2, B = 4$

Calculation of J:

$\displaystyle J = \int_{0}^{\infty} \frac{t \sin bt}{t^2 +a^2} \, dt = \frac{1}{2}\left( \int_{-\infty}^{\infty} \frac{x \sin x}{x^2 +a^2 b^2} \, dx \right) = \frac{1}{2} \left (\text{ Image }\int_{-\infty}^{\infty} \frac{xe^{ix}}{x^2 +a^2 b^2} \, dx \right)$ then we are going to apply proposition 1. The only pole of $\frac{xe^{ix}}{x^2 +a^2 b^2}$ in the upper-half plane is $z = ab i$ and its residue value is $\frac{e^{-ab}}{2}$ so $\displaystyle \int_{-\infty}^{\infty} \frac{xe^{ix}}{x^2 +a^2 b^2} \, dx = 2\pi i \frac{e^{-ab}}{2} = \frac{\pi i}{ e^{ab}} \Rightarrow J= \frac{\pi}{2 e^{ab}} \square$

Proposition 2.- (for Refaat..)

Let $P,Q$ be polynomials with $\text{ degree (Q) - degree (P)} \ge 1$ . If $f = \frac{P}{Q}$ doesn't have any poles at the real axis, except at the origin, where $f$ is able to have a simple pole. Then, $\forall \epsilon > 0$ , the integrals $\displaystyle \int_{- \infty}^{-\epsilon} f(x)\cdot e^{ix} \, dx$ , $\displaystyle \int_{\epsilon}^{\infty} f(x)\cdot e^{ix} \, dx$ converge as $\epsilon \to 0$ , and $\displaystyle \lim_{\epsilon \to 0} \int_{|x| \ge \epsilon} f(x)\cdot e^{ix} \, dx = 2i\pi \cdot \sum_{Im \space a > 0} \text{ Res(} f(x)\cdot e^{ix},a) + i\pi \cdot \text{ Res(} f(x)\cdot e^{ix},0)$

( Proof.- Only if Refaat asks to me, because this proposition is not necessary for this exercise)

Example.-

$\displaystyle \int_{0}^{\infty} \frac{\sin t}{t} \, dt = \frac{\pi}{2}$

Proof.-

Applying proposition 2, $\text{ Res (} \frac{e^{ix}}{x}, 0) = 1 \Rightarrow$ $\displaystyle \int_{-\infty}^{\infty} \frac{e^{ix}}{x} \, dx = \pi i \Rightarrow \int_{0}^{\infty} \frac{\sin x}{x} \, dx = \frac{\pi}{2}$

For variety... Taking the Fourier transform of the function $f(x) = e^{-\frac12|x|}$ , $(\mathcal{F}f)(t) \; = \; \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}} f(x)e^{-ixt}\,dx \; =\; \frac{1}{\sqrt{2\pi}}\left(\frac{1}{\frac12 + it} + \frac{1}{\frac12 - it}\right) \; =\; \frac{2\sqrt{2}}{\sqrt{\pi}(4t^2+1)}$ and so (the function $f$ is well-behaved for this identity to be true for all $x$ , and not just in the "almost everywhere" sense) $f(x) \; = \; (\mathcal{F}^{-1}\mathcal{F}f)(x) \; =\; \frac{1}{\sqrt{2\pi}}\int_{\mathbb{R}} (\mathcal{F}f)(t)e^{itx}\,dt \; = \; \frac{2}{\pi}\int_{\mathbb{R}}\frac{e^{itx}}{4t^2+1}\,dt$ so that $\int_0^\infty \frac{\cos \pi t}{4t^2+1} \; = \; \tfrac12\int_{\mathbb{R}} \frac{e^{i\pi t}}{4t^2+1}\,dt \; =\; \tfrac14e^{-\frac12\pi}$ making the answer $2+4=\boxed{6}$ .