Find the flux!

I am sure there is a neater way to this problem but I couldn't figure it out so bashed it with the integrals. :S

Consider a point $(x,0,z)$ in the $x,z$ plane. The position of this point wrt $(0,\sqrt{3}a/2,0)$ is given by,

$\displaystyle \vec{r}=x\hat{i}-\frac{\sqrt{3}a}{2}\hat{j}+z\hat{k}$

The electric field at this point due to the charge is given by:

$\displaystyle \vec{E}=\frac{kq}{\left(x^2+\frac{3a^2}{4}+y^2\right)^{3/2}}\left(x\hat{i}-\frac{\sqrt{3}a}{2}\hat{j}+z\hat{k}\right)$

The flux through the specified region is given by:

$\displaystyle \phi=\oint \vec{E}\cdot \vec{dA}=\int_{a/2}^{3a/2} \int_{-\infty}^0 \frac{kq^2}{\left(x^2+\frac{3a^2}{4}+z^2\right)^{3/2}}\left(x\hat{i}-\frac{\sqrt{3}a}{2}\hat{j}+z\hat{k}\right)\cdot \left(dz\,dx\,(-\hat{j})\right)$

$\displaystyle \Rightarrow \phi=\int_{a/2}^{3a/2} \int_{-\infty}^0 \frac{\sqrt{3}akq^2}{2\left(x^2+\frac{3a^2}{4}+z^2\right)^{3/2}}\,dz\,dx$

Solving the above definite integral gives:

$\phi=\boxed{\dfrac{q}{24\epsilon_0}}$

@Gauri shankar Mishra
1)you should take a cuboidal guassian surface.with one side as provide and other a/2<x<3a/2,y=root(3)a/2 and -oo<z<0 i hope you could imagine it.

2) the flux because of this is 0,the one which is at infinity is zero and the other which is parallel to it is zero.also net flux is zero. so difference of flux due to other 2 left will give us the flux due to mentioned surface.

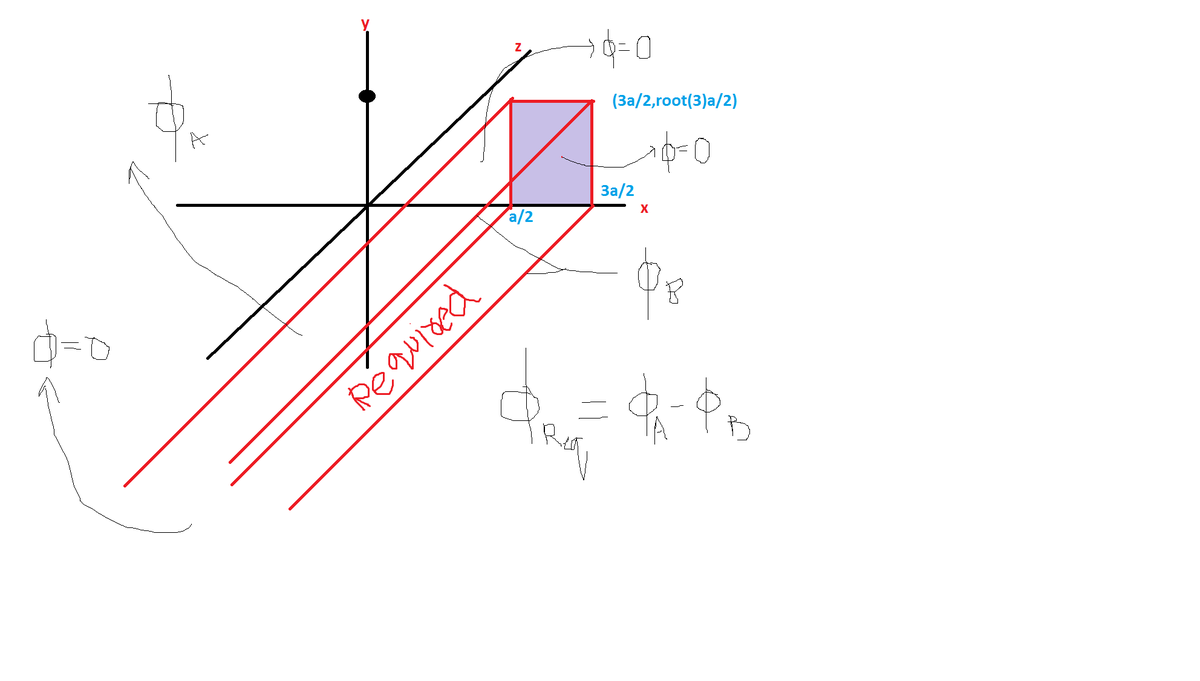
flux(A) can be determined by imagining an equilateral triangular prism .imagining a as half of one side of prism ={q/2e}(1/6)

flux of B by hexagonal prism. .imagining a as half of one side of prism ={q/2e}(1/12) difference =q/24e