Find the length of the tangent
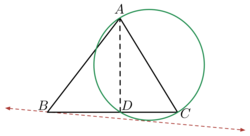ABC
is an acute angle triangle with side
AC=10cm
. A perpendicular is drawn from point
A
on side
BC
that cuts the side
BC
at point
D
. Length of
AD=6cm
.
∠
B
A
D
=
3
0
°
. Then two tangents are drawn from points
B
and
C
to the circumcircle of
ΔACD
&
ΔABD
respectively. Consider those two tangents are
BT
&
CS
respectively. Then find the ratio of
B
C
B
T
×
C
S
The answer is 5.264296052.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
This is a good solution--a lot shorter than my one, which calculates individually the lengths of BT and CS using Stewart's Theorem. The Power of a Point step was very creative.
The identity is BT^2 = BD x BC. The actual answer is about 6.302 cm.
The solution is mistaken. The correct solution is BT BT=BD BC, so BT=6.30181
Sorry !! I commit a mistake to solve this one . I make a little change in the question. Sorry to those whose rating is affected due to me.
Why is the solution 6.30181? I understand the solution but why does my solution yield a different result? Is it because the question has been changed before I did this?
Yeah have done it dat.Got a little frightened when i saw my ans comes down to 4 * 4th root of 3.Having said that now i can go to sleep at peace@4am.
Why is BT^2=BD x DC?
Log in to reply
I got it
Log in to reply
Can you understand my solution?
Log in to reply
@Arghyanil Dey – Yes with the help of my dad I did understand it but I think you should mention the property that you used in the last step😃.
Huh? There is nothing mistaken about the problem. What I did was to use coordinate geometry. Obviously, BD = 2 sqrt(3) and BA = 4 sqrt(3) and CD = 8 (All of these by Pythagoras theorem). Let O be the circumcentre of triangle ADC and P be the circumcentre of triangle ADB. BT = sqrt(BO^2 - OT^2). BO^2 = 37 + 8 sqrt(12) and OT^2 = 25. So BT = 6.301810289. Similarly, we get CS = 9.576680684. BC = 8 + 2 sqrt(3) = 11.46410162. Thus , the required answer is 5.264296049.
I think you mean B T = B O 2 − O T 2 instead of B T = B O 2 − B T 2 . Also, O T 2 = 2 5 instead of B T 2 = 2 5 . Otherwise, this solution is fine.
Thanks for the correction. :)
As ∠ A D C = 9 0 ° hence AC is the diameter of the circumcircle ΔACD . From Pythagorus theorem we can get CD=8cm . As ∠ A D B = 9 0 ° then BD=6tan30=3.464cm . Let the tangent touches the circle at point T .
Then , ( B T ) 2 = B D × B C and C S 2 = C D × B C so the required ratio is nothing but C D × B D