Box Up The Cubic
For a certain value ,
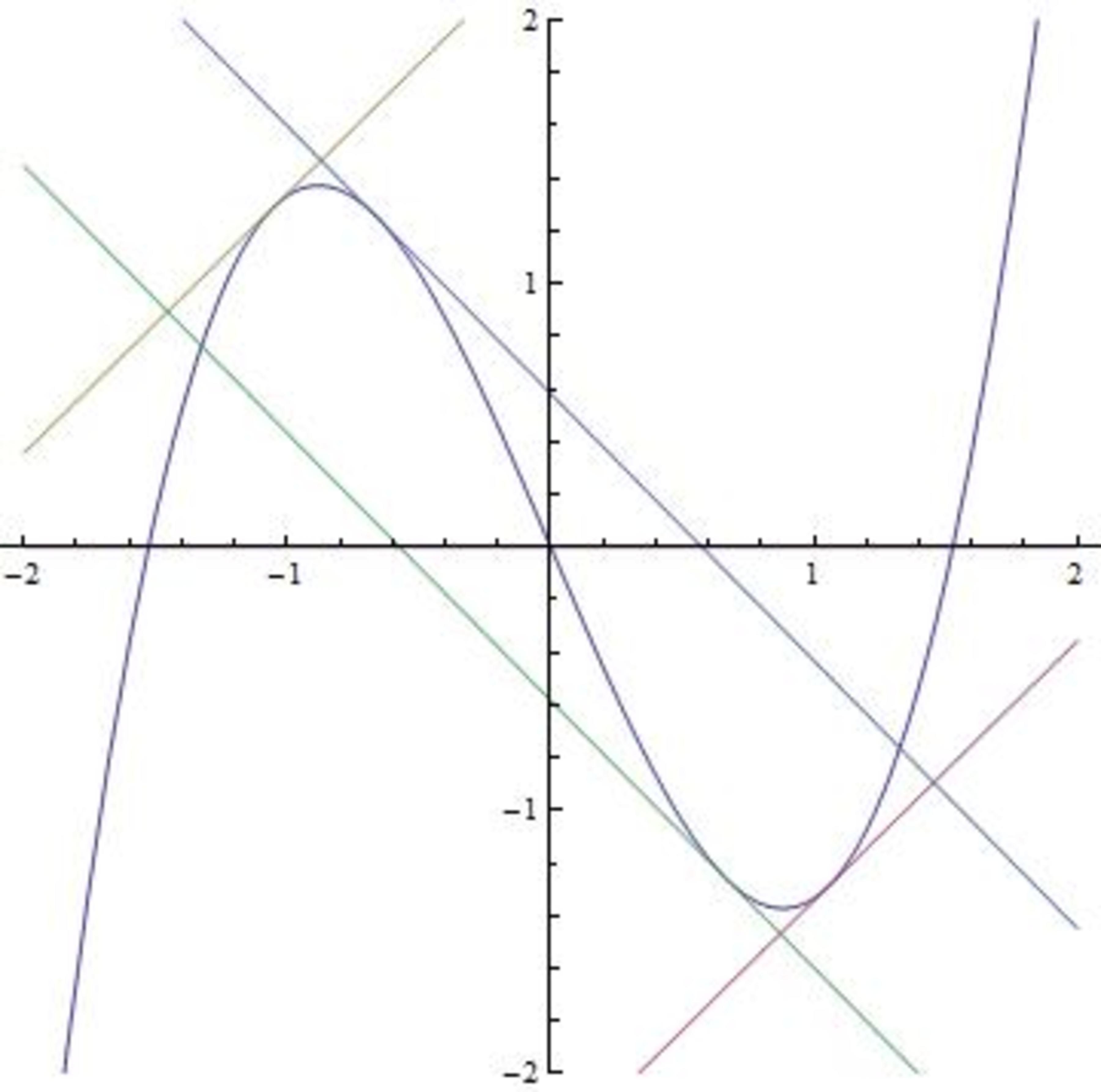
there can be only one box that is tangent on all 4 sides to this cubic . Find the ratio of its sides. (The ratio is a number greater than 1.)
The box is a rectangle, possibly tilted. The cubic curve may pass through the box, but this cubic curve must nevertheless be tangential to all four sides of the box.
Give your answer to 3 decimal places.
Note : The above image is an example of a box tangent on all 4 sides to a cubic. However, this box is not the only one possible for this cubic.
The answer is 4.000.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
We seek to find a box where two of the tangent points are at opposite corners. The equation for the line tangent to x 3 − p x at x = a is ( 3 a 2 − p ) x − 2 a 2 , which intersects the cubic at x = − 2 a . The equation for the line tangent to x 3 − p x at x = − 2 a is ( 1 2 a 2 − p ) x + 1 6 a 2 . For a box to be formed, then, the slopes of the tangent lines must be orthogonal, which is true if ( 3 a 2 − p ) = − ( 1 2 a 2 − p ) − 1 , which is true if a = ± 2 6 1 5 p ± 9 p 2 − 1 6 . An unique solution exists only if 9 p 2 − 1 6 = 0 , or p = 3 4 . From this,the ratio of the sides of the box can eventually be worked out to be exactly 4 . For p < 3 4 , no box is possible where all of the tangent points are confined to its 4 sides. For p > 3 4 , more than one such box is possible.