Find the remainder
Is 8 2 0 4 8 − 6 2 0 4 8 divisible by 700?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
How do you prove it is divisible by 100 as well?
who will prove it divisible by 100??
Log in to reply
The original problem I read was only divisible by 7. See Vicky Vignesh's solution.
Log in to reply
i have solved it before him
Log in to reply
@Nivedit Jain – I solved it earlier but did not provide solution. I only provided solution after seeing her solution. I didn't see any other solution. I have provided the solution for divisible by 700.
Log in to reply
@Chew-Seong Cheong – i know sir i just commented that in fun
Log in to reply
@Nivedit Jain – It is quite okay. We all are serious about math.
I have provided a new solution.
oh! awesome one
Apply the formula a^2n - b^2n = (a^n - b^n) (a^n + b^n) repeatedly until the power of 8 and 6 is 1. 2048 = 2^20.
8^2048 - 6^2048 = (8^1024 - 6^1024) * (8^1024 +6^1024) = (8^516 - 6^516) * (8^516 + 6^516) * (8^1024 +6^1024) = (8^256 - 6^256) * (8^256 - 6^256) *(8^516 + 6^516) * (8^1024 +6^1024) ..... = (8^2 - 6^2) * (8^2 +6^2) * ... * (8^256 - 6^256) *(8^516 + 6^516) * (8^1024 +6^1024) = (8 - 6) * (8 + 6) * (8^2 +6^2) * ... * (8^256 - 6^256) *(8^516 + 6^516) * (8^1024 +6^1024)
8+6 =14 (8^2 +6^2) = 64 + 36 = 100
2, 7, 100 are factors of 8^2048 - 6^2048 Therefore 700 divides 8^2048 - 6^2048
We have:
8 2 0 4 8 − 6 2 0 4 8 ≡ 0 − 2 2 0 4 8 ⋅ 3 2 0 4 8 ≡ − 4 1 0 2 4 ⋅ 3 2 0 4 8 ≡ 0 ( m o d 4 )
8 2 0 4 8 − 6 2 0 4 8 ≡ 1 2 0 4 8 − ( − 1 ) 2 0 4 8 ≡ 1 − 1 ≡ 0 ( m o d 7 )
8 2 0 4 8 − 6 2 0 4 8 ≡ 2 6 1 4 4 m o d ϕ ( 2 5 ) − 6 2 0 4 8 m o d ϕ ( 2 5 ) ≡ 2 6 1 4 4 m o d 2 0 − 6 2 0 4 8 m o d 2 0 ( m o d 2 5 ) ≡ 2 4 − 6 8 ≡ 1 6 − 1 1 4 ≡ 1 6 − 2 1 2 ≡ 1 6 − 1 6 ≡ 0 ( m o d 2 5 )
So, 8 2 0 4 8 − 6 2 0 4 8 ≡ 0 ( m o d 7 0 0 ) , and we conclude that 8 2 0 4 8 − 6 2 0 4 8 is divisible by 7 0 0 .
8 2 0 4 8 − 6 2 0 4 8 = 2 3 × 2 0 4 8 − 2 2 0 4 8 × 3 2 0 4 8 = 2 2 0 4 8 [ 2 2 × 2 0 4 8 − 3 2 0 4 8 ] Now we eliminate all a n + b n as they won’t simply be said to divide 7. We’ll take and reduce all numbers of the form a n − b n = 4 2 0 4 8 − 3 2 0 4 8 = ( 4 1 0 2 4 + 3 1 0 2 4 ) ( 4 1 0 2 4 − 3 1 0 2 4 ) 2 0 4 8 = 2 × 1 0 2 4 = 4 5 1 2 − 3 5 1 2 1 0 2 4 = 2 × 5 1 2 = 4 2 5 6 − 3 2 5 6 5 1 2 = 2 × 2 5 6 = 4 1 2 8 − 3 1 2 8 2 5 6 = 2 × 1 2 8 = 4 6 4 − 3 6 4 1 2 8 = 2 × 6 4 = 4 3 2 − 3 3 2 6 4 = 2 × 3 2 = 4 1 6 − 3 1 6 3 2 = 2 × 1 6 = 4 8 − 3 8 1 6 = 2 × 8 = 4 4 − 3 4 8 = 2 × 4 = 4 2 − 3 2 4 = 2 × 2 ⟹ ( 4 + 3 ) ( 4 − 3 ) ⟹ 7 ∗ 1 = 7
Even simpler using congruency.
8 ≡ 1 ( m o d 7 ) 8 2 0 4 8 ≡ 1 2 0 4 8 ≡ 1 ( m o d 7 ) 6 ≡ − 1 ( m o d 7 ) 6 2 0 4 8 ≡ − 1 2 0 4 8 ≡ 1 ( m o d 7 ) 8 2 0 4 8 − 6 2 0 4 8 ≡ 1 − 1 = 0 ( m o d 7 ) ∴ 7 ∣ ( 8 2 0 4 8 − 6 2 0 4 8 )
Can you show why it is divisible by 100 as well?
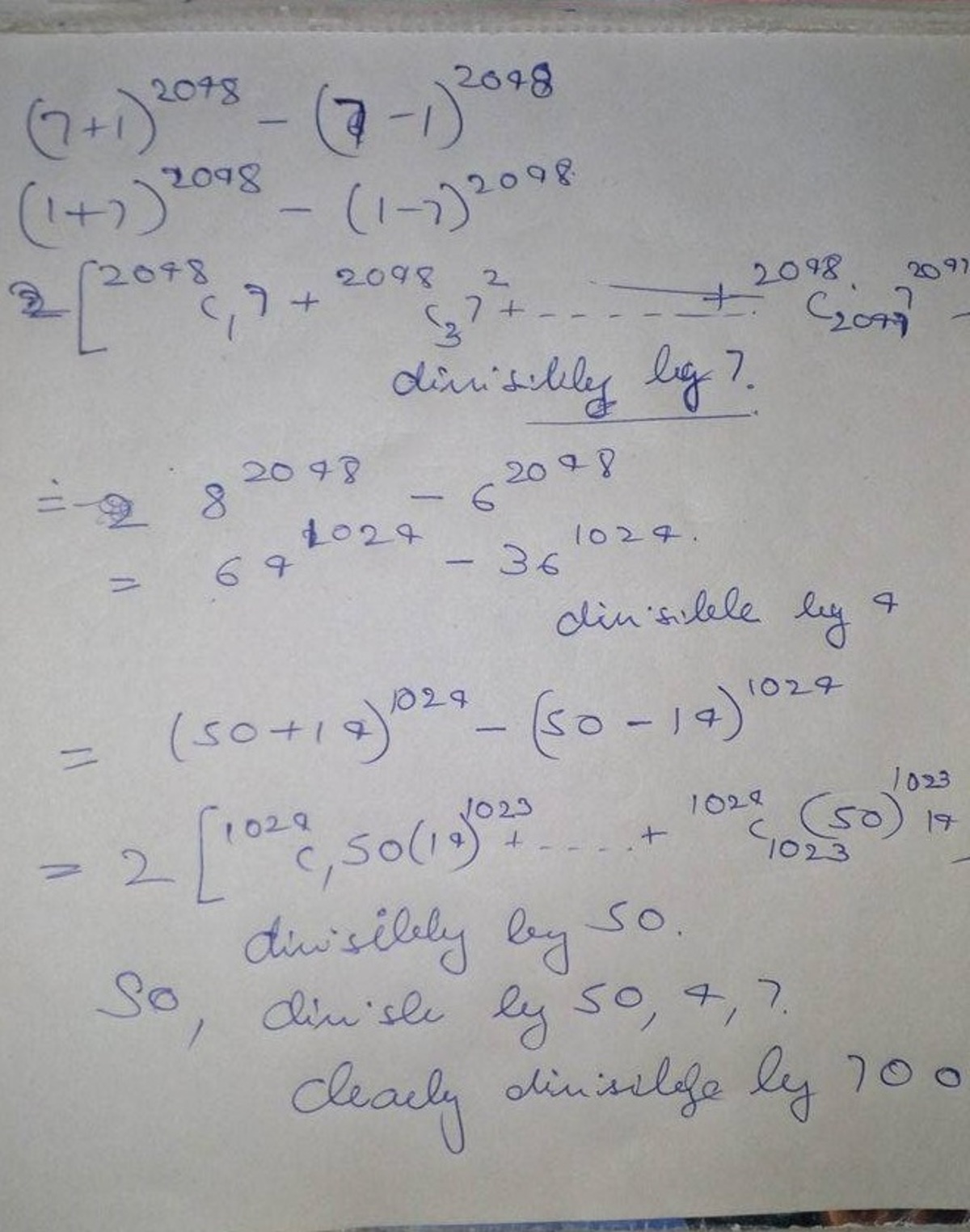
8 2 0 4 8 − 6 2 0 4 8 = ( 8 1 0 2 4 − 6 1 0 2 4 ) ( 8 1 0 2 4 + 6 1 0 2 4 ) (mod 700) = ( 8 5 1 2 − 6 5 1 2 ) ( 8 5 1 2 + 6 5 1 2 ) ( 8 1 0 2 4 + 6 1 0 2 4 ) (mod 700) = ( 8 2 5 6 − 6 2 5 6 ) ( 8 2 5 6 + 6 2 5 6 ) ( 8 5 1 2 + 6 5 1 2 ) ( 8 1 0 2 4 + 6 1 0 2 4 ) (mod 700) = ( 8 − 6 ) ( 8 + 6 ) ( 8 2 + 6 2 ) ( 8 3 + 6 3 ) . . . ( 8 1 0 2 4 + 6 1 0 2 4 ) (mod 700) = ( 2 ) ( 1 4 ) ( 1 0 0 ) ( 8 3 + 6 3 ) . . . ( 8 1 0 2 4 + 6 1 0 2 4 ) (mod 700) = 0 (mod 700)
Yes , 8 2 0 4 8 − 6 2 0 4 8 is divisible by 700.