Find the sides of this triangle.
The sides of a triangle are in an arithmetic progression, and the greatest angle of the triangle is double the smallest angle.
The ratio of the three sides can be expressed as a : b : c , where a , b , c are coprime positive integers.
What is a + b + c ?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
This is what i dont get... maybe my definition of coprime is wrong, but 4,5, and 6 arent coprimes since 6 and 4 are bith divisible by 2...
Log in to reply
4 and 6 as a pair are coprimes. But 4,5 and 6 are not. There is no common divisor for the the three numbers.
I thought the same as Little Narwhal. Both 6 and 4 are divisible by 2. Stumped me for ages.
For △ A B C , suppose D is the intersection point of BC and the angle bisector of A. As the lengths of AC, AB and BC are in an arithmetic progression, assume A C = a − d , A B = a , B C = a + d
∵ △ A C B ∼ △ D A B ( A A A ) ∴ A C D A = C B A B = A B D B ( c o r r . s i d e s , ∼ △ s ) Then we have, a A D = a + d a − d = a − d D B Also, we know that C D = A D ( b a s e ∠ s , i s o s . △ )
Finally, consider the length of BC, we have, a ( a + d a − d ) + a + d ( a − d ) 2 = a + d a ( a − d ) = ( a + d ) 2 − ( a − d ) 2 a = 5 d ( ∵ a = 0 ) Therefore, A C : A B : B C = 4 : 5 : 6
draw A D that bisect ∠ B A C , Δ A B C ∼ Δ D B A
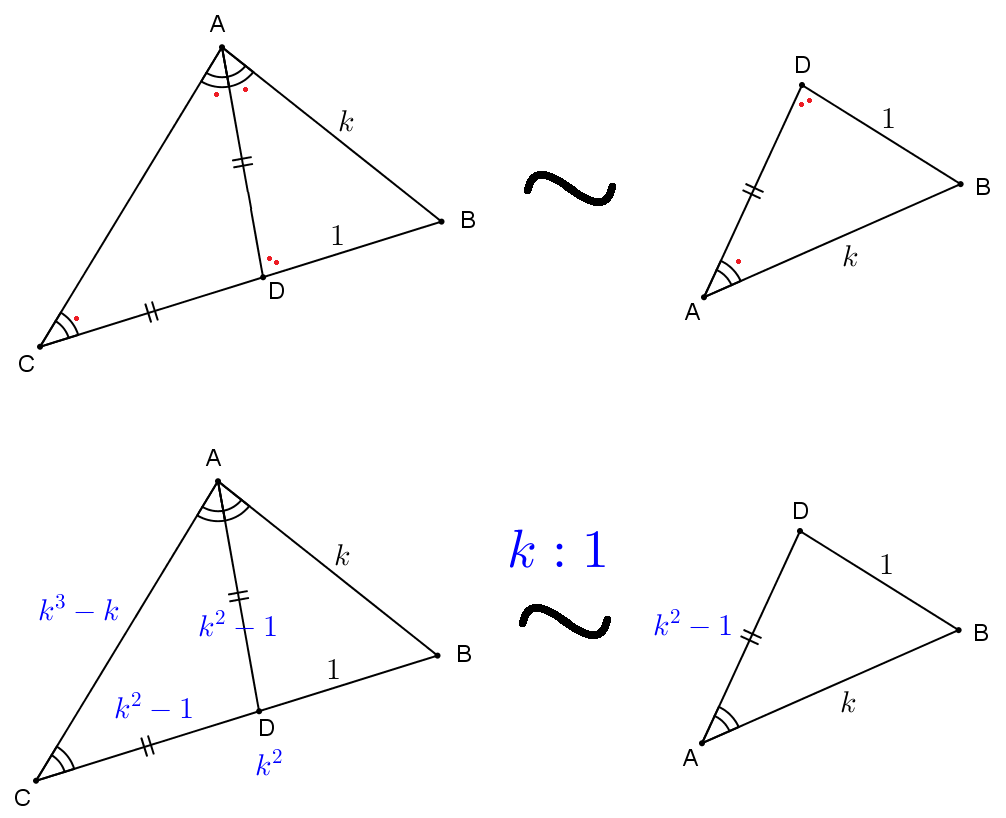
use sides 1 , k , k 2 − 1 from Δ D B A to form an arithmetic progression ( a + c = 2 b and 2 other permutations), solve for k
k = − 1 , 2 3 , 0 , 2 , 2 − 1 ± 1 3
k = 2 3 is the only reasonable solution, which work out to be 4 : 5 : 6
edit: only one permutation possible, read replies.
There are “no other permutations”. The longest side is k 2 and the shortest side is k , so we have 2 ( k 3 − k ) = k 2 + k , so k = − 1 , 0 , 2 3 only.
Log in to reply
k^3-k could be longest? or shortest? i mean i cant "immediately" know k^3-k or k^2 is longer.
in fact there are solution (k=2) for k^3-k to be longest, which form a straight line, and rejected. i certainly cant tell from the start.
Log in to reply
Yes you can, since you have determined which the smallest and largest angles are, and the longest side is opposite the largest angle, and the shortest side opposite the smallest angle.
Log in to reply
@Mark Hennings – oops i missed the word smallest and greatest angle from the question, my bad. i'll leave my mistakes in.
on the plus side, i manage to prove that without the condition " smallest and greatest angle" , this is still the only possible solution.
Let C = θ , A = 2 θ , B = 1 8 0 − 3 θ .
sin 2 ( 2 θ ) − sin 2 ( θ ) = sin ( 1 8 0 − 3 θ ) sin ( θ )
a 2 − c 2 = b c
As a + c = 2 b we get c a = 2 3 .
Thus, a : b : c = 6 : 5 : 4
6 + 5 + 4 = 1 5
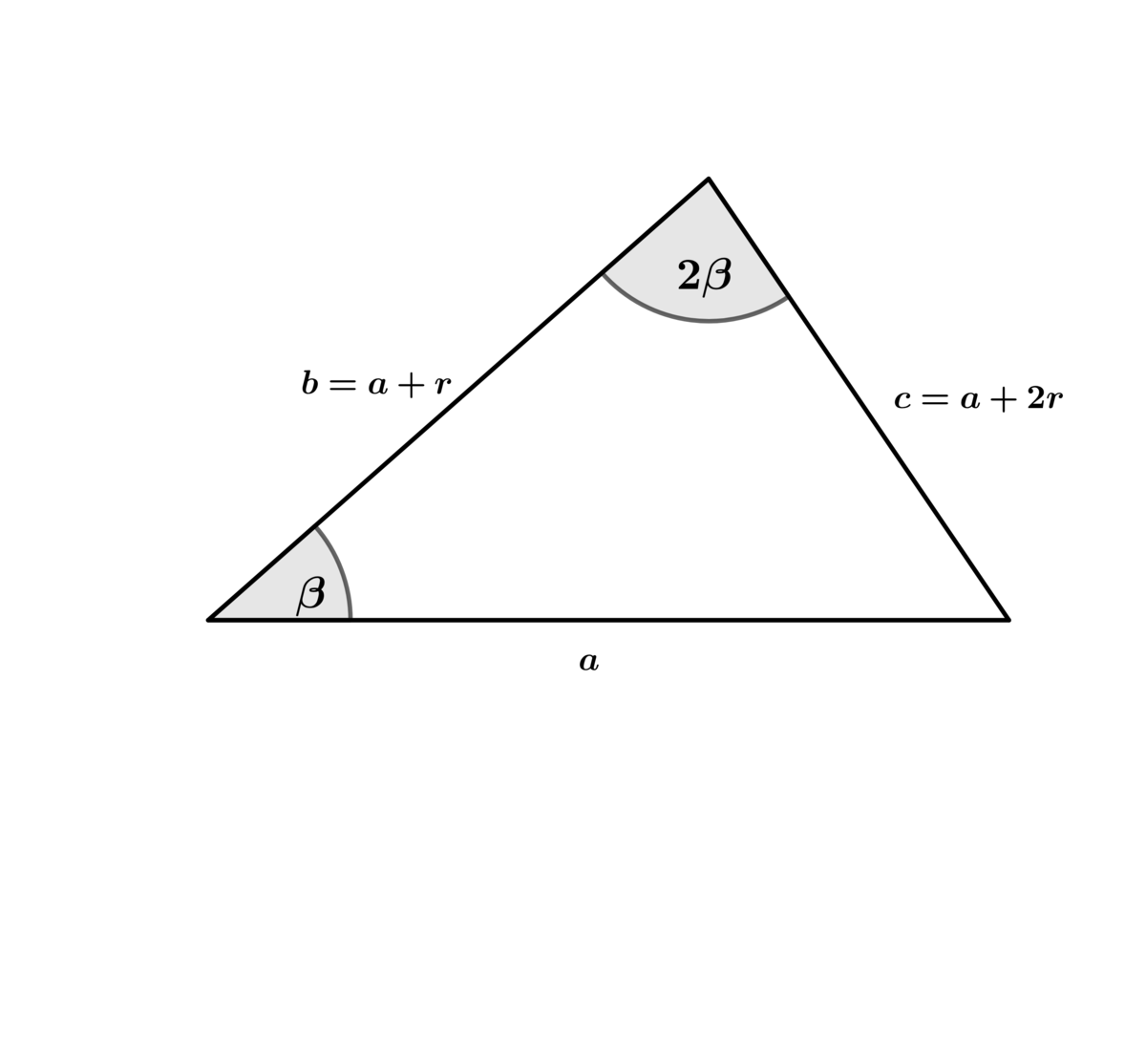
Using Law of Sines ⟹ sin ( β ) sin ( 2 β ) = a + 2 r a ⟹ cos ( β ) = 2 ( a + 2 r ) a
Using Law of cosines with included angle β ⟹ a 2 + 4 a r + 4 r 2 = a 2 + 2 a r + r 2 + a 2 − a + 2 r a 2 ( a + r ) ⟹ r ( 6 r 2 + 7 a r + a 2 ) = 0 r = 0 ⟹ r = − a , − 6 a r = − a ⟹ r = − 6 a ⟹ ( a , b , c ) = ( a , 6 5 a , 3 2 a )
⟹ a : b : c = 6 : 5 : 4 ⟹ a + b + c = 1 5 .
Read https://in.answers.yahoo.com/question/index?qid=20130801113139AA5kDrf
the proportion of the sides are: a : b : c = sin(A) : sin(B) : sin(C)
= 3√7/8 : 5√7/16 : √7/4 = 6 : 5 : 4
Answer: The sides of the triangle are in proportion as 6 : 5 : 4
By the sine law, sin 2 α a = sin α c , from which it follows that cos α = 2 c a (use the identity for sin 2 α ).
Because a , b , c form an arithmetic progression, b = 2 a + c , so now by the law of cosines:
c 2 = ( 2 a + c ) 2 + a 2 − 2 a ( 2 a + c ) ( 2 c a ) .
Simplify to get
3 c 3 = 3 a 2 c + 2 a c 2 − 2 a 3 .
If we now divide by c 3 and let c a = q , we obtain the equation:
2 q 3 − 3 q 2 − 2 q + 3 = 0
For which the solutions are 1 . 5 , 1 , − 1 . The only reasonable option is q = 1 . 5 , and so
a : b : c = 1 : 1 . 2 5 : 1 . 5 = 4 : 5 : 6
b= ( a+c ) /2 ,therefore a=2b-c ...✳︎ Let raise both side of this equation to the square, a^2=4b^2-4bc+c^2 ...① Then, if we define D for the intersection of BC and the bisector of angle A, we get DB = ac/( a+c ) follows from angle bisector theorem. Moreover, △ABC~△DBA, so c : a = ac/( b+c ) : c Therefore, c^2 = a^2c/( b+c ) c = a^2/( b+c ) ( divide both side by c) So, a^2 = bc+c^2 ...②
The equation 4b^2-4bc+c^2=bc+c^2 follows from ①,② So, 4b^2=5bc That is c = (4/5)b ...③ Let substitute ③ for ✳︎, a= 2b - (4/5)b = (6/5)b ...④ From ③,④ we get a : b: c = (4/5) : 1 : (6/5) = 4 : 5 : 6 So, a+b+c =4+5+6=15
a/sinA=b/sinB=c/sinC= 2R ——-(1). As the sides are in AP, 2b = (a + c)
Using (1), sin(B) = (sin(A) + sin(C))/2, we get:
sin(B) = sin{(A + C)/2}*cos{(A - C)/2} ----- (2)
By the given condition, taking angle C as the least, angle A as the greatest, ∠A=2∠C. So, A + C = 3C and A - C = C and ∠B=180−(∠A+∠C)=180−3C; so sin(B)=sin(180−3C)=sin(3C)
Substituting this in (2), sin(3C) = sin(3C/2)cos(C/2)
i.e. 2sin(3C/2)cos(3C/2) - sin(3C/2)cos(C/2) = 0
i.e. sin(3C/2){2cos(3C/2) - cos(C/2)} = 0
So either sin(3C/2) = 0 or 2cos(3C/2) - cos(C/2) = 0 If sin(3C/2) = 0, then C = 0, which is not possible; hence this is rejected.
So 2cos(3C/2) - cos(C/2) = 0 or {cos(3C/2)}/cos(C/2) = 1/2 {4cos³(C/2) - 3cos(C/2)}/cos(C/2) = 1/2
4cos²(C/2) - 3 = 1/2 cos²(C/2) = 7/8.. Hence cos(C/2) = √(7/8) only;
so sin(C/2) = √{1 - cos²(C/2)} = √(1/8)
so cos(C) = 2cos²(C/2) - 1 = 3/4
Substitute in the above, sin(C) = 2sin(C/2)cos(C/2) = 2{√(1/8)}{√(7/8)} = (√7)/4
sin(A) = sin(2C) = 2sin(C)cos(C) = 2{ (√7)/4)(3/4) = 3√7/8
sin(B) = sin(3C) = {3sin(C) - 4sin³(C)} = 3√7/4 - 4(√7/4)³ = 5√7/16
By sine rule, the proportions are a:b:c :: sin(A) : sin(B): sin(C) = 6 : 5 : 4.
Let a=b-d, b & c=b+d be the 3 sides, and A, B & C be the 3 angles. C =2 A. We know that sinC/c =sinA/a. This leads to sin(2A)/(b+d) = sinA/(b-d) . This gives 2sinAcosA= (b+d)/(b-d) sinA. This gives cosA = (b+d)/(2(b-d)). Also a^2 = b^2+c^2 -2.b.c.cosA. Substituting for a, c and cos (A) and simplifying we get b = 5d. Hence the sides are 4d, 5d and 6d. Hence the a+b+c =4+5+6=15
If d is the difference in the arithmetic progression of the sides, then b = c + d and a = c + 2 d , and if x is the smallest angle, then the biggest angle is 2 x and the third angle is 1 8 0 ° − 3 x .
Then by the law of sines, c sin x = c + d sin ( 1 8 0 ° − 3 x ) = c + 2 d sin 2 x .
Using trigonometric identities, sin 2 x = 2 sin x cos x = 2 sin x 1 − sin 2 x , and sin ( 1 8 0 ° − 3 x ) = sin 3 x = 3 sin x − 4 sin 3 x = sin x ( 3 − 4 sin 2 x ) . These can be substituted in the above law of sines equations for c sin x = c + d sin x ( 3 − 4 sin 2 x ) = c + 2 d 2 sin x 1 − sin 2 x , which solves to sin 2 x = 1 6 7 and d = 4 c .
Since a , b , and c are integers in an arithmetic progression, the difference d must also be an integer, and since d = 4 c , c must be divisible by 4 . Since a , b , and c are co-prime, c = 4 , which means d = 4 c = 4 4 = 1 , b = c + d = 4 + 1 = 5 and a = c + 2 d = 4 + 2 ⋅ 1 = 6 .
Therefore, a + b + c = 6 + 5 + 4 = 1 5 .