Find x x

Geometry Level 3


The answer is 12.7017.

Aly Ahmed by Aly Ahmed , 34, Egypt

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

4 solutions

7 Helpful 5 Interesting 9 Brilliant 0 Confused

can u help.. https://brilliant.org/discussions/thread/how-to-approach-this-question/

Syed Hamza Khalid - 1 year, 4 months ago

Log in to reply

you are asking me?

nibedan mukherjee - 1 year, 4 months ago

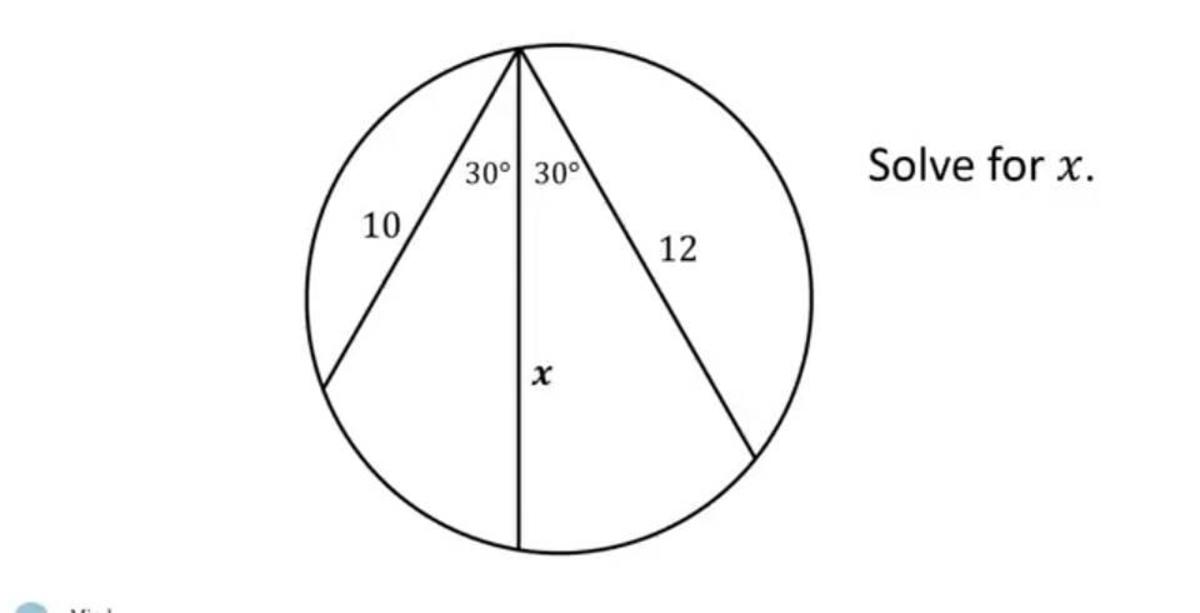
Let the radius of the circle be r r . Then cos ⁡ 30 ° = √ 3 2 = 100 + x 2 − r 2 20 x = 144 + x 2 − r 2 24 x \cos {30\degree}=\dfrac{√3}{2}=\dfrac{100+x^2-r^2}{20x}=\dfrac{144+x^2-r^2}{24x} . Or 2 √ 3 x = 44 2√3x=44 or x = 22 √ 3 = 12.7017... x=\dfrac{22}{√3}=\boxed {12.7017...}

1 Helpful 2 Interesting 7 Brilliant 3 Confused

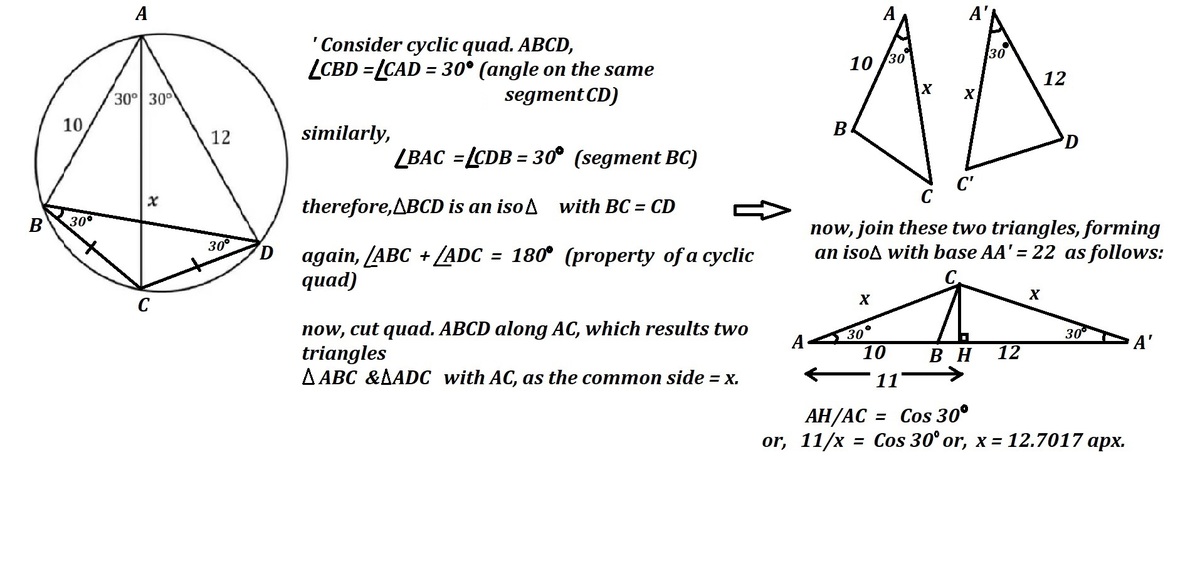
Refer to the diagram of Chew-Seong Cheong. Let O be the centre of the circle. Note that / DOC=60°. Also / BOC=60° which make Tr. DOC & Tr. BOC equilateral and hence DC=BC=r. Then it follows from Tr. ADC that: √3/2 = ​(100+x²-r²)/(20x). Likewise, from Tr. ABC: √3/2 = ​(144+x²-r²)/(24x). Solve the two equations to get x=22/√3. Nice solution Alak Bhattacharya.

ajit athle - 1 year, 4 months ago

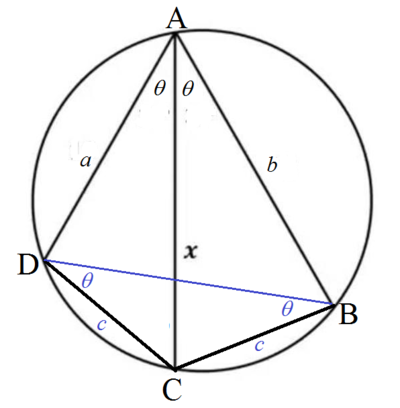
Providing a general solution as suggested by @Nikola Alfredi . Therefore, instead of 10 10 , 12 12 , and 3 0 ∘ 30^\circ , we have a a , b b , and θ \theta respectively.

Since A B C D ABCD is a cyclic quadrilateral , then ∠ B A C = ∠ B D C = θ \angle BAC = \angle BDC = \theta and ∠ C A D = ∠ C B D = θ \angle CAD = \angle CBD = \theta . Then △ B C D \triangle BCD is isosceles and B C = C D = c BC=CD = c . By Ptolemy's theorem , we have:

A C ⋅ B D = A D ⋅ B C + A B ⋅ D C Let B D = y x y = a c + b c Note that y = 2 c cos ⁡ θ ⟹ x = a c + b c 2 c cos ⁡ θ = a + b 2 cos ⁡ θ \begin{aligned} AC \cdot \blue{BD} & = AD \cdot BC + AB \cdot DC & \small \blue{\text{Let }BD=y} \\ x\blue y & = ac+bc & \small \blue{\text{Note that }y = 2c\cos \theta} \\ \implies x & = \frac {ac+bc}{2c\cos \theta} = \frac {a+b}{2\cos \theta} \end{aligned}

For a = 10 a=10 , b = 12 b=12 , and θ = 3 0 ∘ \theta = 30^\circ , x = 22 3 ≈ 12.702 x = \dfrac {22}{\sqrt 3} \approx \boxed{12.702} .

2 Helpful 2 Interesting 3 Brilliant 0 Confused

General Formula for such type of questions where

a ≠ b T h e n x = a + b 2 cos ⁡ θ \ \ \displaystyle a \neq b \ \ \ Then \ \ \ x = \frac {a + b}{2 \cos \theta}

Nikola Alfredi - 1 year, 4 months ago

Log in to reply

Thanks for your suggestion. I have provided the general solution.

Chew-Seong Cheong - 1 year, 4 months ago

Log in to reply

You're welcome

Nikola Alfredi - 1 year, 4 months ago

@Nikola Alfredi ,Suppose the angle between a and b are different, Then what would be your answer? Is it a + b cos ⁡ α + cos ⁡ β ? \frac{a+b}{\cos{\alpha}+\cos{\beta}}?

Winod DHAMNEKAR - 1 year, 4 months ago

Log in to reply

@Winod DHAMNEKAR

I will tell you soon but I belief that the question will be incomplete with the given data. It must require at least one more value point...

Nikola Alfredi - 1 year, 4 months ago

@Winod DHAMNEKAR

Hi, As I said there would be no question like this but if it exists then solution would be :

Assume ∠ B A C = β \angle BAC = \beta and ∠ D A C = α \ \angle DAC = \alpha

Solution : (A polynomial)

2 x 4 cos ⁡ ( α + β ) − 4 x 3 ( a cos ⁡ α + b cos ⁡ β ) ( cos ⁡ ( α + β ) ) + 2 x 2 [ ( a 2 + b 2 + 4 a b cos ⁡ α cos ⁡ β ) ( cos ⁡ ( α + β ) ) + 1 ] + 2 x [ 2 a b ( b cos ⁡ α + a cos ⁡ β ) cos ⁡ ( α + β ) − ( a cos ⁡ α + b cos ⁡ β ) ] + 2 a b cos ⁡ ( α + β ) + a 2 b 2 = 0 \displaystyle 2x^4 \cos(\alpha + \beta) - 4x^3 (a \cos \alpha + b \cos \beta)(\cos(\alpha + \beta)) + 2x^2[(a^2 +b^2 + 4ab \cos \alpha \cos \beta)(\cos(\alpha + \beta)) + 1] +2x[2ab(b \cos \alpha + a \cos \beta) \cos(\alpha + \beta) - (a \cos \alpha + b \cos \beta)] + 2ab \cos(\alpha + \beta) + a^2b^2 = 0

Nikola Alfredi - 1 year, 4 months ago

Log in to reply

This equation don't give answer for the case a = 10 , b = 12 , α = β = 30 ° a = 10\,,\, b = 12\,,\, \alpha = \beta = 30\degree For this case this equation has no solution.

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

x 2 = a 2 + b 2 − 2 a b cos ( α + β ) sin 2 ( α + β ) cos 2 ( θ − β ) \large x^2 = \Large \frac{a^2 + b^2 -2ab\text{cos}(\alpha + \beta)}{\text{sin}^2(\alpha + \beta)} \text{cos}^2(\theta - \beta) where

cos 2 ( θ ) = b 2 sin 2 ( α + β ) a 2 + b 2 − 2 a b cos ( α + β ) \Large \text{cos}^2(\theta) = \frac{b^2\text{sin}^2(\alpha + \beta)}{a^2 + b^2 -2ab \text{cos}(\alpha + \beta)}

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

@Shikhar Srivastava – Ok, thank you

Nikola Alfredi - 1 year, 4 months ago

@Shikhar Srivastava – @Shikhar Srivastava I found the formula just by using Cosine-Rule in Δ B A C & Δ D A C & Δ B C D \Delta BAC \ \& \ \Delta DAC \ \& \ \Delta BCD why does it goes wrong any clue....?

Nikola Alfredi - 1 year, 4 months ago

@Shikhar Srivastava – How did you find it ... just give hint.

Nikola Alfredi - 1 year, 4 months ago

Log in to reply

@Nikola Alfredi – Let O O be the center of the circle. First find the radius of circle. Suppose ∠ A B O = θ . \angle ABO = \theta . Then find expression for θ \theta . Then find ∠ A O C \angle AOC in terms of θ \theta and β \beta . After this in △ A O C , A O , O C , ∠ A O C \triangle AOC\,,\, AO , OC \,,\, \angle AOC is known. you can find A C AC

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

@Shikhar Srivastava – @Shikhar Srivastava Thank you very much for the help. But did you found why error is coming in my equation......

Nikola Alfredi - 1 year, 4 months ago

Log in to reply

@Nikola Alfredi – What you are doing ? By applying cosine rule what sides or angle are you finding and in which sequence ? Please tell me so that I may help you.

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

@Shikhar Srivastava – Ok, First I used Cosine rule in Δ A B C \Delta ABC and found B C 2 BC^2 then I Found C D 2 CD^2 , Similarly I found B D 2 BD^2 by Cosine rule and then finally in Δ B C D \Delta BCD I used the Cosine rule.... This is all I did..

I tried your way and I believe it's cool and easy....

Nikola Alfredi - 1 year, 4 months ago

@Shikhar Srivastava – Hey, I got it :)

Nikola Alfredi - 1 year, 4 months ago

@Shikhar Srivastava I think your formula for x 2 x^2 requires some corrections. Put a = 10 , b = 5 , α = 38. 9 ∘ a n d β = 77.2 1 ∘ a=10, b=5,\alpha=38.9^\circ and \beta=77.21^\circ .

Example Link

Winod DHAMNEKAR - 1 year, 4 months ago

Log in to reply

In your link angles α \alpha and β \beta are not taking the entries. Only sides and diagonals are allowed to fill. On putting the values as you said the value is coming x = 14.417 x = 14.417 . Is it not correct ? Please tell me the exact problem so that I will look into it.

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

In the link, put a=9, b=10,c=5, d=14, diagonal AC=13. You will get β 1 = 38. 9 ∘ , β 2 = 77.2 1 ∘ \beta_1=38.9^\circ, \beta_2=77.21^\circ . You will get diagonal BD(which is x in our case, we want to find out)=14.23. Comparing it to your answer 14.417 ,it is approximately same not exact.

Winod DHAMNEKAR - 1 year, 4 months ago

Log in to reply

@Winod Dhamnekar – The quadrilateral A B C D ABCD in your case is not cyclic.

Shikhar Srivastava - 1 year, 4 months ago

Log in to reply

@Shikhar Srivastava – @Shikhar Srivastava , It is a cyclic quadrilateral. d 1 d 2 = a c + b d , 13 ∗ 14.23 = 9 ∗ 5 + 10 ∗ 14 , ⇒ 184.99 = 185 d_1d_2=ac+bd, 13*14.23=9*5+10*14, \Rightarrow 184.99=185 with only 0.01 absolute error.

Winod DHAMNEKAR - 1 year, 4 months ago

Log in to reply

@Winod Dhamnekar – cos ( B ) = A B 2 + B C 2 − A C 2 2 ⋅ A B ⋅ B C = 100 + 25 − 169 2 ⋅ 10 ⋅ 5 = − 44 100 = − 11 25 \text{cos}(B) = \large\frac{AB^2 + BC^2 - AC^2}{2\cdot AB\cdot BC} = \frac{100 + 25 - 169}{2\cdot 10\cdot 5} = \frac{-44}{100} = \frac{-11}{25}

cos ( D ) = A D 2 + D C 2 − A C 2 2 ⋅ A D ⋅ D C = 81 + 196 − 169 2 ⋅ 9 ⋅ 14 = 108 252 = 3 7 . \text{cos}(D) = \large\frac{AD^2 + DC^2 - AC^2}{2\cdot AD\cdot DC} = \frac{81 + 196 - 169}{2\cdot 9\cdot 14} = \frac{108}{252} = \frac{3}{7}.

For cyclicity of quadrilateral, ∠ B + ∠ D = 180 ° ⇒ ∠ B = 180 ° − ∠ D ⇒ = cos ( B ) = cos ( 180 ° − D ) = − cos ( D ) \angle B + \angle D = 180\degree \Rightarrow \angle B = 180\degree - \angle D \Rightarrow = \text{cos}(B) = \text{cos}(180\degree - D) = -\text{cos}(D) which is not in your case. Hence not cyclic.

Shikhar Srivastava - 1 year, 4 months ago

I got the mistake. The mistake is I forgot to square the term cos ( θ − β ) \text{cos}(\theta - \beta) in the expression of x 2 x^2 . Actually it should be cos 2 ( θ − β ) \text{cos}^2(\theta - \beta) I have corrected it.

Shikhar Srivastava - 1 year, 4 months ago
Vinod Kumar
May 2, 2020

Using property of cyclic quadrilateral, opposite angle sum is 180 degree. Solve 12 sin(x)=10 sin(2 pi/3-x), y=sin(x), z=sin(150-x). Then w=10 z/y =12.7017 is the answer.

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...