Find the Zeros
One real zero of f ( x ) = x 3 − ( p − 2 ) x 2 + ( − p − 1 1 ) x + 1 2 p − 1 2 is x = p − 1 . Find the other two real zeros.
Enter your answer as a 2 + b 2 , where a and b are the other two real zero solutions.
The answer is 25.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
I hadn't thought about this method. Nicely done!
Wow that's smart
We can also proceed by not finding out the zeroes. Instead we can use Vieta's formula and manipulate a^2+b^2 to find it's value......It's shorter and doesn't need synthetic division...
This looks like a great approach! Can you provide some more details on how you used Vieta's formula to arrive at the answer?
Log in to reply
Well.....I dont know Latex so.......a^2+b^2=(a+b)^2-2ab.........Now, a+b+(p-1)=p-2......so, a+b=-1.........similiarly, a b (p-1)=-12(p-1).............so, ab=-12..........putting these values gives us the desired answer......Hope it helps!!
Log in to reply
Nicely done!
Using synthetic division , we see that x 3 − ( p − 2 ) x 2 + ( − p − 1 1 ) x + 1 2 p − 1 2 = ( x − ( p − 1 ) ) ( x 2 + x − 1 2 ) (see below).
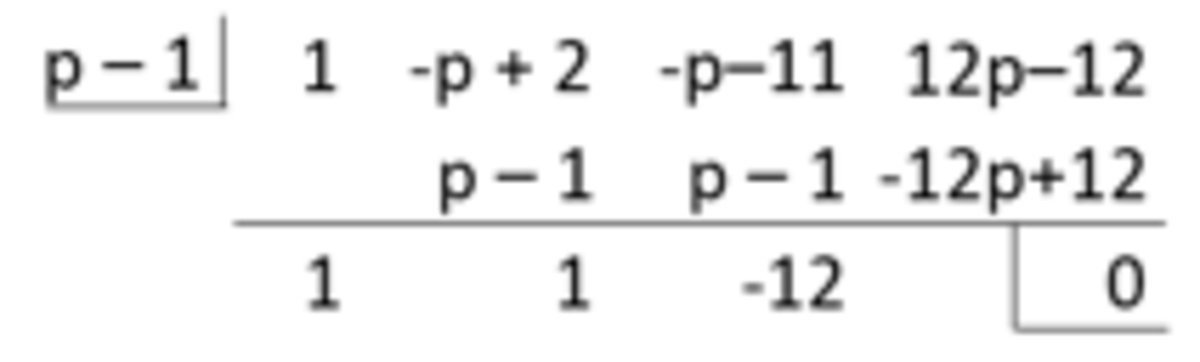
x 2 + x − 1 2 can be further factored to ( x − 3 ) ( x + 4 ) , so the two other real zeros are a = 3 and b = − 4 , and 3 2 + ( − 4 ) 2 = 2 5 .
Since f ( p − 1 ) simplifies to 0, this means that p can be any number.
For simplicity, let p = 1 , then f ( x ) = x 3 + x 2 − 1 2 x = x ( x 2 + x − 1 2 ) = x ( x + 4 ) ( x − 3 ) has roots ( p − 1 = 0 ) , − 4 , 3 .
The answer is ( − 4 ) 2 + 3 2 = 2 5 .