This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
In the second-to-last step, how did you choose 1 5 0 ∘ instead of 3 0 ∘ to use as arcsin ( 2 1 ) ?
Log in to reply
You are right I should choose both.
Log in to reply
Is there a reason why 6 ∘ is the answer and not 6 8 ∘ ?
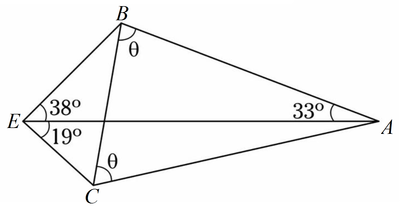
Let ∠ A B C = ∠ A C B = θ . Then ∣ B C ∣ = 2 ∣ A B ∣ cos θ . Let ∠ A E B = 3 8 ° , ∠ B A E = 3 3 ° , ∠ A E C = 1 9 ° . Then ∣ A E ∣ ∣ A B ∣ = sin 1 0 9 ° sin 3 8 ° = 2 sin 1 9 ° , ∣ A E ∣ ∣ A C ∣ = sin ( 1 4 ° + 2 θ ) sin 1 9 ° . ∣ A B ∣ = ∣ A C ∣ ⟹ sin ( 1 4 ° + 2 θ ) = 2 1 . So θ can be 8 ° or 6 8 ° .
@Alak Bhattacharya , I have provided a diagram for you.
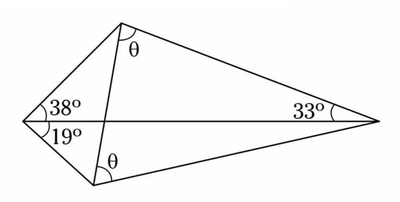
Note that △ A B C is isosceles that is A B = A C . We have ∠ E B A = 1 8 0 ∘ − 3 8 ∘ − 3 3 ∘ = 1 0 9 ∘ , ∠ E A C = 1 8 0 ∘ − 2 θ − 3 3 ∘ and ∠ E C A = 1 8 0 ∘ − ( 1 8 0 ∘ − 2 θ − 3 3 ∘ ) − 1 9 ∘ = 2 θ + 1 4 ∘ . By sine rule ,
⎩ ⎪ ⎨ ⎪ ⎧ A B E A = sin 3 8 ∘ sin 1 0 9 ∘ A C E A = sin 1 9 ∘ sin ( 2 θ + 1 4 ∘ ) . . . ( 1 ) . . . ( 2 )
Since A B = A C ,
sin 1 9 ∘ sin ( 2 θ + 1 4 ∘ ) sin ( 2 θ + 1 4 ∘ ) sin ( 2 θ + 1 4 ∘ ) ⟹ 2 θ + 1 4 θ = sin 3 8 ∘ sin 1 0 9 ∘ = 2 cos 1 9 ∘ sin 7 1 ∘ = 2 cos 1 9 ∘ cos 1 9 ∘ = 2 1 = 3 0 ∘ or 1 5 0 ∘ = 6 ∘ or 6 8 ∘ Note that sin ( 1 8 0 ∘ − ϕ ) = sin ϕ and sin ( 2 ϕ ) = 2 sin ϕ cos ϕ also sin ϕ = cos ( 9 0 ∘ − ϕ )