Find velocity after $2{ C}$ seconds?

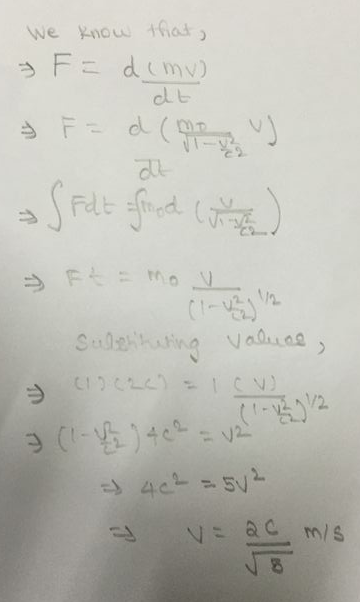
Let's start from the equation

$\frac{dp}{dt}=F$

where p is the momentum of a particle experiencing a force F. If the force is constant, and the initial momentum is zero, this is easily integrated to give

$p=Ft$

We now substitute the relativistic form for the momentum to get

$\frac{mu}{\sqrt{1-\frac{u^2}{c^2}}}=Ft$

It is not too hard to solve this for the speed u by first squaring both sides and solving for $u^2$ . Then

$u=Ft\sqrt{\frac{1}{m^2+\frac{F^2t^2}{c^2}}}\dots*$

Finally substitute in the values for this problem to get

$u=2c\sqrt{\frac{1}{1+\frac{4c^2}{c^2}}}=\frac{2c}{\sqrt{5}}$

*NOTE. The second term in the denominator of this equation contributes the relativistic effects. It becomes significant for large values of t, when the force has been acting long enough to produce relativistic velocities. If you let t tend to infinity in * the second term dominates the denominator and $u \rightarrow c$ , consistent with c being a universal speed limit. On the other hand for small values of t the second term can be neglected and * reduces to the Newtonian solution $u=\frac{Ft}{m}$

Correct me if I am Wrong.