Radical sum
If x is a real number satisfying the equation x + 1 5 + x = 1 5 , find the value of x .
The answer is 49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
45 solutions
why 30 on right side??
Log in to reply
Note that ( a − x ) 2 = a 2 − 2 a x + x , a = 1 5 ⟹ 2 a = 3 0 .
Log in to reply
should that be ......... = a squared - 2a multiplied by sqrt x
minus
x ?
That's the only way i can get it to work.
Log in to reply
@Gareth Clark – No, ( a − x ) 2 = a 2 − 2 a x + ( − x ) 2 = a 2 − 2 a x + x
Log in to reply
@Chew-Seong Cheong – ok, I see. Thanks for that.
Square both sides give two -15 sqrt(x), combine to -30 sqrt(x), then normalize to make both sides positive.
This one seems the simplest way to solve, Chew-Seong's solution....
Much simpler ..
15=8+7 and 6+9 and 5+10 and 4+11 Sqroot(x+15)=11 and Sqroot (x) = 4 ? => No X ! Sqroot(x+15)=10 and Sqroot (x) = 5 => No X ! Sqroot(x+15)=9 and Sqroot (x) = 6 ? => No X ! Sqroot(x+15)=8 and Sqroot (x) = 7 ? => X=49 !
Yippiiii ..
Log in to reply
This is only valid if we assume that x is an integer.
Did exactly like this. :)
Pfff, easy
I just got it by iteration cuz the numbers are very simple.. the second iteration 8|
why can't x be 0. That will be the simplest solution
Log in to reply
Then, it will be 1 5 = 1 5 .
That is the answer I got....zero.
sqrt(15) is not equal to 15.
By difference of squares , we know that ( a − b ) ( a + b ) = a 2 − b 2 .
In this case, let a = x + 1 5 , b = x . We have
( x + 1 5 − x ) ( x + 1 5 + x ) ( x + 1 5 − x ) ⋅ 1 5 x + 1 5 − x = = = ( x + 1 5 ) − x 1 5 1 .
Adding this equation to the original equation given shows
( x + 1 5 − x ) + ( x + 1 5 + x ) 2 x + 1 5 x + 1 5 x + 1 5 x = = = = = 1 5 + 1 1 6 8 6 4 4 9 .
I done by using intellectual method, the only square numbers with difference 15 are 49 and 64 .Therefore,√x=7 and √x+15=8.7+8=15.
Log in to reply
(Ignoring that Brilliant tells you the answer has to be an integer) Why must these be perfect squares? What's so special about the number 15?
For example, note that 4 1 would be the solution to x + 2 + x = 2 .
Great solution! +1
Log in to reply
:)
I like these solutions (and problems) which make use of ideas from other areas to simplify what is going on. When I see them, I try and share them.
( x + 1 5 + x ) 2 = 1 5 2
x + 1 5 + 2 x 2 + 1 5 x + x = 2 2 5
2 x 2 + 1 5 x = 2 1 0 − 2 x
x 2 + 1 5 x = 1 0 5 − x
( x 2 + 1 5 x ) 2 = ( 1 0 5 − x ) 2
x 2 + 1 5 x = 1 0 5 2 − 2 1 0 x + x 2
2 2 5 x = 1 1 0 2 5
x = 4 9
This is just wrong. So much longer.
Log in to reply
Who are you to tell me this is wrong? Although longer than the other, more concise solutions, this is still a valid solution and valid approach to solving for x .
first time post: sequential squares of natural numbers increase by 2n+1. i just subtracted 1 from 15 and divided by 2 to get root x. root x =7 so x =49. these posts are hard to do on a phone
nice observation >>>
I didn't get it, I see that works, but don't know why.
Log in to reply
Assuming the results of the radicals must be natural numbers in order to add up to 15, you must pick a value for x that has a natural root, and for which that value of x plus 15 has a natural root. The sequence of squares proceeds in a very orderly fashion: 1, 4 or (1 + 3), 9 or (4 + 5), 16 or (9 + 7), 25 or (16 + 9), 36 or (25 + 11), 49 or (36 + 13), 64 or (49 + 15)! (Note how the second term in each parentheses is an ever increasing odd number, or 2n + 1). And there it is, the value for x is 49 providing the natural root of 7, and then 49 plus 15 equals 64 providing the natural root of 8, 7 plus 8 satisfies 15. Does that explain it?
⟹ ⟹ ⟹ ⟹ x + 1 5 + x ( x + 1 5 ) 2 x + 1 5 x x = = = = = 1 5 ( 1 5 − x ) 2 2 2 5 + x − 3 0 x 7 4 9
Great job keeping the implication signs around.
Always be careful when you square both sides of the equation, you run the risk of introducing extraneous roots. So, what you have is a necessary condition, but it may not be sufficient.
IE Your implication signs only work one way, and so we still have to verify that x = 4 9 does satisfy the original equation.
Log in to reply
Thanks. I believe that I understand your point. You mean that when I am squaring both sides of the equation, I can introduce more roots like this:
For simple linear equation x − 7 = 2 if I purposely square both sides, I get x 2 + 4 9 − 1 4 x = 4 x 2 − 1 4 x + 4 5 = 0 x = 9 or 5
Where x = 5 isn't clearly a root for the original equation above.
The coefficient of x term in both the radicals was 1 in this problem. Is that the reason why I didn't arrive at a situation as stated above in my example?
No, he doesn't have to verify that x=49 satisfy the original equation. Becuse Square root is always positive. Then if he square both sides of the equation, they are still positive.
Log in to reply
Suppose that the equation was instead x + 1 5 − x = − 1 5 . We can similarly move the term over and square them to get ( x + 1 5 ) 2 = ( − 1 5 + x ) 2 . Does this then imply that x = 4 9 must be a solution to the original equation? Unfortunately no, because when we square the equation, we are "forgetting" the sign before the terms. What we have is just ∣ x + 1 5 ∣ = ∣ − 1 5 + x ∣ , meaning that these values are the same up to a change of sign.
This example shows why it's important to check the square roots, Yes, you might claim "But we know right from the start that there are no solutions to the equation", but my intention was to keep close to the spirit of this problem. You can create similar scenarios where the squaring results in introducing solutions to the problem, when there were originally none.
x + 1 5 + x = 1 5
If x ∈ R , then x ≥ 0
After squaring both sides and simplifying:
2 x + 1 5 + 2 x ( x + 1 5 ) = 2 2 5
2 x ( x + 1 5 ) = 2 1 0 − 2 x
x 2 + 1 5 x = 1 0 5 − x
After squaring again:
x 2 + 1 5 x = x 2 − 2 1 0 x + 1 1 0 2 5
2 2 5 x = 1 1 0 2 5
x = 4 9
Indeed:
4 9 + 1 5 + 4 9 = 1 5
8 + 7 = 1 5
Here's a simple solution. Since 15 is a whole number, we expect Sqrt(x) to at least be a rational number. It has to be the case that the square root of x is smaller than half of 15. First we assume that sqrt(x) is an integer, and so is sqrt(x+15). This requires both x and x+15 to be square numbers. By inspection, we can see that these conditions only hold for 49 and 64. If the square root of x is 7, then this becomes Sqrt(64) + Sqrt(49) = 8 + 7 = 15, as desired.
Yes. This is how I solved it. Required no algebra at all. Took roughly a second to see that the two squares separated by 15 must be 49 and 64.
Let a = x + 1 5 and b = x . So, a 2 − b 2 = x + 1 5 − x = 1 5 and a + b = 1 5 , a − b = a + b a 2 − b 2 = 1 5 1 5 = 1 and a + b = 1 5 , 2 b = ( a + b ) − ( a − b ) = 1 5 − 1 = 1 4 , b = 7 , x = b 2 = 7 2 = 4 9 .
This can be solved in a simple manner if one remembers the following
"n^2 = Sum of first n odd numbers"
ie.
1^2 = 1
2^2 = 1+3 = 1^2+3
3^2 = 1+3+5 = 2^2+5
and so on.
Here it is highly likely that √(x+15) and √x are both integers
15 is the 8th odd number and for (x+15) and x to be perfect squares x has to be the sum of first 7 odd numbers ie 7^2 = 49.
Just to be different.
x + 1 5 + x = 1 5
Multiply by 15.
1 5 x + 1 5 + 1 5 x = 2 2 5
Subtract 15.
1 5 x + 1 5 x = 2 1 0
Simplify.
3 0 x = 2 1 0
Divide by 30.
x = 7
Square.
x = 4 9
Consider a right trangle, whose sides are A = x , B = 1 5 , C = x + 1 5 . Then, the given equation is
A + C = B 2 (1)
But also, B 2 = C 2 − A 2 , from Pythagoras Theorem. Then,
A + C = B 2 = C 2 − A 2 = ( C + A ) ( C − A ) , thereby,
C − A = 1 (2)
Therefore, substracting (2) from (1), one has that
( A + C = 1 5 ) − ( C − A = 1 ) = 2 A = 1 4
Hence A = 7 , but A = x , whence,
x
=
4
9
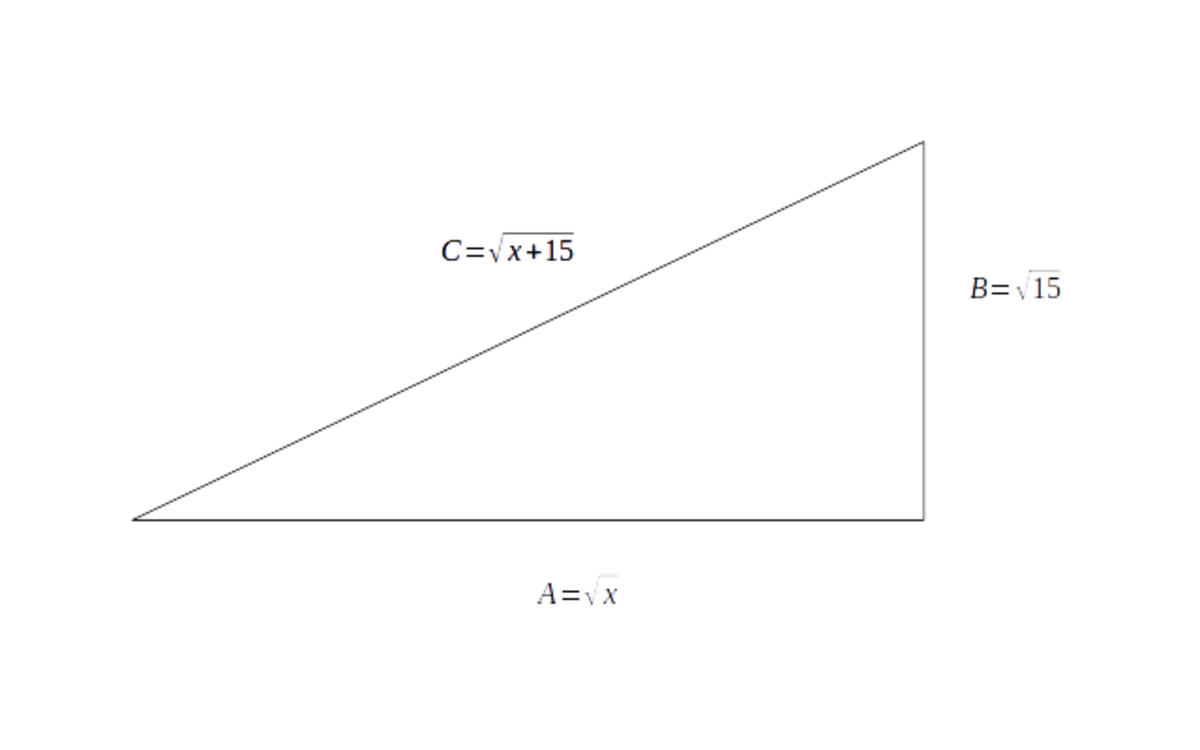
None of the top answers took the slightly easier route. I don't know how to write solutions so they look pretty, but who cares...
Move the sqrt x to the other side
sqrt(x + 15) = 15 - sqrt(x)
Square both sides:
x + 15 = 225 - 30sqrt(x) + x
Cancel x, subtract 225 from both sides, divide by -30:
sqrt(x) = 7, x = 49
BOOM, NICE
Hey! I did it in a similar way. I can teach you LATEX, if you want. And it would give your solution the desired effect --- make it look really captivating! See my solution on this problem also.
( x + 1 5 − x ) ( x + 1 5 + x ) = 1 5 ( x + 1 5 − x )
1 5 = 1 5 ( x + 1 5 − x )
x + 1 5 − x = 1
taking the difference beetween the text and this equivalent equation we get:
2 x = 1 4
7 = x
First reasoning: I suppose x + 1 5 and x are perfect square. So m 2 − n 2 = 1 5 and ( m − n ) ( m + n ) = 3 ⋅ 5 so that m=4 and n=1 but this couple does'nt solve the equation, otherwise ( m − n ) ( m + n ) = 1 5 ⋅ 1 and we get m=8, n=7 and this couple is right. So that x = n 2 = 4 9 . And I was lucky when I supposed x could be an Integer.
You can solve this by simply plugging-in. Sum of square root of two numbers have to be 15. One is that number and another is the number + 15. That reduces the possible candidates to 64 and 49 from a list of whole squares candidates ( 1,4,9,16,25,36..). So x has to be 49
From the above equation it can be said that 15 is the summation of two full number square integer whose difference is 15 .
now let's just find out the square numbers
1²=1;
2²=4; difference=3.
3²=9; difference=5.
4²=16; difference=7.
5²=25; difference=9.
6²=36; difference=11.
7²=49; difference=13.
8²=64; difference=15.
So the answer should be 49. (no mathematical calculation is needed.)
x + 1 5 + x = 1 5
Solution
x = 1 5 − x + 1 5
Square both sides, expand, and simplify ...
( x ) 2 = ( 1 5 − x + 1 5 ) 2
x = ( 1 5 ) 2 − 2 ⋅ 1 5 ⋅ x + 1 5 + ( x + 1 5 ) 2
x = 2 2 5 − 3 0 x + 1 5 + x + 1 5
Try to isolate x ...
3 0 x + 1 5 = 2 2 5 + 1 5
3 0 x + 1 5 = 2 4 0
x + 1 5 = 3 0 2 4 0
Again square both sides to get rid of the unwanted root ...
x + 1 5 = 8 2
And you end up with ...
x = 6 4 − 1 5
∴ x = 4 9
Proof
Plug in the value and you get...
4 9 + 1 5 + 4 9
which yields...
8 + 7 = 1 5 .
Always be careful when you square both sides of the equation, you run the risk of introducing extraneous roots. So, what you have is a necessary condition, but it may not be sufficient. IE We still have to verify that x = 4 9 does satisfy the original equation.
Log in to reply
@Calvin Lin Thanks a bunch for the advice! I've edited the solution.
F i n d i n g a g e n e r a l s o l u t i o n , l e t 1 5 = y y = x + y + x ( 1 ) s q u a r i n g b o t h s i d e s y 2 = y + 2 x + 2 x ( x + y ) y 2 = y + 2 x ( x + x + y ) f r o m ( 1 ) y 2 = y + 2 x ( y ) ( y − 1 ) [ y − ( 1 + 2 x ) ] = 0 y = 1 a s y = 1 5 t h i s e q u a t i o n i s u s e l e s s . t h e r e f o r e y − ( 1 + 2 x ) = 0 x = 2 y − 1 x = ( 2 y − 1 ) 2 a t y = 1 5 , x = 4 9
x + 1 5 + x = 1 5
Subtract x from both sides, we obtain
x + 1 5 = 1 5 − x
Square both sides of the equation,
( x + 1 5 ) 2 = ( 1 5 − x ) 2
x + 1 5 = 1 5 2 − 3 0 x + x , from here x and x cancels out
1 5 + 2 2 5 − 3 0 x
Simplifying further, we have
3 0 x = 2 1 0
Divide both sides by 3 0 then square both sides,
x = 4 9
Do you know that this question is used on an advert for Brilliant?
Even x is a real number. We could expect that x and x + 1 5 are positive integers for the first try.
Since 2 x < x + 1 5 + x = 1 5 , we have x < 7 . 5 .
A quick test with x = 7 give us the correct answer.
Mathematica
NSolve[Sqrt[x + 15] + Sqrt[x] == 15, x]
{{x -> 49.}}
Do it mentally.
Try using the square numbers, obviously the ones greater than 15. for eg- * 25, 36,49,64,81 * Remember, your x has to be a square number, to be get easily rooted, and so does (x+15). Now choose a square number from the list, that when you add 15 to it gives you another square number. For eg: 49+15= 64, now replace (x+15) with 64 and x with 49. √64 + √49 = 15
We can see that both x+15 and x has to be perfect squares. Now in 2 or 3 hit and trials we know the answer is 49. there are straight methods for everything but i believe in some cases tricks might save time and solving equations.
x + 1 5 + x = 1 5 ( 1 )
x + 1 5 − x ( x + 1 5 + x ) ( x + 1 5 − x ) = 1 5
x + 1 5 − x 1 5 = 1 5
x + 1 5 − x = 1 ( 2 )
( 1 ) − ( 2 ) : 2 x = 1 4
x = 7
x = 4 9
√x+15 + √x = 15
√x+15 = 15 - √x
(√x+15 = 15 - √x)^2
x + 15 = (15-√)(15-√x)
x + 15 = 225 - 15√x - 15√x + x
-30√x = 210
√x = -7
x = 49
(\sqrt{x+15}+\sqrt{x})^{2}=15^{2} x+15+2\sqrt{(x+15)*x}+15=225 2\sqrt{(x^{2}+15x}=225-15-2x (2\sqrt{(x^{2}+15x})^{2}=(210-2x)^{2} 4(x^{2}+15x)=44100-840x+4x^{2} 900x=44100 x=\frac{44100}{900} x=49
Here x must be moderately large. The square roots of x + 15 and x must be very similar. e.g. 8 and 7. Try x = 49. No need for any complicated maths here!
x=a^2, a^2+15=(a+1)^2
so a =7, x=49.
Premise: The solution is easy. That means that both x and x + 1 5 are integers. Probably consecutive. As everyone knows ( n + 1 ) 2 − n 2 = 2 n + 1 , therefore if 2 n + 1 = 1 5 , then n = 7 . Indeed 7 + 8 = 1 5 ; this leads to a solution x = n 2 = 4 9 . By a mental manipulation of the identity, and squaring, one can observe that it has a unique solution.
By conjugation method , without any squaring both side.
x + 1 5 + x = 1 5
x + 1 5 − x = 1
Subtract both equation
2 x = 1 4 x = 7 x = 4 9
x + 1 5 + x = 1 5
( x + 1 5 + x ) ( x + 1 5 − x x + 1 5 − x ) = 15 <- multiply Left Hand Side with its conjugate
x + 1 5 − x ( x + 1 5 ) − ( x ) = 1 5
x + 1 5 − x 1 5 = 1 5
x + 1 5 − x 1 = 1
x + 1 5 − x = 1
By conjugation method , without any squaring both side.
I still see squaring. But I'm just being unnecessarily picky with your wording.
x = 7 x = 4 9
simplify the equation by transferring one radical at the right side of the equation. then square both sides. then simplify again and then use the quadratic equation in getting the value of x. x=49
Reason: √(x+15)=15-√x Now, square both sides of the equation X+15=225-30√x+x 15=225-30√x 30√x=210 √x=7, Therefore, x=49
( x + 1 5 ) + ( x ) = 1 5
we need to find 2 squares, whose square roots add up to 15, 15 apart
| 0 | 0 | 15 | 225 |
| 1 | 1 | 14 | 196 |
| 2 | 4 | 13 | 169 |
| 3 | 9 | 12 | 144 |
| 4 | 16 | 11 | 121 |
| 5 | 25 | 10 | 100 |
| 6 | 36 | 9 | 81 |
| 7 | 49 | 8 | 64 |
we find 49 and 64 with 7+8=15
( x + 1 5 ) + ( x ) = ( 4 9 + 1 5 ) + ( 4 9 ) = 1 5
( x ) = ( 4 9 ) = > x = 4 9
The "simpler" is the key word. I´ve tried the first perfect natural squares (1,4,9,16,25,36,49,64) for diference of 15. then 49 is the correct answer.
Using Newton Raphson Method: x i + 1 = x i − f ′ ( x i ) f ( x i ) we find the value of x in six iterations.
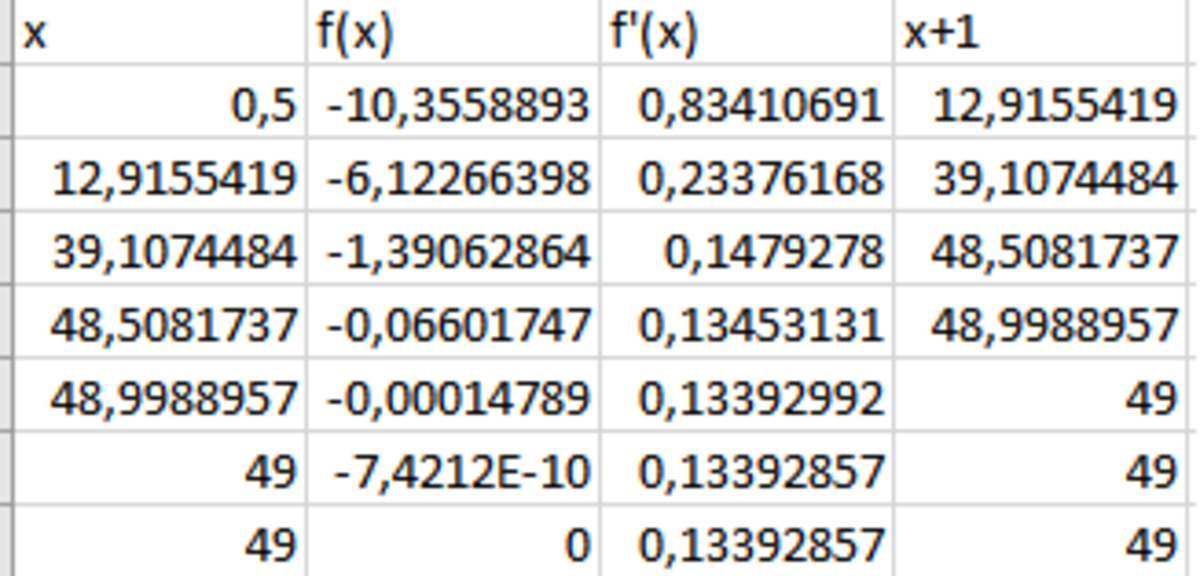
The difference between two consecutive square numbers is an odd number and we now that sqrt(x+15) and sqrt(x) are even numbers so x is a perfect square and x+15 is also a perfect square. (if x wasnt integer the sum would never be integer). So you only have two choices 1 (+3+5+7)= 16 and 49+15=64... well just try 1 and 49 and see that 49 is right
conventional maths is okay. lets try aptitude.
assumption 1: the numbers are perfect square.
think of x such that its a perfect square and adding 15 results in a perfect square too.
we have to test it on 1,4,9,16,25,36,49,64.... (which are perfect squares) 1 and 49 satisfies the condition and 49 satisfies the equation.
√(x+15) + √x=15 √(x+15) + x - 2 √(x+15) √x = 225 (by squaring both sides) or, 2x=210+2 √(x+15) √x or,x=105+√(x+15)*√x or,(x+105)² = x² + 15x or,225x = 11025 so, x = 49
Both √x and x have to be a natural number, so the only options for x are: 1,4,9,16,25,36,49,64,... Knowing that, you can instantly find that x = 49 without any complex calculation, just trial-and-error basis.
- éléver au carrée les deux membres de l'équation;
- mettre les racines dans un membres et les nombres sans racines dans un autre membre;
- éléver au carrée les deux membres et là on obtient une équation sans racine carré de degré 1 après réduction de terme;
- résoudre l'équation de degré 1 et obtenir x=49 après simplification de la fraction obtenue.
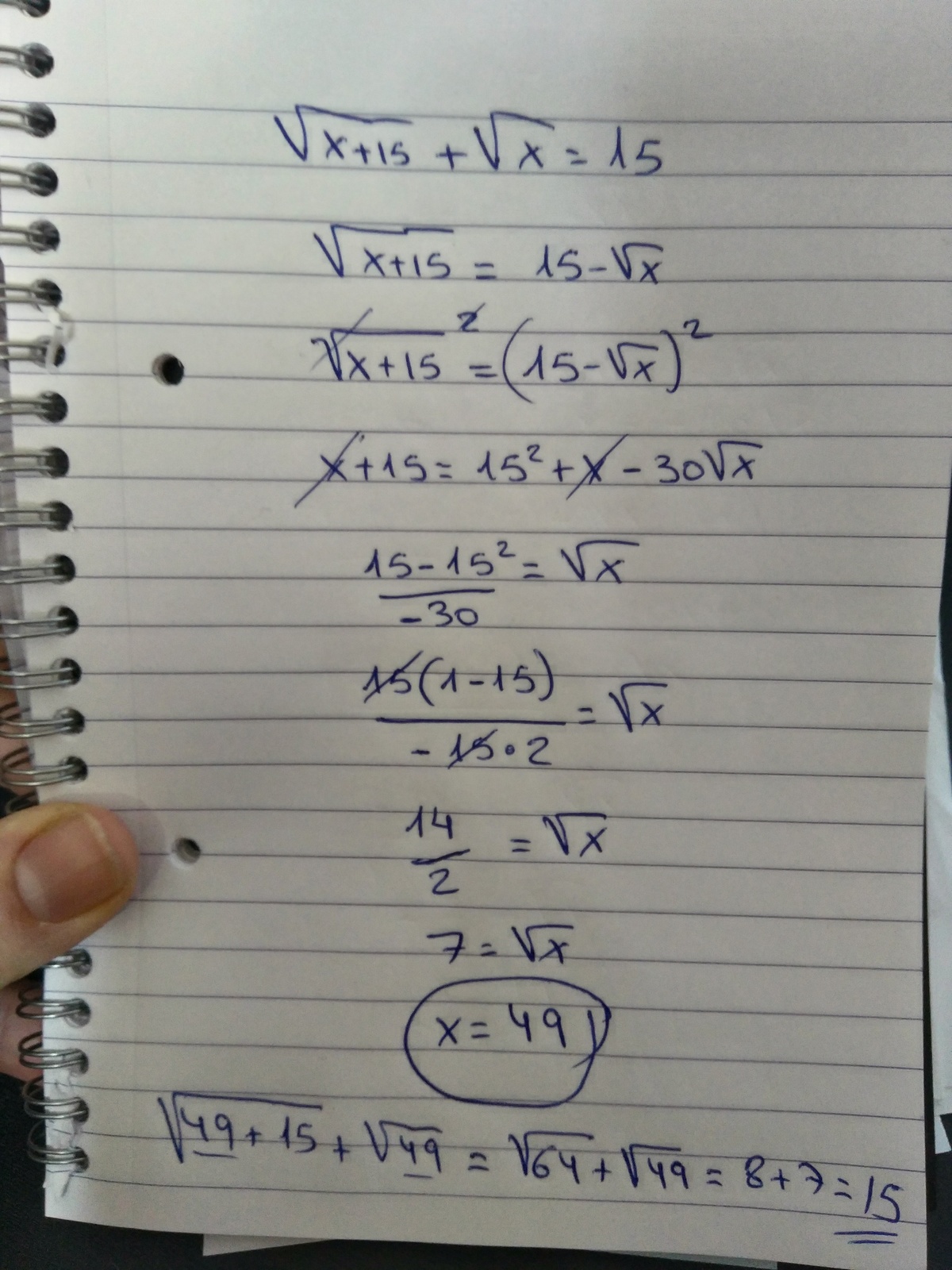
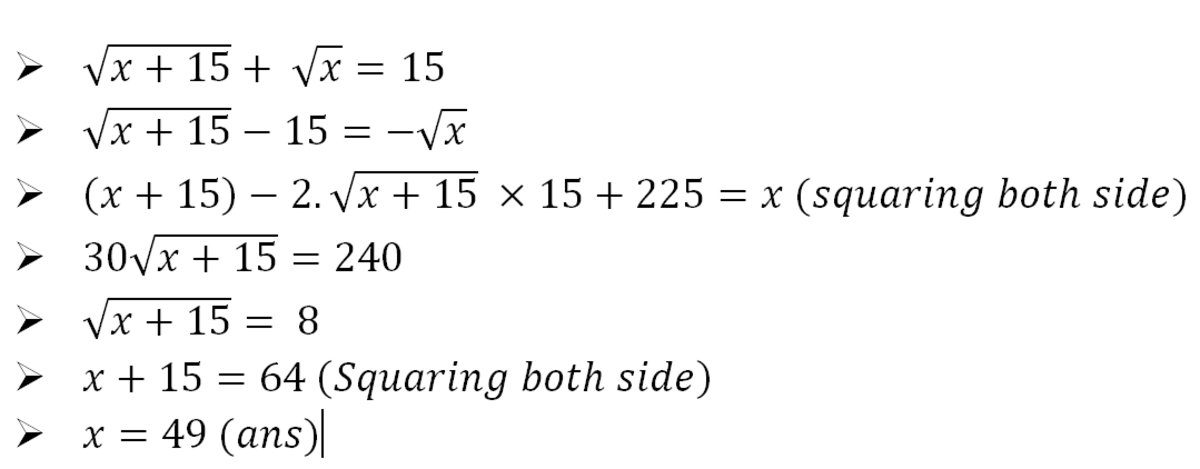
x + 1 5 + x x + 1 5 x + 1 5 3 0 x x ⟹ x = 1 5 = 1 5 − x = 2 2 5 − 3 0 x + x = 2 1 0 = 7 = 4 9 Squaring both sides.