Finding common areas.
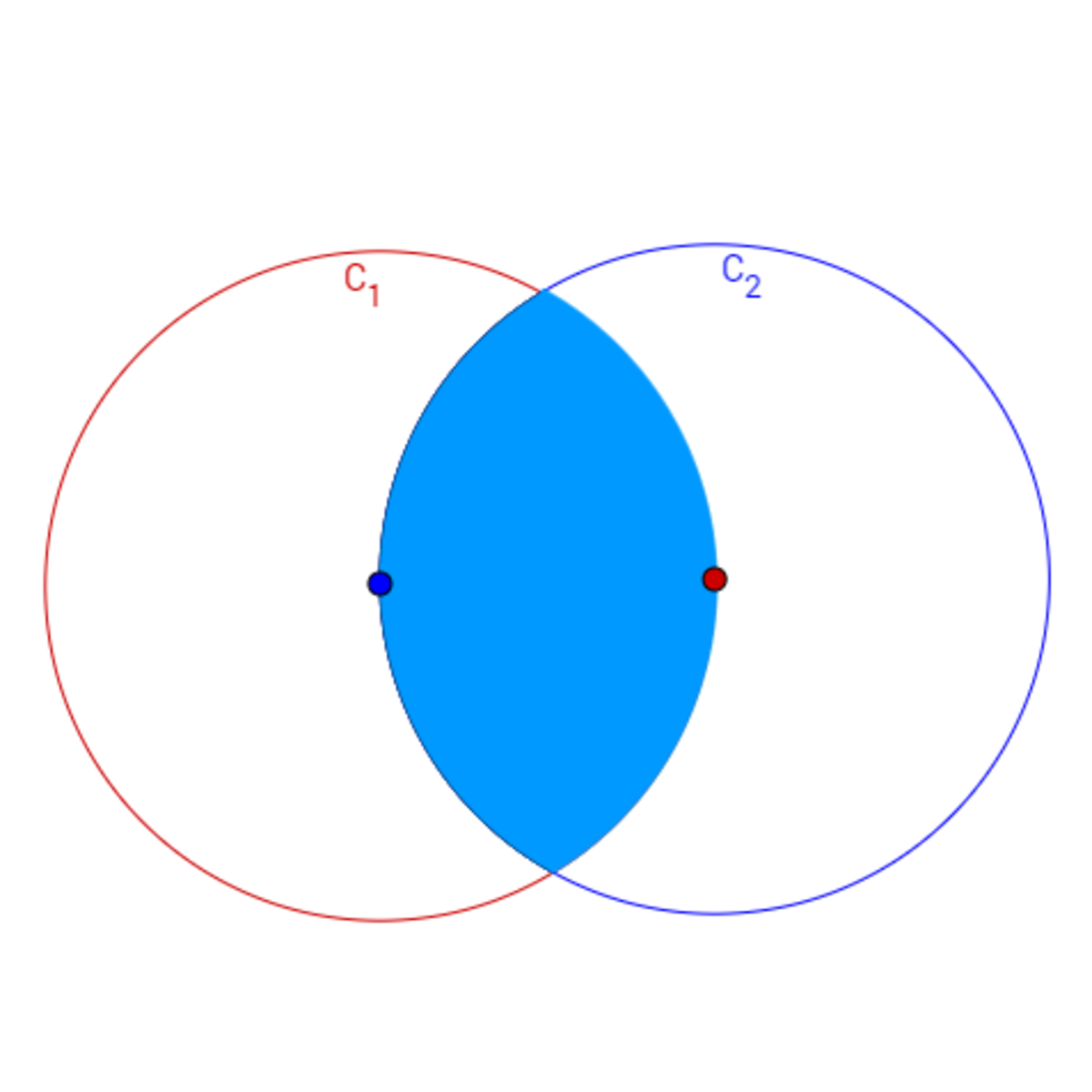
Two congruent circles and of radius intersect at two points such that the center of either circle passes through the center of the other one. If the area of the region common to both circles can be represented as
where and are positive integers and is square free.
Express your answer as .
Details:
- You may need to carry out the necessary subtraction in order to make one common denominator. There is no such restriction to any pairs of integers being co-prime to one another.
- The diagram shown above is just for illustration purposes only.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.

For this question ,
Take one circle's centre at origin O(0,0)and
Other circle centre will be at C(R,0) .
Now x 2 + y 2 = R 2 is one circle equation ......eqn(1)
( x − R ) 2 + y 2 = R 2 is the equation of other circle.......eqn(2)
Subtracting eqn (1) - eqn(2) , we can say that,
They meet at A(R/2,√3R/2) and B(R/2,-√3R/2).
Now to find the area enclosed integrate \sqrt\(R^2-x^2 )dx.
From x=R/2 to x=R . Then we get quarter of the area we required . So,
Now multiply it by 4 .[becase of symmetry]
(Hint : Do integration by putting x=Rsinθ.)
Then we get , R 2 ( 6 4 π − 3 √ 3 ).As answer(area enclosed) .
So, A+B+C+D=15..