Finding the shortest network

If all possible Steiner points exist, the shortest network linking four points is obtained by joining up the points to two Steiner points within the quadrilateral formed by the vertices.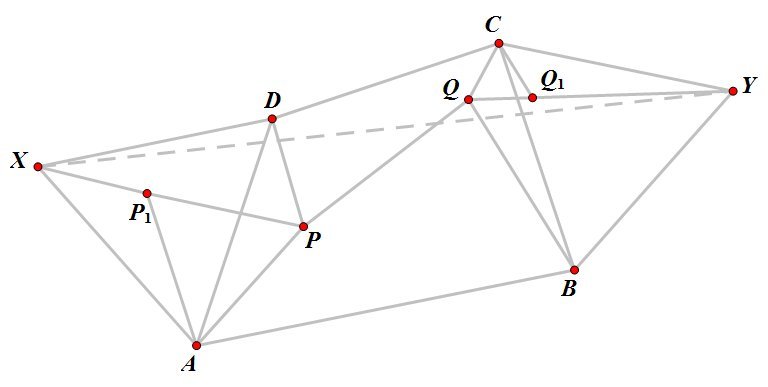 To see how this works, pick points $P,Q$ inside the quadrilateral rotate the triangle $APD$ through $60^\circ$ about the point $A$ to form the triangle $AP_1X$ , thereby creating the equilateral triangle $ADX$ . Similarly, rotate the triangle $CQB$ through $60^\circ$ about $C$ to form the triangle $CQ_1Y$ and the equilateral triangle $CBY$ . Note that $APP_1$ and $CQQ_1$ are also equilateral triangles, and hence $AP + DP + PQ + BQ + CQ \; = \; PP_1 + XP_1 + PQ + Q_1Y + QQ_1 \; \ge \; XY$ and so the length of any network formed by joining $A,D$ to $P$ , $P$ to $Q$ and $B,C$ to $Q$ is greater than or equal to the length $XY$ . Moreover, this length can be achieved if it is possible to choose $P,Q$ such that $P,Q,P_1,Q_1$ all lie on the line $XY$ . This will happen if the angles $\angle APD$ , $\angle DPQ$ , $\angle QPA$ , $\angle PQB$ , $\angle BQC$ and $\angle CQP$ are all $120^\circ$ . 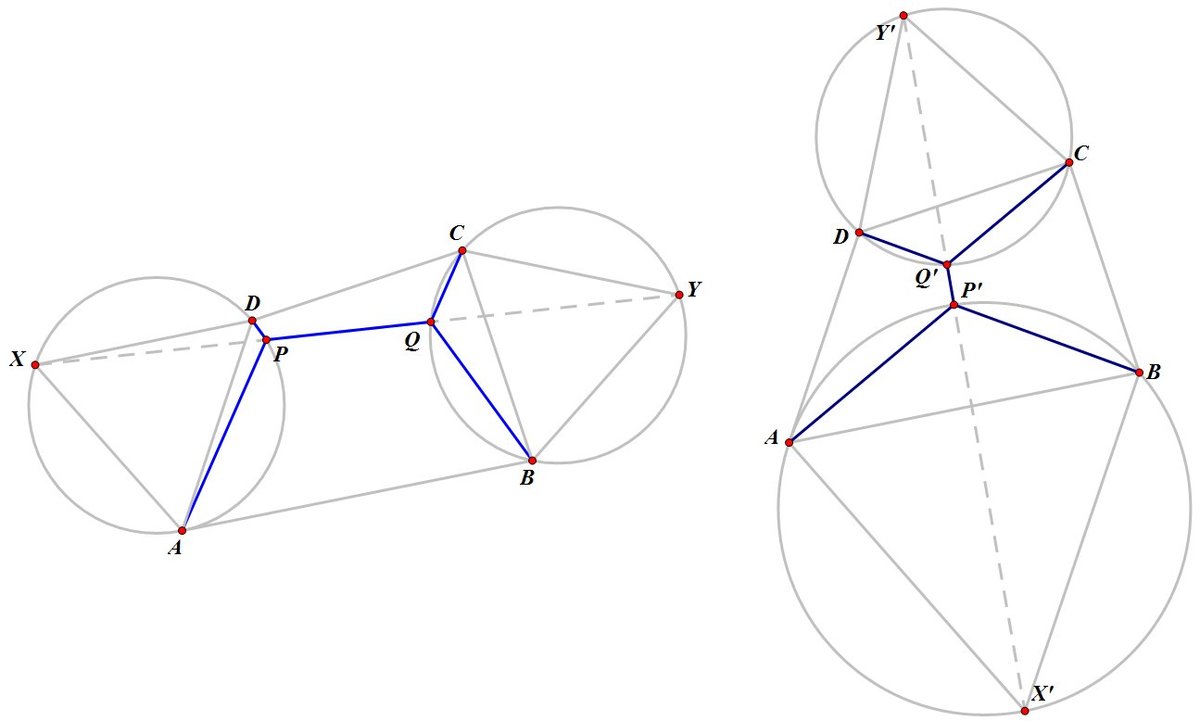The first diagram above shows that this is possible. The second diagram also shows that it is possible to construct a pair of Steiner points if the vertices of the quadrilateral are to be joined in the other pairing. The minimum length of such a network is $X'Y'$ . It remains to show which of $XY$ and $X'Y'$ is the shorter.

It is easy to show that $X,Y,X',Y'$ have coordinates $\begin{array}{rlcrl}X \; & \big(\tfrac12(1-3\sqrt{3}), \tfrac12(3+\sqrt{3})\big) &\hspace{1cm}& Y\; & \big(\tfrac12(9+3\sqrt{3}),\tfrac12(5+\sqrt{3})\big) \\ X' \; & \big(\tfrac12(5+\sqrt{3}),\tfrac12(1 - 5\sqrt{3})\big) & & Y'\; & \big(\tfrac12(5 - \sqrt{3}),\tfrac12(7+3\sqrt{3})\big) \end{array}$ so that $\begin{array}{rclcrcl} XY & = & \sqrt{(4 + 3\sqrt{3})^2 + 1^2} & \hspace{2cm}& X'Y' & = & \sqrt{\sqrt{3}^2 + (3 + 4\sqrt{3})^2} \\ & = & \sqrt{44 + 24\sqrt{3}} & & & = & \sqrt{60 + 24\sqrt{3}} \end{array}$ and so the shortest network has length $XY$ , making the answer $44 + 24 + 3 = \boxed{71}$ .