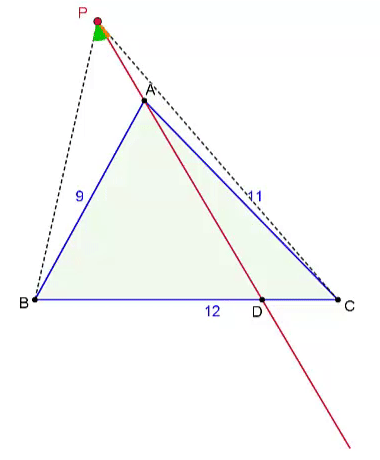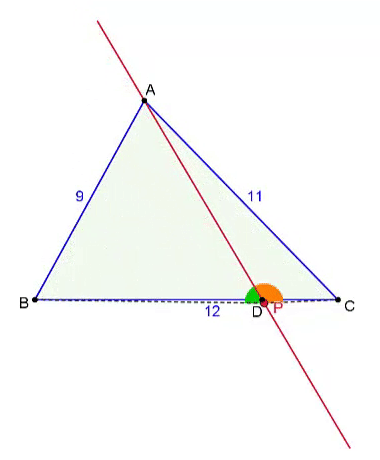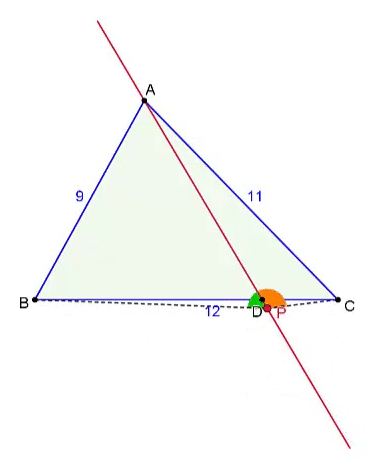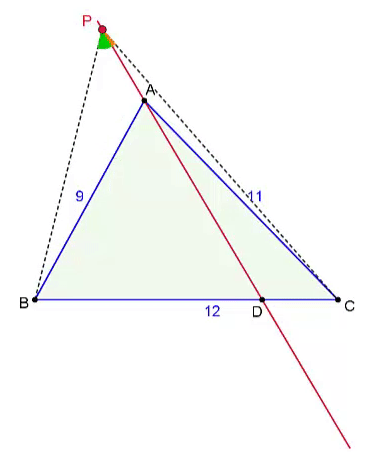
First construct, then find the distances.

Since $BD=3DC$ and $BD+DC=BC=12$ , we have, $BD=9,\; CD=3$ .

Using Stewart's Theorem , in $\triangle ABC$ , $\begin{aligned} AD^2&= \frac{AB^2\cdot CD+ AC^2\cdot BD}{BD+CD}-BD\cdot CD \\ \\ &=\frac{81\cdot 3+121\cdot 9}{12}-27 \\ \\ \therefore \; AD&=\sqrt{84}=2\sqrt{21} \end{aligned}$

Consider point $P$ on line $AD$ such that $\angle BPD=\angle CPD.\;$ Also, $\;\angle CDP=\angle ADB=\angle BAD\implies \triangle APB\sim \triangle DPC$ , $\begin{aligned} \frac{AB}{CD}&=\frac{PB}{PC}=\frac{AP}{DP} \\ \\ \frac{9}{3}=&\frac{m}{n}=\frac{2\sqrt{21}+PD}{PD} \\ \\ \therefore\; PD&=\sqrt{21},\; m=3n \end{aligned}$ Using Stewart's Theorem, in $\triangle PBC$ , $\begin{aligned} PD^2&= \frac{PB^2\cdot CD+ PC^2\cdot BD}{BD+CD}-BD\cdot CD \\ \\ 21&=\frac{3m^2+9n^2}{12}-27 \\ \\ 576&=3(3n)^2+9n^2 \\ \\ \therefore \; n&=4,\; m=12\implies \boxed{m+n=16} \end{aligned}$

---

Construction: To locate point $P$ on line $AD$ ,

• Draw the perpendicular bisector of $BC$ and let it intersect $AD$ at $M$ .

• Draw the circumcircle of $\triangle MBC$ and the intersection point (other than $M$ ) of line $AD$ and the circle gives us the desired point $P$ .

Since $M$ lies on the perpendicular bisector of $BC,\; MB=MC.\;$ Using the fact that equal chords subtend equal angles on the circle, we have, $\angle MPB=\angle MPC\implies \angle BPD=\angle CPD.$

Construction #1

Here is a quick construction: 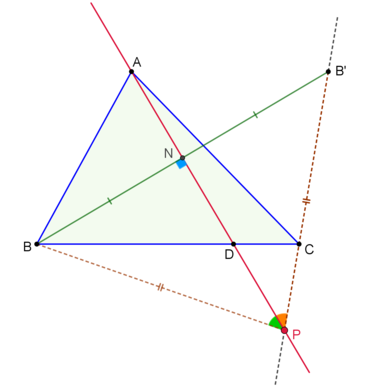Step 1: Reflect point $B$ across line $AD$ and let the image be point ${B}'$ .

Step 2: Draw line ${B}'C$ .

Then, $P$ is the intersection of ${B}'C$ and $AD$ .
Indeed, $\triangle B{B}'P$ is isosceles, with its height $PN$ lying on $AD$ . But this height is also the angle bisector of $\angle BP{B}'$ , hence, $\angle BPD = \angle CPD$ .

---

Construction #2

By Angle Bisector Theorem , it holds that $\dfrac{PB}{PC}=\dfrac{DB}{DC}=3$ Hence, point $P$ lies on an Apollonian circle of segment $BC$ for this ratio. 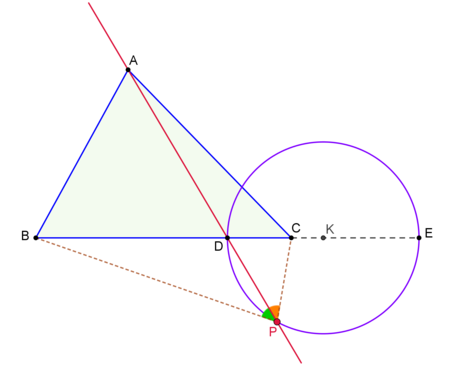Step 1: Construct the harmonic conjugate of $D$ w.r.t. $B$ and $C$ , i.e. extend $BC$ to a point $E$ , such that $BD=DE$ . Indeed, if $BD=DE$ , then $EB=18$ and $EC=6$ , thus $\dfrac{EB}{EC}=\dfrac{18}{6}=3=\dfrac{DB}{DC}$ Step 2: Construct a circle of diameter $DE$ (the Apollonian circle)

Then, $P$ is the intersection of $AD$ and this circle (different than $D$ ).

Indeed, since $P$ belongs to this particular Apollonian circle, it holds that $\dfrac{PB}{PC}=\dfrac{DB}{DC}$ And, by (the converse of) the Angle bisector theorem, $\angle BPD = \angle CPD$ .

Place the diagram on a coordinate system so that $B$ is at $B(0, 0)$ and $C$ is at $C(12, 0)$ .

Since $BD = 3DC$ , and $BD + DC = BC = 12$ , $BD = 9$ and $DC = 3$ , which makes $D$ at $D(9, 0)$ .

Let $A$ have coordinates of $(A_x, A_y)$ . Since $AB = 9$ and $AC = 11$ , by the distance formula $(A_x - 0)^2 + (A_y - 0)^2 = 9^2$ and $(A_x - 12)^2 + (A_y - 0)^2 = 11^2$ , and these two equations solve to $A(A_x, A_y) = A(\frac{13}{3}, \frac{4\sqrt{35}}{3})$ .

The line AD through $A(\frac{13}{3}, \frac{4\sqrt{35}}{3})$ and $D(9, 0)$ then has an equation of $y = -\frac{2\sqrt{35}}{7}(x - 9)$ .

Since $P$ is on $AD$ , let $P$ have coordinates of $P(p, -\frac{2\sqrt{35}}{7}(p - 9))$ .

Since $\angle BPD = \angle CPD$ , by the angle bisector theorem, $\frac{BD}{BP} = \frac{DC}{PC}$ , and since $BD = 3DC$ , then $BP = 3PC$ .

Since $BP = 3PC$ , then by the distance formula, $\sqrt{(p - 0)^2 + (-\frac{2\sqrt{35}}{7}(p - 9) - 0)^2} = 3\sqrt{(p - 12)^2 + (-\frac{2\sqrt{35}}{7}(p - 9) - 0)^2}$ , which solves to $p = \frac{34}{3}$ , and makes $BP = 12$ and $PC = 4$ .

Therefore, $BP + PC = 12 + 4 = \boxed{16}$ .

CDP is similar to BAP , which shows AD =2 DP . Put point E on BD and let BE =3, then AE =2 CP . Use Stewart's Theorem to solve AE =8, then CP =4, BP =3 CP =12