Five and Only Five Spheres
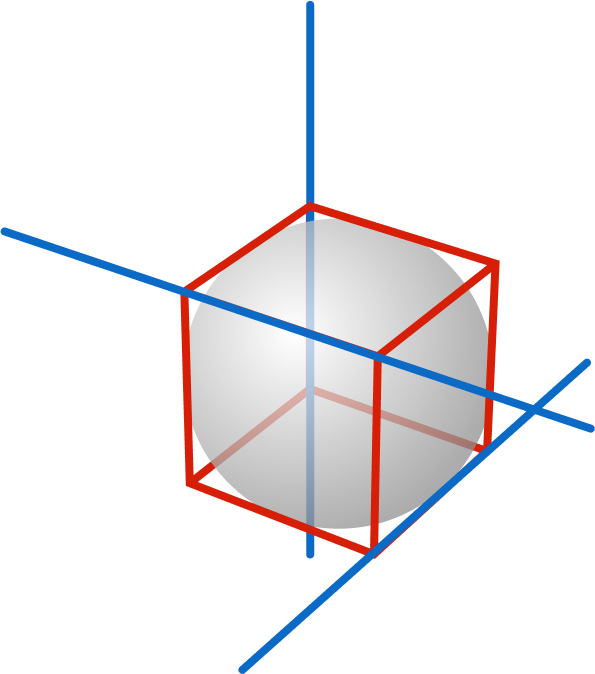
Given a unit cube, extend 3 of its edges into non-intersecting, non-parallel lines (in blue) in 3D space. Then five and only five spheres of the same radius are each tangent to all 3 of the lines.
What is the radius of each of these spheres?
The figure at right illustrates a sphere tangent to the 3 blue lines, but there can only be one such sphere with that radius. (Remember, we need five identical spheres satisfying the tangency condition!)
Suppose the radius of each of the five spheres can be expressed as b a c , where integers a and b are coprime and integer c is square-free.
What is the product a × b × c ?
Note: Spheres may intersect one another.
The answer is 20.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
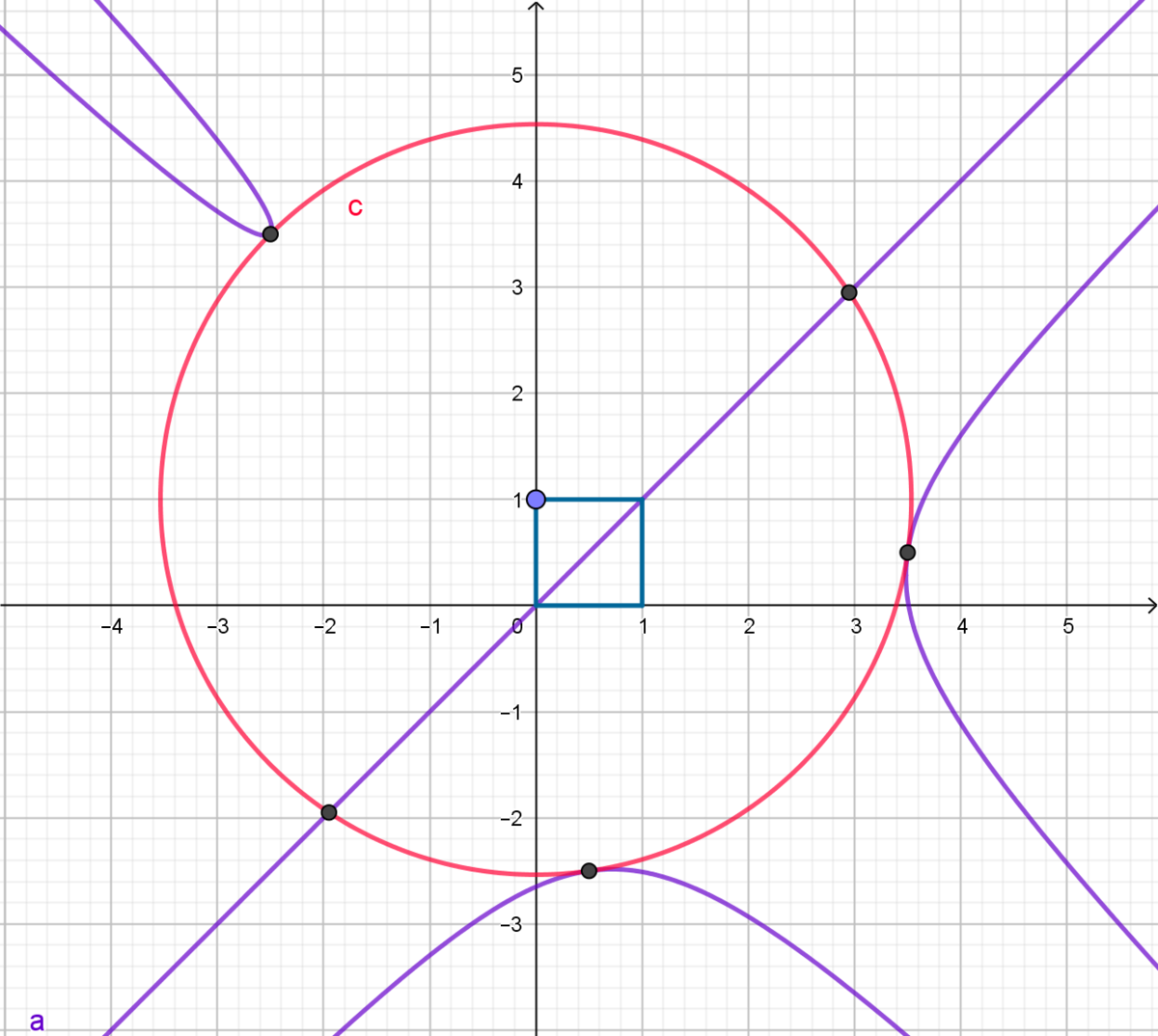
The base of the cube is in blue. The lines are: l 1 : ( 1 , t , 0 ) , l 2 : ( t , 0 , 1 ) , l 3 : ( 0 , 1 , t ) . Euations for sphere center points are x 2 + ( y − 1 ) 2 = r 2 y 2 + ( z − 1 ) 2 = r 2 z 2 + ( x − 1 ) 2 = r 2
By eliminating z we can get the following equation (graphed in purple) ( x − y ) ( x 3 − y 3 − x y 2 + x 2 y − 4 x 2 − 4 x y + 4 x + 4 y − 8 ) = 0
The purple line shows (x,y) coordinates of possible sphere centers. The circle in red shows the case when there are 5 spheres only. They are centered at 5 points indicated and with its centers equidistant to line l 3 .
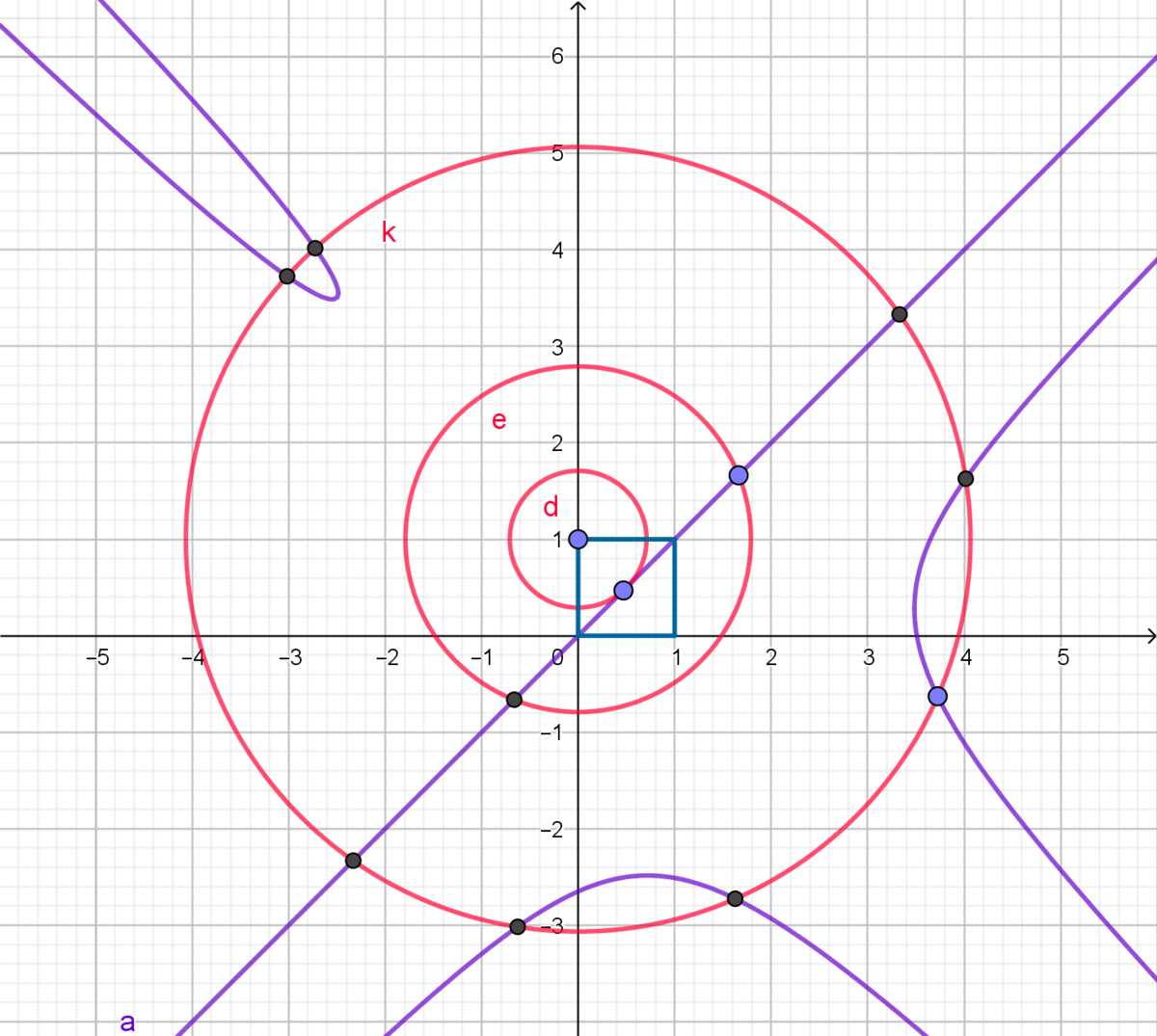
The graph below illustrates other solutions with 1, 2 and 8 spheres.
Log in to reply
Why can't you post that as a solution so that others can see it and I can upvote it? I like the way you've graphically explained how 6 spheres can become just 3 , and uniquely so.
I'll later expand on my own explanation. The other 2 spheres, of course, are centered along the long diagonal of the cube, extended, making it 5 in all.
Log in to reply
I do not have a full solution, just these graphics.
Log in to reply
@Maria Kozlowska – you just did my job for me... showing the succession of possible number of spheres 1 , 2 , 5 , 8
I don't know why I didn't think to use desmos to graph that equation. I would have solved it much faster.
Log in to reply
Actually, I didn't first think of approaching this problem in the way Maria Kozlowska did here. I thought about how 8 spheres in the asymptotic case could be reduced in number as the spheres got smaller, and I realized that 6 of them would become 3 at a particular point, all at the same time because of symnmetry. Then I worked out the radius of that special case using the figure at the top of my solution.
Nevertheless, Maria's solution was a welcome expansion of the analysis of this problem.
We want a sphere with centre ( u , v , w ) and radius k to be tangential to the lines x = 1 , z = 0 y = 1 , x = 0 z = 1 , y = 0 and hence we require ( u − 1 ) 2 + w 2 = ( v − 1 ) 2 + u 2 = ( w − 1 ) 2 + v 2 = k 2 Eliminating v and w from these equations, we obtain the order 8 polynomial for u : 1 6 u 8 − 6 4 u 7 − ( 3 2 k 2 − 1 2 8 ) u 6 + ( 9 6 k 2 − 1 6 0 ) u 5 + ( 2 4 k 4 − 1 7 6 k 2 + 1 0 4 ) u 4 − ( 4 8 k 4 − 1 9 2 k 2 + 1 6 ) u 3 − ( 8 k 6 − 8 0 k 4 + 4 0 k 2 − 3 2 ) u 2 + ( 8 k 6 − 5 6 k 4 − 4 0 k 2 − 4 0 ) u + ( k 8 − 1 2 k 6 − 1 8 k 4 + 4 k 2 + 2 5 ) ( 2 u 2 − 2 u + 1 − k 2 ) ( 8 u 6 − 2 4 u 5 − ( 1 2 k 2 − 3 6 ) u 4 + ( 2 4 k 2 − 3 2 ) u 3 + ( 6 k 4 − 4 0 k 2 + 2 ) u 2 − ( 6 k 4 − 2 8 k 2 − 1 0 ) u − ( k 6 − 1 1 k 4 − 2 9 k 2 − 2 5 ) ) = 0 = 0 Note that the solutions of 2 u 2 − 2 u + 1 − k 2 = 0 correspond to the solutions of the original equations where u = v = w . Other solutions of the original equations will come in triplets ( u , v , w ) , ( v , w , u ) , ( w , u , v ) , and so we can look for a total of 5 solutions by making the sextic term the square of a cubic. Completing the square in the sextic leads to the equation 2 1 ( 2 u 2 − 2 u + 1 − k 2 ) [ { 4 u 3 − 6 u 2 + ( 2 9 − 3 k 2 ) u + ( 2 3 k 2 − 4 5 ) } 2 + 1 6 1 ( 2 k 2 − 2 5 ) { ( 2 4 k 2 + 2 0 ) u 2 − ( 2 4 k 2 + 2 0 ) u − ( 1 6 k 4 + 4 2 k 2 + 3 1 ) } ] = 0 and so we are led to try k 2 = 2 2 5 . When k 2 = 2 2 5 , the order 8 polynomial factorizes as 1 6 1 ( 2 u − 7 ) 2 ( 2 u − 1 ) 2 ( 2 u + 5 ) 2 ( 4 u 2 − 4 u − 2 3 ) = 0 which has exactly 5 solutions for u , and hence for the centres ( u , v , w ) . Thus the required radius is k = 2 5 2 , making the answer 5 × 2 × 2 = 2 0 .
This is monstrous!
Put cartesian cordinantes on the center of the cube, and let the radius be r>0 so that the equations that cordinantes (x,y,z) of the center of a circle must follow are:
(x-1/2)^2+(y+1/2)^2=(x+1/2)^2+(z-1/2)^2=(y-1/2)^2+(z+1/2)^2=r^2
Note that if (u,v,w) is a solution then (u,-w,-v) is also a solution an so are (-w,v,-u) and (-v,-u,w) and thus (v,w,u) and (w,u,v).
Thinking a little bit about this we can see that solutions come in grups of 6 candidates, but among this 6 triplets they can be, either all diferent (which I think will never ocur but indeed we don't care because we would have more than 5), or 3 diferent triplets (of the form (k,-k,0), (-k,0,k) and (0,k,-k) wlog. k>0), or 2 diferent triplets (of the form (q,q,q) and (-q,-q,-q) wlog. q>0), or only one triplet (0,0,0).
To have the case 1 triplet it is clear we need that r=sqrt(2)/2.
To have the case 2 diferent triplets it is clear we need that q=sqrt(2r^2-1)/2 so that it must be r^2>1/2.
To have the case 3 diferent triplets it is clear we need that k=3 and r^2=25/2.
Since r^2=25/2>1/2 so that q=sqrt(2*25/2-1)/2=sqrt(6) in this case we would have as solutions the 3 triplets (3,-3,0), (-3,0,3) and (0,3,-3) and the 2 triplets (sqrt(6),sqrt(6),sqrt(6)) and (-sqrt(6),-sqrt(6),-sqrt(6)) and so is the only way to get 5=3+2 solutions.
Hence r=5/2 sqrt(2)=a/b sqrt(c); a=5, b=c=2 and the answer is simply abc=5*2^2=20.
We start by taking the origin to be at the center of the cube, with the vertices at ( ± 2 1 , ± 2 1 , ± 2 1 ) . Letting the red lines be ⎝ ⎛ α − 0 . 5 0 . 5 ⎠ ⎞ , ⎝ ⎛ 0 . 5 β − 0 . 5 ⎠ ⎞ and ⎝ ⎛ − 0 . 5 0 . 5 γ ⎠ ⎞ , there is a 3-fold rotational symmetry about the line λ ⎝ ⎛ 1 1 1 ⎠ ⎞ , as well as an "antichiral reflection" about the plane r ⋅ ⎝ ⎛ 1 1 1 ⎠ ⎞ = 0 where the structure on one side of the plane is an enantiomorph of the other side (if someone knows the actual name of the reflection, do let me know, thanks :) ).
Observing that the perpendicular distance from any point on the line λ ⎝ ⎛ 1 1 1 ⎠ ⎞ to all the red lines are the same, we can show that as long as the radius of the sphere, r, is greater than or equal to 2 1 , there exists a sphere tangent to all 3 lines whose center lies along this line. Due to the reflection symmetry, there exists another sphere of the same radius whose center also lies along this line but on the other side of the plane, as long as the sphere is not centered on the origin. Hence if r > 2 1 is satisfied, we will have 2 spheres tangent to the lines.
Because of the 3-fold rotational symmetry and the reflection symmetry, any sphere we find that does not lie on the line or the plane will have 5 other identical copies also tangent to the lines. However, assuming r > 2 1 is satisfied, we only need 3 more spheres. Hence we should find a sphere that lies on the plane such that it is only affected by the rotational symmetry to produce exactly 3 spheres in total. Considering a point ( a , b , c ) that lies on the plane, we can form a system of linear equations in a , b , c and r using the constraint that a + b + c = 0 and the perpendicular distances to each line all equal r. This gives us the following system of equations:
a + b + c = 0 ( a + 0 . 5 ) 2 + ( b − 0 . 5 ) 2 = r 2 ( b + 0 . 5 ) 2 + ( c − 0 . 5 ) 2 = r 2 ( a − 0 . 5 ) 2 + ( c + 0 . 5 ) 2 = r 2
Solving this and rejecting negative values of r, we get one set of solutions for r = 2 1 , which corresponds to the sphere pictured in the question, and 3 sets of solutions for r = 2 5 , which correspond to the 3 more spheres we need. Since r > 2 1 is satisfied, we also have the 2 spheres that lie on the axis of symmetry hence we have a total of 5 spheres.
This also explains the possible number of spheres we can get; 1 sphere centered on the origin if r = 2 1 , 2 spheres whose centers lie on the axis of symmetry and equidistant to the origin for 2 1 < r < 2 5 , 5 spheres where 2 lie along the axis and 3 on the plane of antichiral reflection for r = 2 5 and 8 spheres where 2 lie along the axis and 6 spheres that result from the 3-fold rotation and antichiral reflection symmetries for r > 2 5 . Intuitively, for the case where 2 1 < r < 2 5 , there can't be a set of 3 spheres tangent to all 3 lines not lying along the axis of symmetry simply because it is too small to reach a third line, and for the case where r > 2 5 , any other loci outside the axes and the 6 described by the symmetries would either be too close to the line and intersecting it, or too far and not touching it. Maria Kozlowska's comment under Michael Mendrin's solution provides a more rigorous analysis of the possible loci of sphere centers which describes these cases with more detail.
Nice intuitive solution, this doesn't have that annoying algebraic nightmare of an under-determined system of equations. It's also pretty interesting to note that a , b , c happen to have integer solutions
The radius r is 2 5 2
which is found by solving the equation
2 ⎝ ⎛ r 2 − ( 2 1 ) 2 − 1 ⎠ ⎞ = r
Refer to this figure for derving the above equation to solve for r of the sphere tangent to the 3 blue lines, and such that its center is on the same plane that is halfway between the top and bottom planes of the cube. The green circle of radius r touches the vertical blue line.
Had the radius of this sphere been smaller than 2 5 2 , the sphere about where it is could not be tangent to those 3 lines. If greater, then 2 spheres about there could be tangent to them.
The longer solution involves showing that, depending on the radius of the spheres, there can either be 8 , or 5 , or 2 , or 1 sphere(s) that are all tangent to the 3 lines. In particular, while there is a range of values possible for 8 or 2 spheres, for 5 and 1 sphere(s) there is exactly only one radius, namely 2 5 2 and 2 1 2 , respectively.
See Maria Kozlowska's figures showing the succession of possible number of spheres 8 , 5 , 2 , 1 explained in more detail in her comments below. Based on her equations, here are the 3D locus in purple of the centers of all the spheres that can be tanget to all 3 straight blue lines. The cylinder of radius 2 5 2 with one of the blue lines as the axis touches these 4 purple lines in exactly 5 places (one purple line intersects the cylinder in 2 places). Refer to Maria's comments about that.
and here's the 3D illustration of the Five Spheres