Five Hexagons
Five identical regular hexagons are inscribed without overlap inside a regular hexagon of side length 1 .
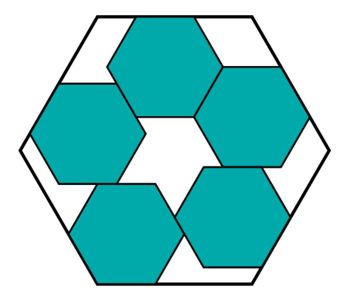
The sides of length s of the five identical hexagons is the largest possible. Find s .
The answer is 0.375.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
A slip. It is 6-gon.
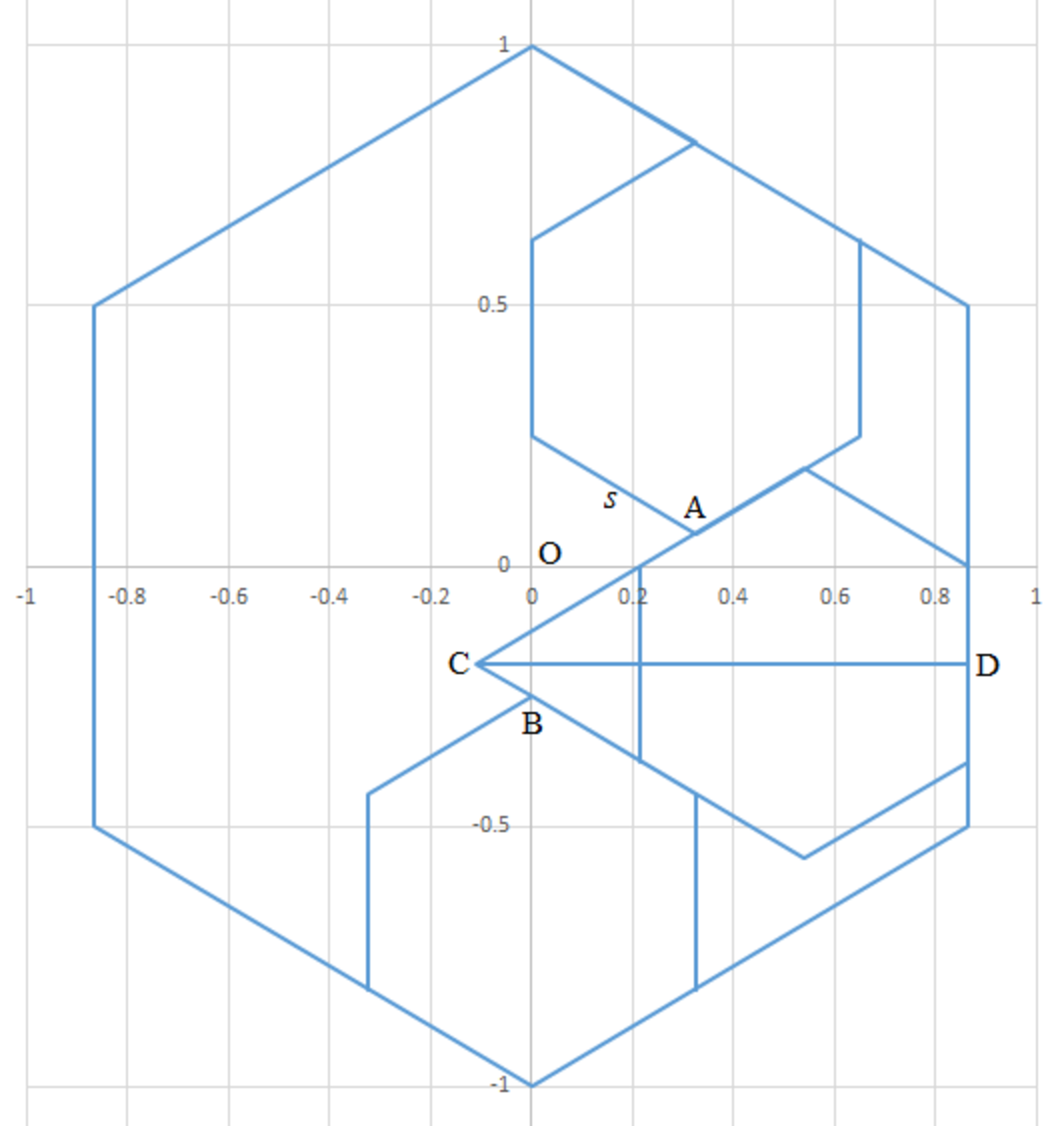
Turn the large unit regular hexagon by 3 0 ∘ counterclockwise. Let the center of large unit hexagon be the origin O ( 0 , 0 ) .
Then the bottom vertex of the top small hexagon is at A ( 2 3 s , 1 − 2 5 s ) . And the line C A is on x − 2 3 s y − 1 + 2 5 s = 3 1 ⟹ y = 3 x − 3 s + 1 .
Similarly, the top vertex of the bottom small hexagon is at B ( 0 , 2 s − 1 ) , and C B is on y = − 3 x + 2 s − 1 . Then the x -coordinate of C is 3 2 x = 5 s − 2 ⟹ x = 2 3 ( 5 s − 2 ) . The line C D has a length of 2 3 − x and this fit in 2 3 3 s . Therefore,
2 3 − x 2 3 − 2 3 ( 5 s − 2 ) 1 − 5 s + 2 ⟹ s = 2 3 3 s = 2 3 3 s = 3 s = 8 3 = 0 . 3 7 5
This is definitive. Thank you.
Isn’t it a turn by 3 0 ∘ counter clockwise?
Log in to reply
Yes, you are right.
Log in to reply
Nevertheless, it is a nice solution!
Log in to reply
@Thanos Petropoulos – Glad that you like it.
Answer from Figure is 6/16=0.375 For formal proof, write two equations, one for conservation of length and another for area:
(1)3s-b=1, s is side of green hexagons.
(2) Large hexagon area= 5 (green hexagon area of size s)+8 (equilateral triangle of size s)+2* (trapezium smaller)+4*(trapezium larger)
Solve the two equations for s and b.
Answer is s=3/8
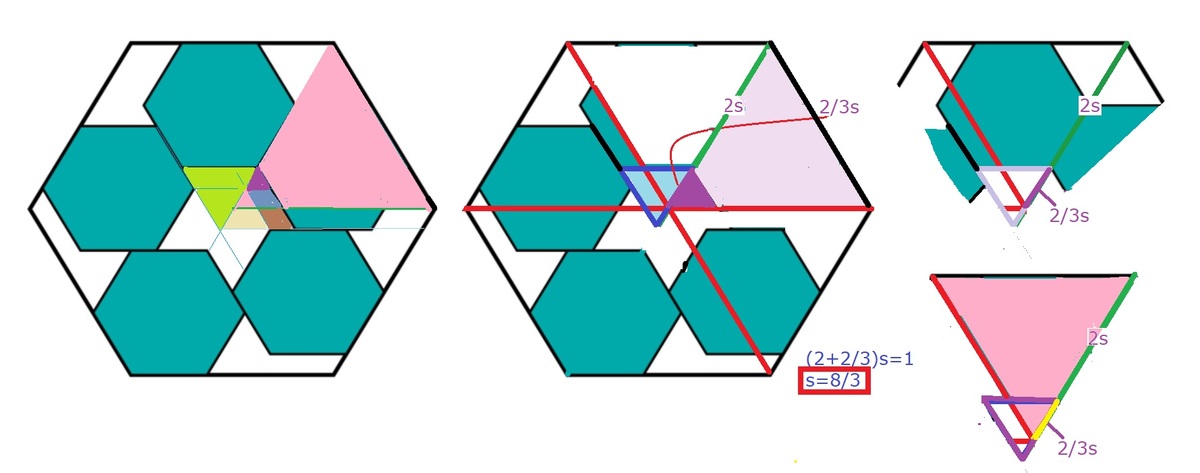
Then we can see ( 2 x ) × 6 + 4 x = 6 u n i t s
⇒ x = 1 6 6 u n i t s = 0 . 3 7 5 u n i t s