Five towns... Minimal roads
Five towns (Abra, Bulbasaur, Charmander, Dratini, and Eevee) happen to be located on the corners of a regular pentagon with side length of 1 km as shown here as A, B, C, D and E:
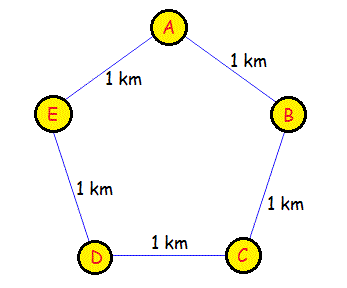
You, as an urban planner are in charge of planning a road that connects the five towns with the least possible road distance.
What is the least possible road distance (in kilometers) that you can use?
Give your answer to 2 decimal places.
The answer is 3.89.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The most curious thing about Steiner trees is that given n points, there always seem to exist at least one Steiner tree. I haven't been able to find an exception, even in 3 dimensions.
Log in to reply
How about for three colinear points?
Log in to reply
Not counting trivial cases, where nodes coincide with the vertices themselves.
Log in to reply
@Michael Mendrin – Hmmm... What is the Steiner tree for a heptagon?
Log in to reply
@Geoff Pilling – That can be constructed in a fairly straightforward day. Let me first go have my dinner and then I'll get back to you on that.
Log in to reply
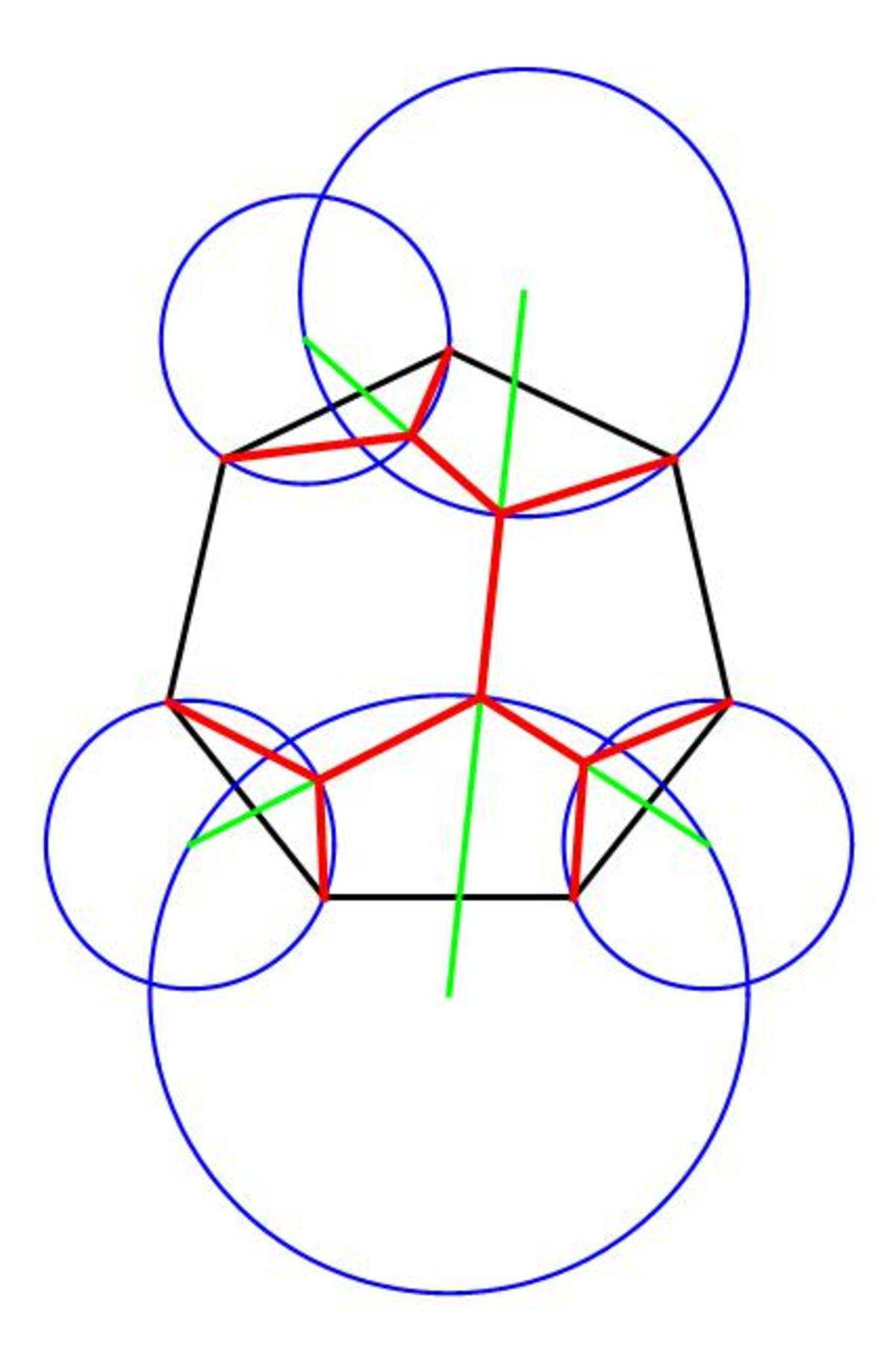
@Michael Mendrin – Okay, here it is, the Steiner tree is in red. Green lines and blue circles are intermediary construction steps that help find the location of the Steiner tree. All the 3-way connections are at 120 degree angles.
Edit: PUBLIC NOTICE---THIS GRAPHIC IS ERRONEOUS!
Log in to reply
@Michael Mendrin – Have you checked that this network is minimal? See my other note.
Log in to reply
@Mark Hennings – It's a Steiner tree, i.e., a network of lines connected at nodes at 120 degree angles. It's at least a local minimum, i.e., any perturbation results in a longer total path.
Log in to reply
@Michael Mendrin – I wonder... Is there a theorem that determines how many different Steiner paths can be created from a collection of n points?
Log in to reply
@Geoff Pilling – Let's not make this subject any more complicated just right now!
@Michael Mendrin – Is it? If all the red lines were at 1 2 0 ∘ to each other, then various pairs of red lines in the hexagon on the left would be parallel to each other, and they do not seem to be so. This may be a distortion of the way the graphic is presented (but the circles do look circular, so the distortion cannot be that great).
Log in to reply
@Mark Hennings – Oh, I need to make an adjustment to fix that, I see my oversight now with one of the steps. For the 2D case, the construction should be simpler.
I'll get back to this a little later today.
Log in to reply
@Michael Mendrin – Okay, here's the revised graphic. It's easier doing this using Mark Hennings' suggestion.
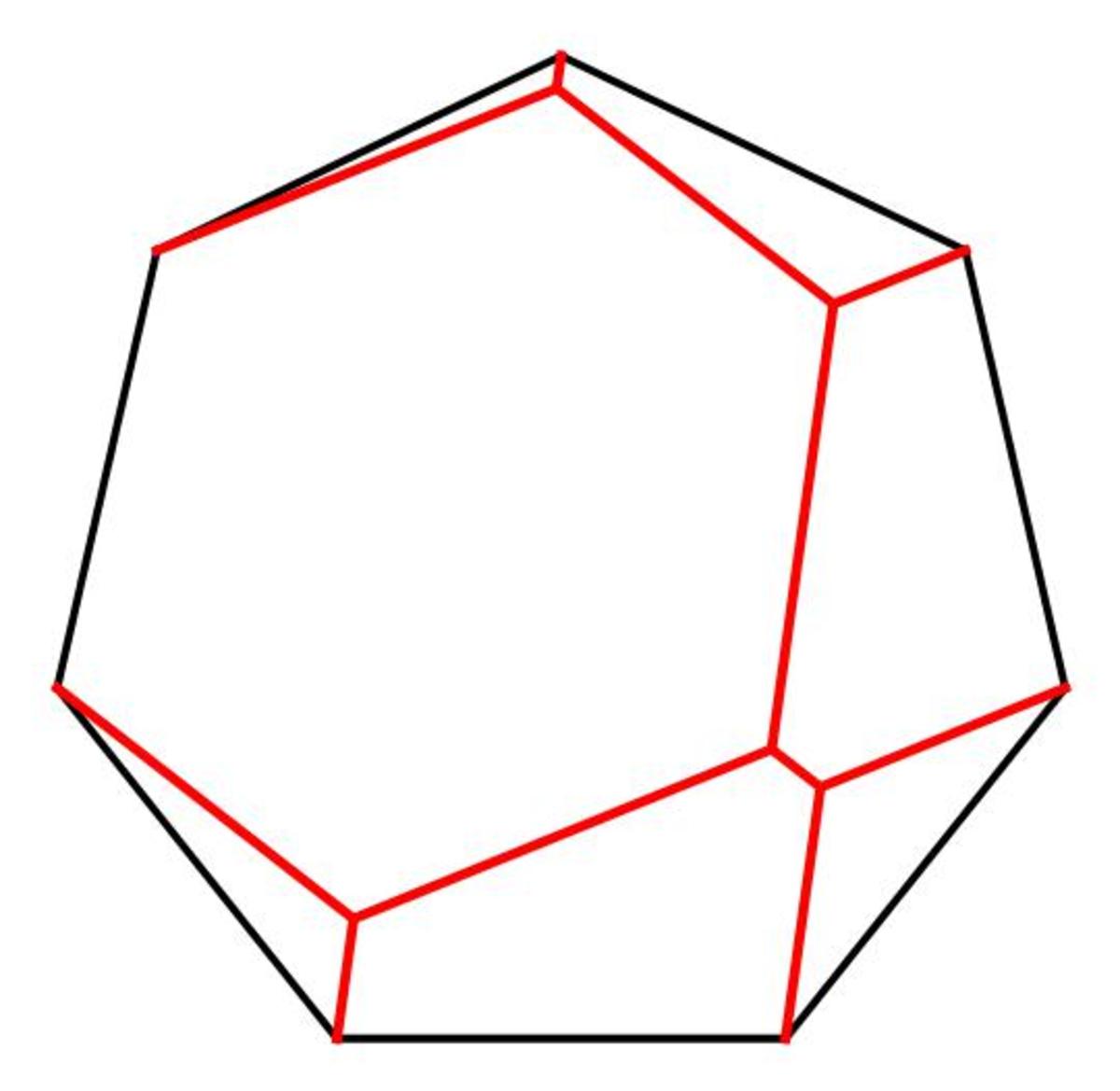
The critical angle seems to be 8 2 . 0 8 3 1 5 . . . degrees, the angle which the near-vertical red lines make with the horizontal line that includes the base of the heptagon. The other two angles are 1 2 0 degrees apart as usual.
The total length of the red path is 6 . 5 4 1 2 8 . . . , which is greater than 7 − 1 = 6 , if the sides of the heptagon is 1 . In this case, the simple path around the perimeter beats the Steiner tree.
Log in to reply
@Michael Mendrin – The frustrating thing is that the 1934 paper which proves the minimum network for most polygons is freely available, but written in a language like Romanian that I cannot read, and the more recent paper that fills the 7-12 gap is not open access.
@Michael Mendrin – Interesting... Thanks for posting, @Michael Mendrin !
@Michael Mendrin – I think you will find the the shortest network on a regular n -gon (with n ≥ 7 ) is simply n − 1 of the sides. Minimal distance networks with Steiner points only exist on regular n -gons if n ≤ 6 .
The result was proved by Jarnik and K"ossler in 1934 for n ≥ 1 3 , and completed for 7 ≤ n ≤ 1 2 by Du Hwang and Wen
Log in to reply
@Mark Hennings – What do you make of the figure I have provided here? Is there a shorter path where the lines come together at angles not 120 degrees, other than along n − 1 of the sides of the heptagon (the trivial case where the nodes coincide with the vertices)?
The point I'm raising is that there always seem to exist a Steiner tree, even if it isn't necessarily the shortest possible path. For other configurations of 7 points, such a Steiner tree would exist, and could be the shortest possible path. The papers cited addresses only regular n − gons.
It's been often said that soap bubbles always form shapes with the least surface area. Technically, that's actually not true---they form shapes with the least surface area LOCALLY, i.e., they form stable surfaces that cannot perturb to another with less area. For example, two soap bubbles can either join with a common face, or become one bubble, with the latter having the least total area for a given total volume.
Log in to reply
@Michael Mendrin – We have to be careful of assuming that Steiner networks are automatically shortest length. If we consider an irregular, but not too wild, quadrilateral, there are two different Steiner networks possible (the four vertices can be paired up with the two extra vertices in two different ways), but one of these has greater length than the other
I understand that, in general, the business of finding a Steiner network for a set of points is an NP-hard problem. That should indicate the level of difficulty involved here!
There are a number of papers investigating the problems of Steiner networks for regular polygons plus their centre. This problem admits a variety of solutions for a wide variety of polygons
Log in to reply
@Mark Hennings – My method of "constructing" a Steiner tree still works, the adjustment I needed to make is to put the ends of the green lines slightly elsewhere. As I said, it was an oversight.
However, as we are both saying, a full Steiner tree isn't guaranteed each time (we could run into degenerate cases where the Steiner nodes coincide with the vertices), and even when found, it isn't necessarily the global minimum.
This problem was posted 2 months ago, with an excellent detailed solution by @Julian Poon .
Ooops, I didn't realize that the problem had already been posted. I agree with @Mark Hennings that the solution is much more complete than mine. Perhaps I should remove this problem? (So we don't have two floating around?)
Log in to reply
I should let it stay. There have been multiple posts before... It is always worth searching for a keyword or two before posting a new problem, just in case it has been done recently.
This is an example of a Steiner tree problem .
It turns out that the only Steiner tree for a regular pentagon (not counting rotations) is represented here:
Lines shown in green represent the road. Black lines are for reference only.
Solving for the distance:
Total distance = 2 1 1 7 + 7 5 + 3 9 0 + 1 7 4 5 ≈ 3 . 8 9 km (when rounded to 2 decimal places)
Image and problem credit: http://puzzling.stackexchange.com/