Floating in Mercury
Before, a ball was floating in liquid mercury. After, water has been poured on the ball until the ball is entirely submerged.
How has the ball's position changed?

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Guys the ball submerged! That means it is heavier than water, in this case it will fall down. I think question answer is wrong
Log in to reply
the diagram was incorrect, i changed it. thanks for pointing it out.
the conclusion is still correct though.
Log in to reply
Doesn't that depend on the density of the ball? If the ball is denser than water but not denser than murcury how would the water improve the balls boyancy? the ball is surely displacing it's volume in water, but weight in mercury. Does the waters weight push on the mercury but not the ball somehow? I seriously don't understand the physics of this problem, and the explanation you posted describes a completely seperate situation as far as I can tell. Could you go more basic in your explanation AND describe the asked for situation rather than if you replaced water with mercury. (also please tell us comparable density between mercury, ball and water in the problem).
Log in to reply
@Gustaf Carstam – there are in depth calculation on the other solutions, my solution is more "intuition-based".
notice that when the ball rise, regardless of the density of the ball, mercury level should drop (my original diagram is a bit misleading). intuitively, the water push against the mercury, forcing mercury on higher level to fill in lower part of the ball, which force the ball to rise.
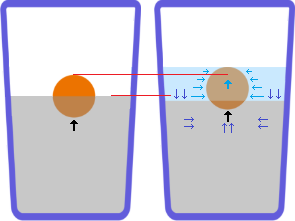
my "what if" situation is not completely separated. (by contradiction) lets assume the water push the ball and cause it to sink, then the same reason should apply to more mercury (or liquid X with same density as Hg), which cause the ball to sink, isnt that absurd?
Lets use a a familiar example. You are holding your friend off of the ground, he is very heavy and difficult to hold up. Now, you both get into a deep pool and you pick your friend up off the floor of the pool, he now seems lighter and easier to lift. The buoyancy force is what makes your friend feel lighter in the pool. Now relate this experience in the pool to the problem above: you are the mercury, holding up your friend, the ball, and the addition of water increases the bouyancy force making him feel lighter.
If there was a vacuum on top of the mercury, would the ball be less submerged?
Log in to reply
i believe the ball will be lowered (i guess it means more submerge?)
Log in to reply
So if the air above the ball was to be pressurized, the ball would rise?
Another case of What if: suppose the water has the same density as the ball (a water balloon would be a close approximation): the ball will lie entirely on top of the mercury. I.e. it definitely has moved up.
Log in to reply
Further to that, I guess, if the mercury was to become less dense the ball would drop.
Better yet, "What happens if the density of that band of air is continuously increased until it has the density of mercury. What will the ball do in the meantime?" Rise continuously, of course.
A nice quick illustration explaining why the ball would rise.
Mercury is denser than water. Therefore it is possible for an object to float in mercury but sink in water.
So since water is heavier than air, wouldn't the water increase the pressure on the ball from the top and push the ball further down into the mercury?
Log in to reply
Let's say there's only water in the cup. When a steel ball is dropped into the water, the water isn't "pushing the ball down". In fact, because water pressure increases with depth, the net force on the ball is actually upwards. This the reason why a steel ball in water weighs less than a steel ball in air.
alternatively, (by contradiction) lets assume the water push the ball and cause it to sink, then the same reason should apply that more mercury will push the ball to sink, isnt that absurd?
As a partial, but direct, answer: Yes, the pressure in the water will try to push the ball down more than the air was trying to push the ball down.
However, that same increase in pressure by adding the water is also going to try to push the mercury down, increasing the pressure in the mercury, which means the mercury will now be pushing up on the ball more than it was with just the air.
Since we get a higher downward force from the water but also a higher upward force from the mercury, this argument is actually inconclusive to the movement of the ball.
It does say 'the ball is entirely submerged'...
NICE EXPLANATION.I got it right using my mechanics logic but this solution is the best bet!
Ohhhhhhhhhh...
But what if the ball is denser than water (so that it doesn't float up) while being able to float in Mercury? The option should be rise or remain at the same level.
Log in to reply
it would still be rise. to see why, consider some liquid whose density between air and water, such that ρ air < ρ ball < ρ water
now insert the "picture" between the first ("before") and second ("after") picture. hopefully that clears up.
Good question. If you ignore the mercury, wold the ball weigh more or less with water added. It would weigh less. So in the case as described in the puzzle, when water is added the ball would exert less pressure on the mercury because of the added buoyancy because of the water and thus float in higher or exert less downward force on the mercury. YOU GOT ME on this one. JcGilmour.ca
Without the water, the weight of the mercury displaced by the ball and the "air" (or none) displaced by the ball equals the weight of the ball.
W 1 M e r c u r y + W A i r = W B a l l
With the water, the weight of the mercury displaced by the ball and the weight of the water displaced by the ball equals the weight of the ball.
W 2 M e r c u r y + W W a t e r = W B a l l
or
W 1 M e r c u r y + W A i r = W 2 M e r c u r y + W W a t e r
Neglecting W A i r , we have
W 2 M e r c u r y = W 1 M e r c u r y − W W a t e r
so that the fraction of the ball in the mercury is reduced.
This assumes that 1) the ball is in hydrostatic equilibrium, and 2) is less dense than mercury but denser than both water and air.
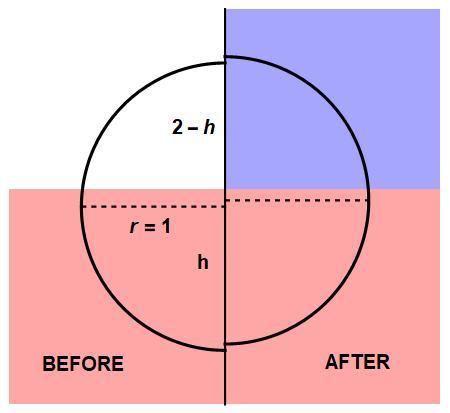
Let's figure this out for a steel ball of unit radius
Let the relative densities of mercury, steel, water, and air be approximately 1 3 . 5 , 8 , 1 , 0 . Then, using the formula for the volume of a Spherical Cap , we have two equations, the first one with just mercury and air, and the second with mercury and water
1 3 . 5 3 π h 2 ( 3 r − h ) + 0 3 π ( 2 − h ) 2 ( 3 r − ( 2 − h ) ) = 8 3 4 π r 3
1 3 . 5 3 π h 2 ( 3 r − h ) + 1 3 π ( 2 − h ) 2 ( 3 r − ( 2 − h ) ) = 8 3 4 π r 3
with h being 1 . 1 2 4 0 9 and 1 . 0 8 0 1 7 with the mercury and air and with mercury and water. Thus, relative to the level of the mecury, the steel ball is slightly higher when submerged in water.
In the equilibrium "before", the buoyant force is equal to the weight of displaced fluid (Archimedes' Principle).
If the ball would remain in place, the weight of displaced fluid would be greater "after", since water is more dense than air. Thus the buoyant force increases, forcing the ball upward.
But if the weight of the water displaced is much less than the weight of the part of the volume of the ball that does the displaceing of said water, does the buoyant force on the ball increase enough? You have demonstrated that the buoyant force is larger in water than in air, but you haven't in my opinion demonstrated that the buoyant force is enought to actually cause the ball to rise up. If the density difference between mediums is big enough then would the ball not have a larger decrease in buoyancy from the mercury (as it displaces less) than the increase in buoyancy from the water (when it displaces more) causing the ball to not rise at all?
Log in to reply
What do you mean? There is more upwards force if the equilibrium is unchanged, so the equilibrium has to change...
Even if the density of the ball is 99.9999% of that of mercury, it will still move upwards by a small amount if the upper layer of fluid is changed from air into water. Yes, it will be hard to observe in reality, but the effect is still there. And for a more realistic density of the ball, the effect should be easy to see.
If the ball did not rise, the buoyant force would be greater than the weight of the ball. The ball is therefore no longer in equilibrium and will accelerate upward.
No one told me in the ball wa air...
No one explained it all as far as I can see. the key is to realize that since the ball is less dense than mercury, it will have less downward force pushing on it by the water then on the mercury.
Mercury is denser than water. If the ball floats in mercury, it will definitely float in a liquid less denser than mercury, in this case, water.
This is backwards. More things will float in the denser fluid than the less dense fluid.
In the 'after' case, should the ball stay in the same position, the downwards pressure on the mercury would be higher than that on the ball because the water is shallower above the ball. Thus the ball would slightly rise.
The buoyant force before and after is the same, because in both cases the ball is supposed to be floating. Then, we have: V i ⋅ ρ H g = V f ⋅ ρ H g + V w a t e r ⋅ ρ w a t e r ⇒ V f = V i − ρ H g V w a t e r ⋅ ρ w a t e r Where V i and V f are the initial and final volume of the ball in mercury, respectively. And we can, clearly see that the final volume is less than the initial volume, so we can deduce the ball has risen its position.
That is wrong. The buoyant force depends on the volume of the ball which is submerged. Before, the ball was floating on Hg and was only partially immersed. After, the ball is completely covered by water. Thus there is more upwards buoyant force on it. Its mass is unchanged, therefore the downwards gravitational force is unchanged. As net force upwards has increased, the ball must accelerate upwards (thank you Newton).
Ignore my comment. It is incorrect. Here is the real situation:
Both before and after, the ball is at rest and therefore the upwards (buoyant) and downwards (gravity) forces are equal in magnitude and opposite in direction.
The mass of the ball is constant and thus the downwards gravitational force is constant.
Therefore the total upwards buoyant force must be constant. This buoyant force equals g x the mass M of fluid displaced. g is constant, thus the mass M of fluid displaced must be constant.
Before, the ball displaced some mass M of Hg. After, the ball displaces the same mass M of (Hg + water). The ball displaces some mass m of water, so it must therefore necessarily displace mass M-m of Hg. M-m < M (because m is > 0), thus the ball displaces less Hg after the water is added.
The only way the ball can displace less Hg is to rise. QED.
It is true that as the ball rises, the Hg surface drops a bit. But the Hg fall < the ball rise, both because Hg is denser than the ball (we know this because the ball floats on Hg) and because of geometry (cross sectional area of sphere is always < cross sectional area of larger diameter cylinder).
Part of the ball is now in water. It exoeriences upward force equal to volume of water displaced. Therefore goes up.
Buoyant force is always equal to the weight of the displaced fluid. In both cases, forces are balanced and thus the buoyant force equals the weight of the ball. The weight of the ball is constant, which means that the buoyant force must also be constant (as the ball has no net force in either case). In the second case, there is more total volume of fluid that the ball dispaces, and so it must displace LESS of the denser fluid which would have a greater weight per volume of displacement. The ball must rise, so that buoyant force can reimain constant.
SURFACE TENSION , MERCURY HAVE HIGH COHESIVE FORCE (FORCE BETWEEN MERCURY MOLECULES) THAN ADHESIVE FORCE (FORCE BETWEEN MERCURY AND GLASS) , THUS MERCURY DONT WET GLASS , WHEREAS WATER WET GLASS , THAT IS , WATER HAVE MORE ATTRACTION TOWARDS ANY MATERIAL (SUCH AS GLASS OR ANY BALL) THAN MERCURY THUS WHEN WATER IS POURED , WATER WILL ATTRACT THE BALL , THUS BALL WILL ARISE.
Suppose the position of the ball is constant after,then the part in the air turns into the part in the water whose density is greater.And because the buoyancy equals the gravity of the ball,it is impssible that the ball stay still which means that the total buoyancy after exceeds the gravity of the ball.As a result,the ball has to rise to reduce the buoyancy so that it equals the gravity of the ball.
consider 3rd case, replace water with more mercury and imagine the result, the answer will become pretty obvious.