Floor function equation
x ⌊ x ⌋ = y
For how many integer values of y , where 1 ≤ y ≤ 2 0 1 7 , are there real values for x which satisfy the equation?
The answer is 1973.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
What i did : plotted graph of x [x] , then finded points on y axis correspondig to points of discontinuity (integer y ) on both sides of axes . Took out the uncommon points finded 37 y 's from 1981 to 2017 did not have an real x. Please point out where i am wrong.
Log in to reply
Bro you are missing some points , I also did by graph and got correct answer(44 discontinuities)
Log in to reply
Hi Bro. Can you tell me a value of x for which y=1981
I first carefully examined the graph and include a snapshot of the bottom:
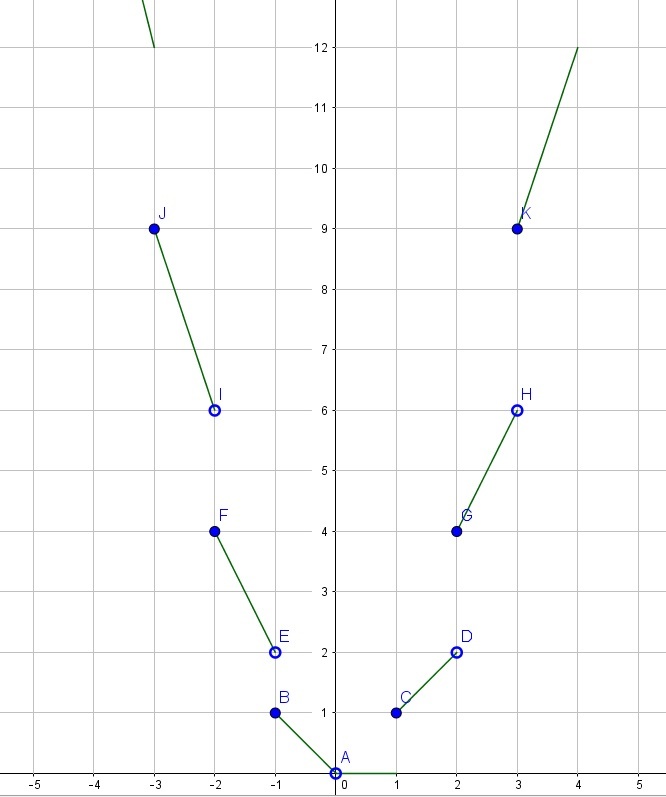
It became clear that if y was a perfect square number, then there were TWO solutions for x .
If y was of the form n 2 + n , then there was NO SOLUTION for x .
If y was any other number, then there was a SINGLE solution for x , sometimes + , sometimes - .
In the range of values for y, from 1 to 2017 inclusive, we find 44 perfect squares.
2 0 1 7 − 4 4 = 1 9 7 3
This solution is not as rigorous or detailed as @Brian Moehring provides (which I upvoted - thanks, Brian) but it provides a visual way of seeing the problem.
Your solution is easy to grasp ,sir. (+1)!
Instead of focusing on x , let's focus on n : = ⌊ x ⌋ and ε : = { x } . Note that n can be any nonzero integer and ε ∈ [ 0 , 1 ) , and both of them can be chosen independently of one another. In these new terms, we have ( n + ε ) n = y ⇒ n y = n + ε ∈ [ n , n + 1 ) .
Now, if n > 0 , this implies y ∈ [ n 2 , n 2 + n ) = [ n 2 , n 2 + ∣ n ∣ ) , and if n < 0 , this implies y ∈ ( n 2 + n , n 2 ] = ( n 2 − ∣ n ∣ , n 2 ] . Combining these, y is an integer such that there is a positive integer m = ∣ n ∣ such that, y ∈ ( m 2 − m , m 2 + m )
More explicitly, y ∈ m ∈ N + ⋃ ( m 2 − m , m 2 + m ) = ( 0 , 2 ) ∪ ( 2 , 6 ) ∪ ( 6 , 1 2 ) ∪ ⋯ where the observation that the right endpoint of one open interval and the left endpoint of the next open are the same can be confirmed by verifying m 2 + m = ( m + 1 ) 2 − ( m + 1 ) for all m ∈ N + .
Finally, we have the way to find our answer: The only positive integers which cannot be the y -value are those integers of the form m 2 + m for some m ∈ N + . Solving 1 ≤ m 2 + m ≤ 2 0 1 7 ⇒ 1 ≤ m ≤ 4 4 so y cannot be 4 4 numbers out of the 2 0 1 7 positive integers in that range, so there are 2 0 1 7 − 4 4 = 1 9 7 3 possible such values for y .