Flower-like loop
The figure shows a circular loop of radius R (black curve) that has been harmonically deformed into a flower-like curve (blue curve) given by the equation in polar coordinates r ( θ ) = R ( 1 + ε cos ( n θ ) ) with ε = 0 . 5 and n = 5 .
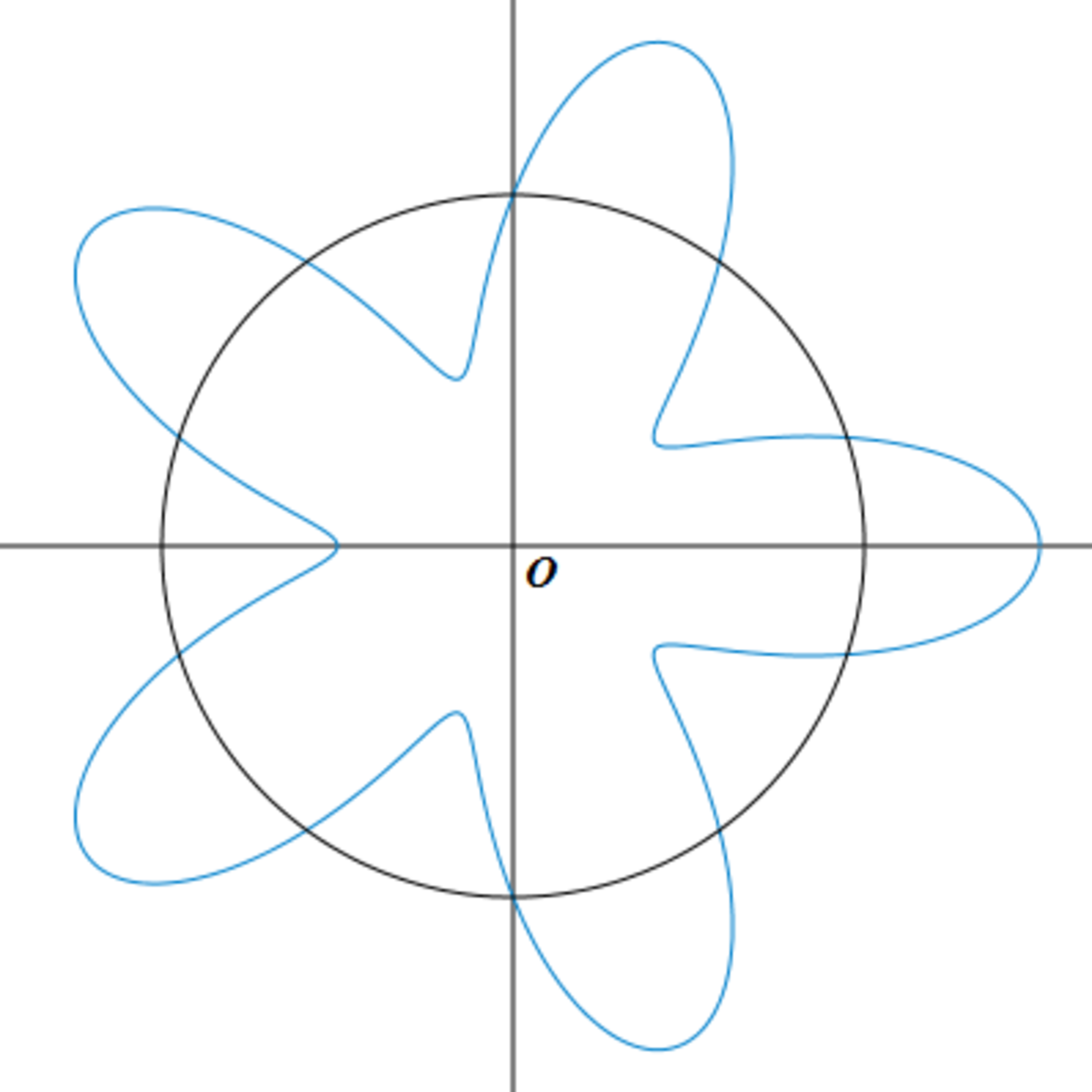
A current I 0 flowing in the circular loop produces a magnetic field B = 1 mT at the center O. Determine the magnitude of the magnetic field in mT at O when the same current, I 0 , flows in the flower-like loop. The following integral may be useful: ∫ 0 2 π 1 + ε cos ( x ) d x = 1 − ε 2 2 π .
The answer is 1.15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
I think you made a raw assumption here that d l × r = ( r d θ ) ( r ) . The other two solutions explain how it was got .
how can you directly say that cross product of d l × r is rdθ * r without taking into account the angle between them??
Log in to reply
Ok, it was my fault, I thought it was obvious and didn't explain, thanks for your comments.
I will explain it here:
Because it's cross product, ∣ d l × r ∣ will be the product of r and the component of d l which is perpendicular to r , so it is ( r d θ ) r .
Log in to reply
this is really nice!!! (i really sweated it out finding the equation of tangent and then finding perpendicular distance from center. I was actually considering component of r perpendicular to d l , i should have thought the other way round.)
I actually found this problem quite easier than the other ones. Simple integration stuff. :)
Nicely done Dinh!
The Biot-Savart equation is given by:
B = 4 π μ 0 I 0 ∫ C r 2 d l × r ^
We can write the line element of a circuit in the z = 0 plane in cylindrical coordinates as:
d l = d r r ^ + r d θ θ ^
Then the cross product d l × r ^ in the Biot-Savart law is:
d l × r ^ = ∣ ∣ ∣ ∣ ∣ ∣ r ^ d r 1 θ ^ r d θ 0 z ^ 0 0 ∣ ∣ ∣ ∣ ∣ ∣ = − r d θ z ^
B = 4 π μ 0 I 0 ∫ C r 2 − r d θ z ^
∣ ∣ ∣ B ∣ ∣ ∣ = 4 π μ 0 I 0 ∫ C r d θ
In the circular loop case r ( θ ) = R :
∣ ∣ ∣ B 1 ∣ ∣ ∣ = 4 π μ 0 I 0 ∫ 0 2 π R d θ
∣ ∣ ∣ B 1 ∣ ∣ ∣ = 2 R μ 0 I 0
In the flower-like curve case r ( θ ) = R ( 1 + ε c o s ( n θ ) )
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 4 π μ 0 I 0 ∫ 0 2 π R ( 1 + ε c o s ( n θ ) ) d θ
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 4 R π μ 0 I 0 ∫ 0 2 π 1 + 2 c o s ( 5 θ ) d θ
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 4 R π μ 0 I 0 3 4 π
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 2 π R μ 0 I 0 3 2 3
∣ ∣ ∣ B 2 ∣ ∣ ∣ = ∣ ∣ ∣ B 1 ∣ ∣ ∣ 3 2 3
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 1 m T × 3 2 3
∣ ∣ ∣ B 2 ∣ ∣ ∣ = 1 . 1 5 m T
Let us consider a small current carrying element at an angle θ at a distance r from center.Let us assume center to be ( 0 , 0 ) and let the coordinates of this element be ( x 0 , y 0 ) . Now let us extend this element as a big line and let p denote the length of perpendicular dropped on this line from origin.Since, the small magnetic fields of these elements are in same direction, we can simply add their magnitudes.
∣ d B ∣ = 4 π r 3 μ 0 I 0 ∣ d l × r ∣ = 4 π r 3 μ 0 I 0 p d l ... ( i )
Let f ′ ( x ) denote the slope of this element.
By simple trigonometry , d l = d x 1 + ( f ′ ( x ) ) 2 ..... ( i i )
Now, let us write the equation of extended line :
y − y 0 = ( x − x 0 ) f ′ ( x ) ,
Hence , p = 1 + ( f ′ ( x ) ) 2 ∣ y 0 − x 0 f ′ ( x ) ∣ ... ( i i i )
From ( i i ) and ( i i i ) , we get :
p d l = ∣ y 0 d x − x 0 d y ∣ ,
Here, use x 0 = r c o s θ , and y 0 = r s i n θ , take derivative and simplify to get
p d l = r 2 d θ . Put this value in ( i ) to get :
∣ d B ∣ = 4 π r μ 0 I 0 d θ = 4 π R ( 1 + η c o s ( n θ ) ) μ 0 I 0 d θ
⇒ B = 2 π B c i r c l e ∫ 0 2 π 1 + η c o s ( n θ ) d θ = 1 . 1 5 B = 1 . 1 5 m T
For a current I 0 flowing in a curve C , the magnetic field at the point r is B ( r ) = 4 π μ 0 I 0 ∮ C ∣ r − s ∣ 3 d s × ( r − s ) Thus the field at the origin is B ( 0 ) = 4 π μ 0 I 0 ∮ C ∣ s ∣ 3 s × d s = 4 π μ 0 I 0 ∫ 0 2 π s d θ k where k is a unit vector normal to the plane.
For the circular loop the magnitude of the magnetic field at O is B 1 = 4 π μ 0 I 0 ∫ 0 2 π R d θ = 2 R μ 0 I 0 = 1 mT For the flower-like loop the magnitude of the magnetic field at O is B 2 = = = 4 π μ 0 I 0 ∫ 0 2 π R ( 1 + ε cos n θ ) d θ 4 n π R μ 0 I 0 ∫ 0 2 n π 1 + ε cos θ d θ 4 π R μ 0 I 0 ∫ 0 2 π 1 + ε cos θ d θ = 2 R 1 − ε 2 μ 0 I 0 or 1 − ε 2 1 = 3 2 = 1 . 1 5 mT.
This would be a derivation for noob :D Starting from Biot Savart’s law d B = 4 π r 2 μ I d l × r ^ Multiply r for both nominator and denominator and make use of the relation r ^ = r hence,
d B = 4 π r 3 μ I d l × r = 4 π r 3 μ I ∣ ∣ ∣ d l × r ∣ ∣ ∣ B ^ Where B ^ is the unit vector of B Observing the quantity ∣ ∣ ∣ d l × r ∣ ∣ ∣ , it is the area of the parallelogram constructed from the two vectors. This area is twice the area of the triangle which is formed by the two vectors. The dimensions of this triangle are r, r, and dl. Using Sine rule, this area is 2 1 r 2 d θ . Hence, ∣ ∣ ∣ d l × r ∣ ∣ ∣ = r 2 d θ
d B = 4 π r 3 μ I ∣ ∣ ∣ d l × r ∣ ∣ ∣ B ^ = 4 π r 3 μ I r 2 d θ B ^ = 4 π r μ I d θ B ^
∣ ∣ ∣ B ∣ ∣ ∣ = ∫ 0 2 π 4 π r μ I d θ = 4 π μ I ∫ 0 2 π R ( 1 + ϵ cos ( n θ ) ) d θ = 4 n π R μ I ∫ 0 2 n π ( 1 + ϵ cos ( n θ ) ) d ( n θ ) = 4 π R μ I ∫ 0 2 π ( 1 + ϵ cos ( n θ ) ) d ( n θ ) = 4 π R μ I 1 − ϵ 2 2 π = 1 − ϵ 2 B d u e t o c i r c u l a r l o o p = 3 2 ≈ 1 . 1 5
According to Biot-Savart's law: d B 0 = 4 π μ 0 r 3 I 0 d l × r .
Therefore, d B 0 = 4 π μ 0 r 3 I 0 ( r d θ ) r = 4 π μ 0 r I 0 d θ = 4 π R μ 0 I 0 1 + ε cos ( n θ ) d θ
Therefore, B 0 = 0 ∫ 2 π 4 π R μ 0 I 0 1 + ε cos ( n θ ) d θ .
B 0 = 2 R 1 − ε 2 μ 0 I 0 = 1 − ε 2 B = 1 . 1 5 ( m T ) .