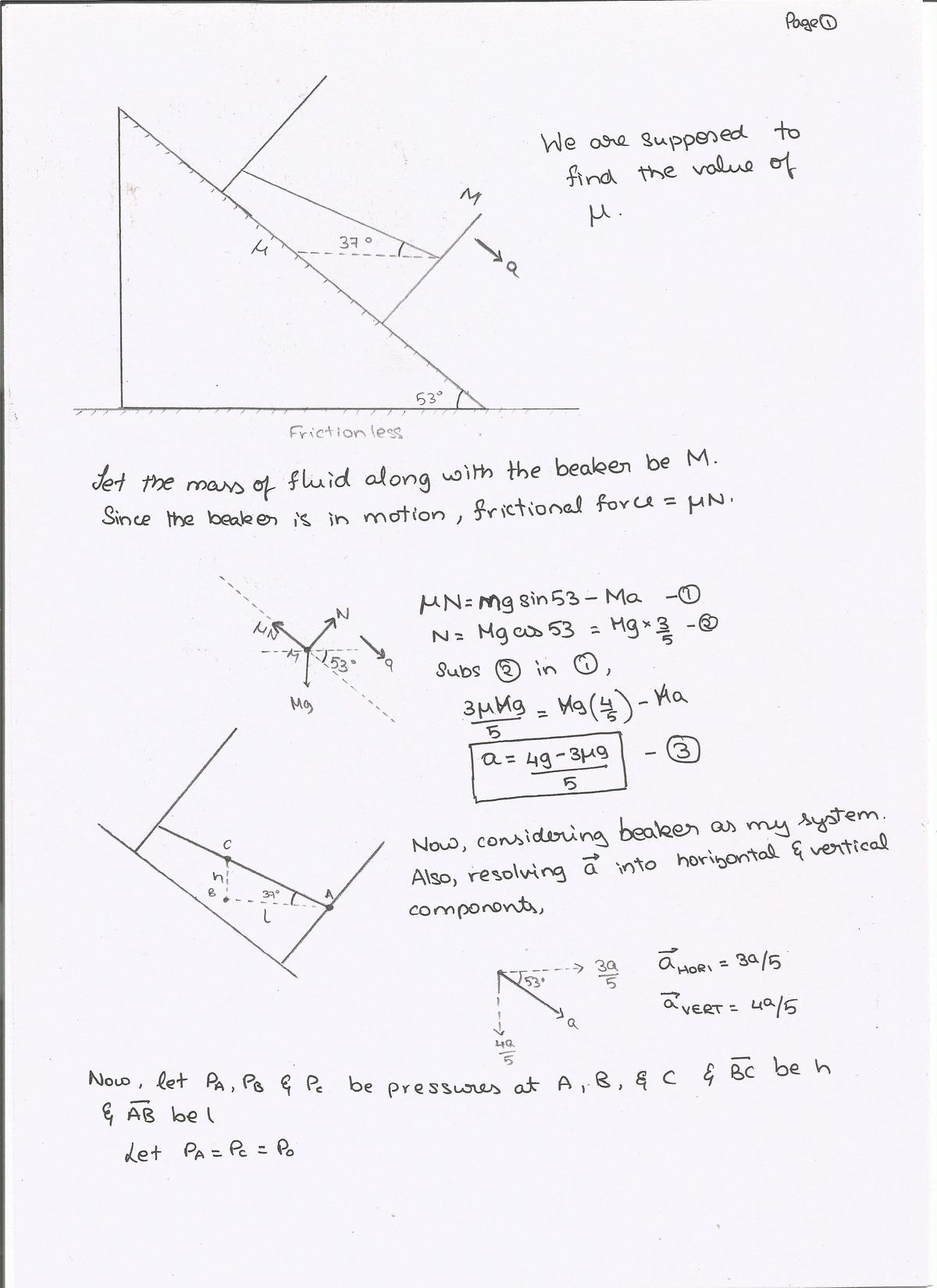
Fluids on incline
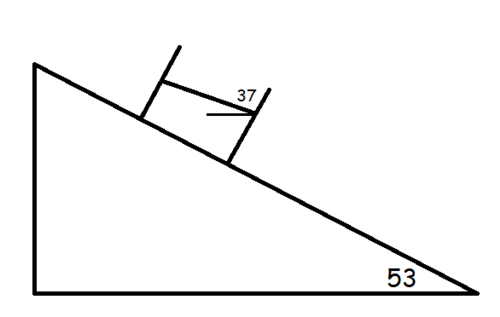 A container filled with liquid moves down a rough fixed inclined plane with constant acceleration as shown in figure above.
A container filled with liquid moves down a rough fixed inclined plane with constant acceleration as shown in figure above.
The angle of incline is cos − 1 5 3 and the liquid surface makes an angle of cos − 1 5 4 with the horizontal.
If the coefficient of friction can be written as b a where a , b are coprime positive integers, find a + b .
The answer is 31.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
The exact solution of the problem is tan 1 6 ∘ ≈ 0 . 2 8 7 , which cannot be written as the fraction of integers. You want us to assume that tan 5 3 = 4 / 3 , but that is not obvious.
I have a much shorter solution for you, but because I could not solve the problem, I cannot post it as a regular solution.
Anyway, here it is: First, I work with the local inertial frame of reference of the container, so that the force of gravity can be ignored. I choose the x-axis parallel to the incline. The angle between the liquid surface and the horizontal is now 53 - 37 = 16 degrees. This angle is due to the contact force on the container (normal force and friction).
The normal force is m g cos 5 3 ∘ in the y-direction, and the friction force is μ m g cos 5 3 ∘ in the x-direction. The resultant force is perpendicular to the liquid surface, and therefore makes a 16 degree angle with the vertical. This gives tan 1 6 ∘ = F y F x = μ . The friction coefficient is therefore μ = tan 1 6 ∘ ≈ 0 . 2 8 7 .
Log in to reply
I did it the same way but yes, I approximated the value of t a n 5 3 to be 3 4 and value of t a n 3 7 to be 4 3 then use t a n ( A − B ) to calculate t a n 1 6 . (all angles are in degrees)
However, It should be mentioned in the question to take t a n 5 3 = 3 4 and t a n 3 7 = 4 3 and the incline is fixed.
Don't tell me u dint assume it to be 3/5 nd 4/5 ... lol
Log in to reply
No I didn't... Because it is only an approximation.
Why force of gravity can be ignored?
Log in to reply
I chose a coordinate system in free fall. Relative to that coordinate system, there is no gravitational force, and the container is accelerated upward by the normal force from the incline.
Log in to reply
@Arjen Vreugdenhil – oh.. fine.. nice one bro!
Thanks. I have edited the problem for clarity.
In future, if you spot any errors with a problem, you can “report” it by selecting "report problem" in the menu. This will notify the problem creator who can fix the issues.
Log in to reply
Thanks. 8 months ago I was not aware of the Reporting feature, but now I am :) In fact, nowadays I'd even do the edit myself
Consider Any Small Point Mass On The Surface Of Liquid . Since A Liquid Cannot Sustain Shear Stress
Therefore The Mass Must Be In Equilibrium Along The Surface Of Liquid. We Work From The Frame Of
Beaker . Resolving Pseudo Force And Weight Of Mass Along the surface of liquid and equating them We Get
4-3x = 3/cos16
For Finding value of cos16 we use trigonometric identity cos(53-37)
On Solving We Get x = 7/24
Although It Should Have Been Mentioned But We Here Use
cos53 = 3/5
cos37 = 4/5
Because Mostly Indian Students Will Know This Approximation .
@Prakhar Bindal - I didn't get why did u took cos16.can u explain plz
In case of any discrepancy, feel free to comment.