Flux (7/3/2020)
An open surface is defined as follows:
4 x 2 + 1 y 2 + 9 z 2 = 1 z ≥ 1
There is a magnetic vector potential A = ( A x , A y , A z ) = ( 2 y + z , x 2 z , x y + z ) . What is the absolute value of the magnetic flux through the surface?
∫ ∫ B ⋅ d S = ?
The answer is 11.17.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Steven Chase
Please check last 4hr notifications
If you have read my last comment, then please reply.
@Steven Chase
sir how do you solve this transformer problems.
I am not able to solve that anaylitically .
Can we use python??
Log in to reply
Yeah, I don't recommend solving by hand. Using a computer program is much more convenient
Log in to reply
@Steven Chase
Yeah
But I don't know how to do that.
Can you little bit guide me??
(
The way you help me every day, I can't express it in words.
)
Thanks in advance
Log in to reply
@A Former Brilliant Member – The first thing to do is to re-write those two equations in a form that does not contain E 1 and E 2 . Those voltages should instead be written in terms of other quantities. Then you can manipulate those equations to solve for the currents. And then you can solve for E 2 . You can use Python to do numerical calculations with complex numbers. For example to make Z = 5 + j 1 0 in Python you can say Z = complex(5.0,10.0). And then those complex numbers can be used just like regular numbers.
Log in to reply
@Steven Chase
–
@Steven Chase
How to remove
E
1
and
E
2
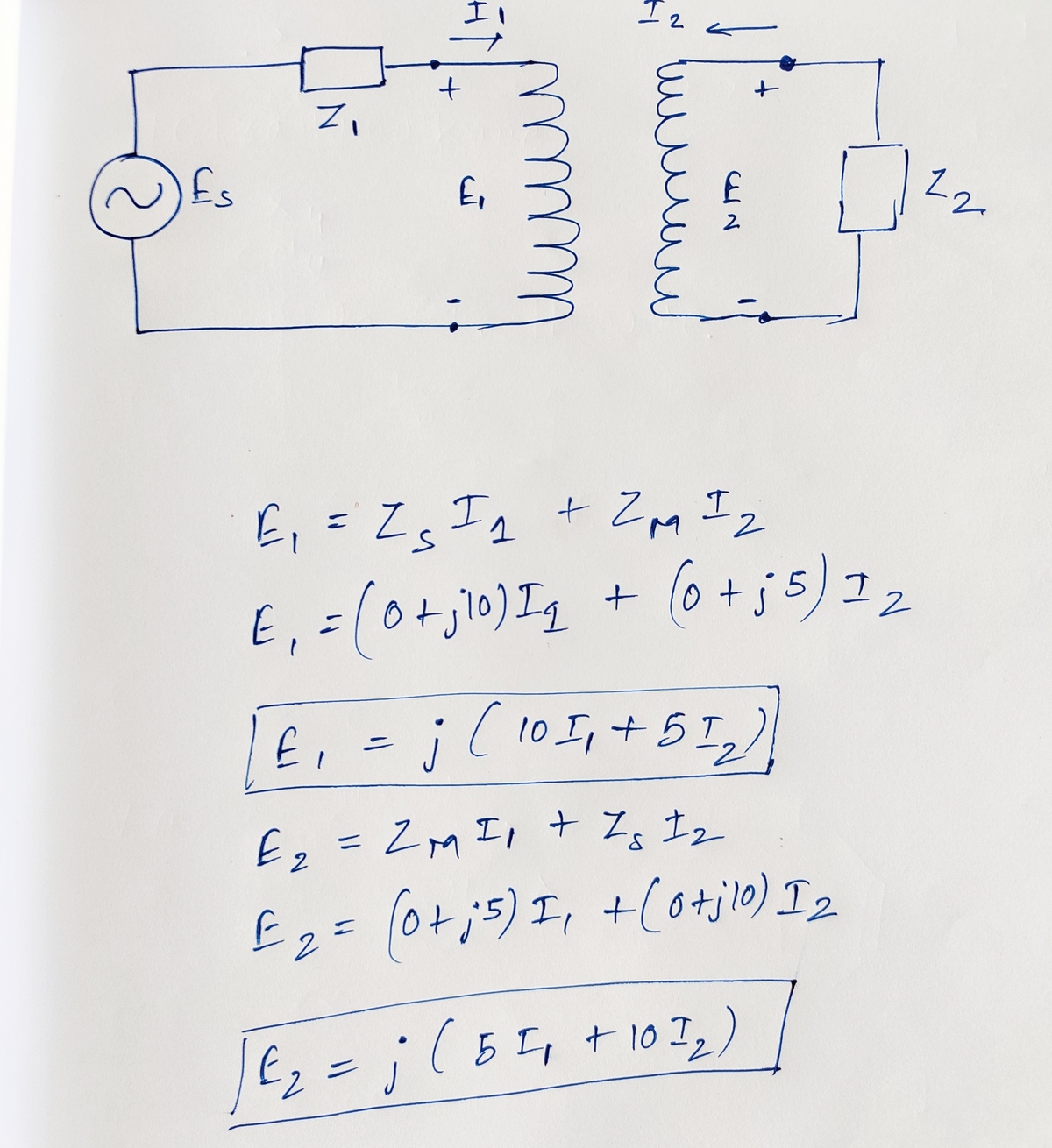
Log in to reply
@A Former Brilliant Member – Express them in terms of other quantities
Log in to reply
@Steven Chase – @Steven Chase sir is E 1 and E s same??
Log in to reply
@A Former Brilliant Member – No, they are not
Log in to reply
@Steven Chase
–
@Steven Chase
please tell me next step after my page work.
And what's the use of
E
s
Thanks in advance .
Hope I am not disturbing you.
Log in to reply
@A Former Brilliant Member – You can use Ohm's law
Log in to reply
@Steven Chase
–
@Steven Chase my only 1 try is left now .
I don't know what mistake I have done, here below I have attached my solution.

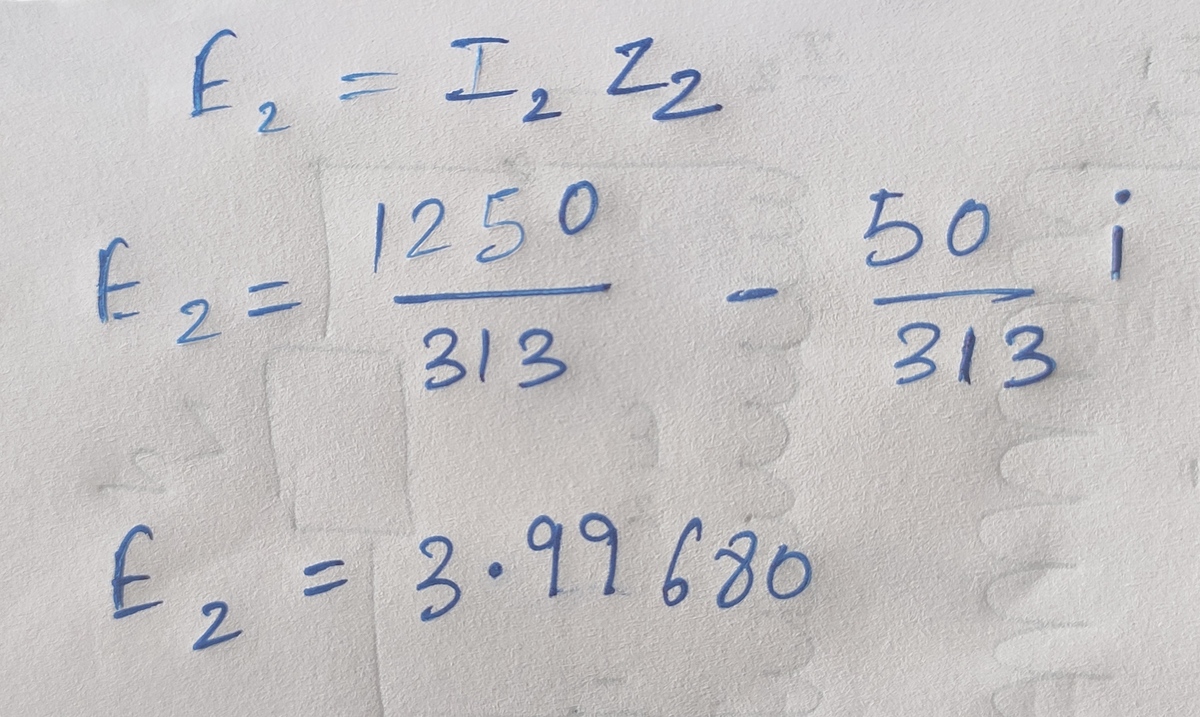
Log in to reply
@A Former Brilliant Member – Your relationship for E 1 is correct. And for E 2 , E 2 = − I 2 Z 2 . You were missing a negative sign.
Log in to reply
@Steven Chase
–
@Steven Chase
sir is the answer
≈
1
.
6
2
8
.
??
I am asking because I don't want to take risk.
Because I want to upload solution.
As always and obvious
(
Thanks in advance
)
Log in to reply
@A Former Brilliant Member – Yep, that's it. Nice job
Log in to reply
@Steven Chase
–
@Steven Chase
sir this question is very easy,
You may laugh at the above line because that I am only not able to solve and saying it easy.
Anyway but doing analytically it is not very hard.
Right??
Log in to reply
@A Former Brilliant Member – The conceptual aspects are the only ones worth spending time on, in my opinion. I don't see any reason to do calculations by hand.
Log in to reply
@Steven Chase
–
@Steven Chase
sir for calculating magnitude and solving equation I have also used Wolfram alpha.
Ok, sir no I am posting my solution and you post your solution using python
Because I want to learn from your solution.
Thanks in advance.
@Steven Chase
–
@Steven Chase
Sir did you woke up??
Are you posting part 3.
Thanks in advance.
Try to solve for the currents. Then once you have the currents, you can solve your first four equations (1-4) for the terminal voltages. Equations 5 and 6 get you part of the way toward solving for the currents. But you need a bit more.
Log in to reply
@Steven Chase
I think i need 2 more equations ,right??
And the formula for active power is
P
=
R
V
2
But how to apply that in this case
Log in to reply
Yes, you need two more equations. And the active power calculation is a bit more complex than that
Log in to reply
@Steven Chase – @Steven Chase is this the formula P = V I cos ϕ ??
@Steven Chase
Good Morning
suggest me a good book for Electrical Engineering.
I just want to solve and learn new things.
Thanks in advance.
@Steven Chase
I was trying your new problem to solve analytically.
I get
y
¨
+
y
2
=
0
Which is a second order non-linear differential equation.
Wolfram is not able to solve that, can Laplace solve this equation???
Should I use python?? Give your advice
Log in to reply
Use the best tool for the job
Log in to reply
@Steven Chase So what is the best tool for the job?? Obviously Python .
But the problem with me is that I didn't know that how to use python in these problems.
Log in to reply
@A Former Brilliant Member – The code can be similar to this:
https://brilliant.org/discussions/thread/kinematics-from-numerical-integration/?ref_id=1594302
@Steven Chase
sir today I am feeling very bad and depressed because I can't able to solve the below problem in my physics online test.
How will you approach these problem. The problem has to be solved with pen only. No tools.

Log in to reply
Do you know what the answers are supposed to be? I'm getting 5.89 amps through the capacitor and 2.53 volts at point A with respect to point C
Log in to reply
@Steven Chase
yes your both are correct .
Here you see
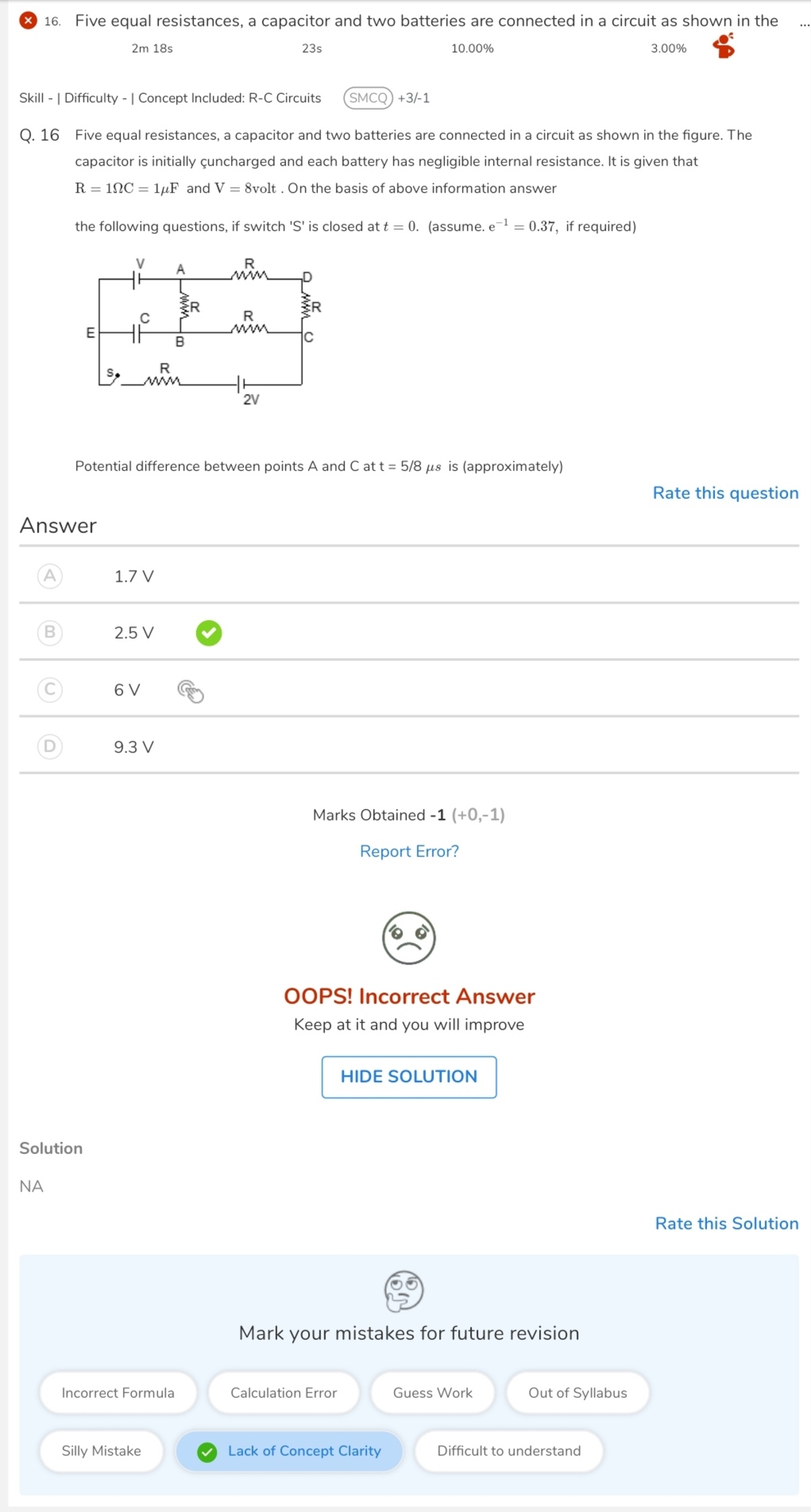
Can you please send me the solution.
The boundary curve of the given surface is:
4 x 2 + y 2 + 9 1 = 1
⟹ 4 x 2 + y 2 = 9 8
The curve can be parameterised as such:
r = 9 3 2 cos t i ^ + 9 8 sin t j ^ + k ^
⟹ d r = ( − 9 3 2 sin t i ^ + 9 8 cos t j ^ + 0 k ^ ) d t
The magnetic flux through the surface is (Using Stoke's theorem):
∫ S B ⋅ d S = ∫ S ( ∇ × A ) ⋅ d S = ∮ C A ⋅ d r
Here,
A = ( 2 y + z ) i ^ + x 2 z j ^ + ( x y + z ) k ^ ⟹ A = ( 2 y ( t ) + 1 ) i ^ + x ( t ) 2 j ^ + ( x ( t ) y ( t ) + 1 ) k ^
The required integrand is, therefore, after simplification:
d Φ = ⎝ ⎛ 2 7 6 4 2 cos ( t ) 3 − 3 4 2 sin ( t ) ( 3 4 2 sin ( t ) + 1 ) ⎠ ⎞ d t
Φ = ∫ 0 2 π ⎝ ⎛ 2 7 6 4 2 cos ( t ) 3 − 3 4 2 sin ( t ) ( 3 4 2 sin ( t ) + 1 ) ⎠ ⎞ d t Φ = − 9 3 2 π
@Karan Chatrath help me in the below problem
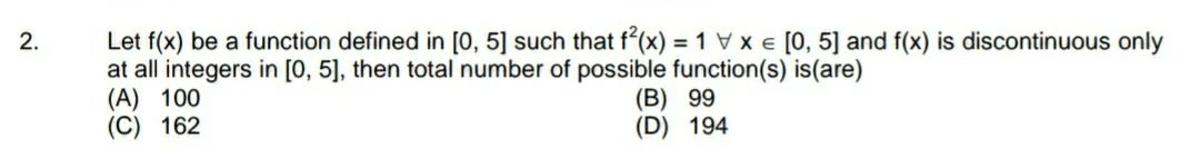 Thanks in advance
Thanks in advance
Log in to reply
To me, this seems like a collection of five binary switches, with two states each (negative one and positive one). So 2 5 = 3 2 . But that's not one of the options.
There are three ways to do this one:
1) Integrate B over the given surface
2) Integrate B over some other surface with the same boundary curve as the given surface
3) Integrate A over the boundary curve
The given surface is too complicated to deal with conveniently, so we can integrate over the interior of the flat ellipse at height z = 1 to accomplish procedure ( 2 ) . It is also convenient to implement procedure ( 3 ) . The first segment of the attached code implements procedure ( 2 ) , and the second segment of code implements procedure ( 3 ) .