Double Integrals ?
Calculate the total electric flux through the paraboloid surface due to a constant horizontal electric field of magnitude E .
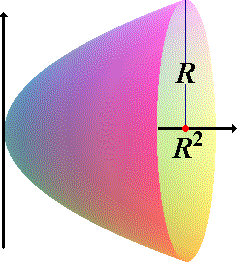
The radius of paraboloid is 2 m and height is 1 m .
E = 1 0 SI Units .
You need to calculate the electric flux only due to parabolic surface not due to base.
Give absolute value of flux
Take Horizontal direction along the axis of paraboloid (Line joining Top and base of paraboloid.
The answer is 125.663.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Exactly ! by the way there is no need to put modulus as electric field lines are going out of curved surface hence flux would be positive but i will still add as i think the orientation of paraboloid should be opposite to arrive at a positive answer. i dont understand your first line "Since electric field is constant". so if electric field is not constant then will charge be enclosed by paraboloid?
Log in to reply
If the electric field is not constant and in particular, if it has a non-zero divergence at a point then there is a non-zero charge density at a point. As an example, consider the following non-constant horizontal electric field in some region of space E ( x , y , z ) = x i ^ Then by the first Maxwell's equation (or equivalently Gauss' law in differential form) it follows that we have a constant positive charge density everywhere in that region.
Actually, I would like to mention that the problem has got nothing to do with Gauss' law or Electrodynamics and is purely a consequence of Divergence theorem . Since the divergence of the constant field is zero, its flux computed over any solid, closed body is zero. This explains the first line of my solution.
though i got it correct but please mention horizontal direction .
Log in to reply
i had mentioned it when i had posted it in the morning
Log in to reply
@Prakhar Bindal – i mean which one is horizontal.
Log in to reply
@Aryan Goyat – is it alright now?
Log in to reply
@Prakhar Bindal – yes, you can make part 2 taking the other line as direction of E.
Log in to reply
@Aryan Goyat – Thanks for your idea. currently i am quite busy as our centre has gone mad and they have started 5 days a week classes :(
Log in to reply
@Prakhar Bindal – ok, but please post it when you get out of your hectic schedule.
Log in to reply
@Aryan Goyat – and better ask only for the half part .
2 methods :
Easy method : Φ n e t = 0 ; Φ c i r c u l a r = − π E 0 R 2 ( inward flux) hence we simply obtain Φ c u r v e d = π E 0 R 2 .
Tough method : Focus on a differential area dA like in this figure
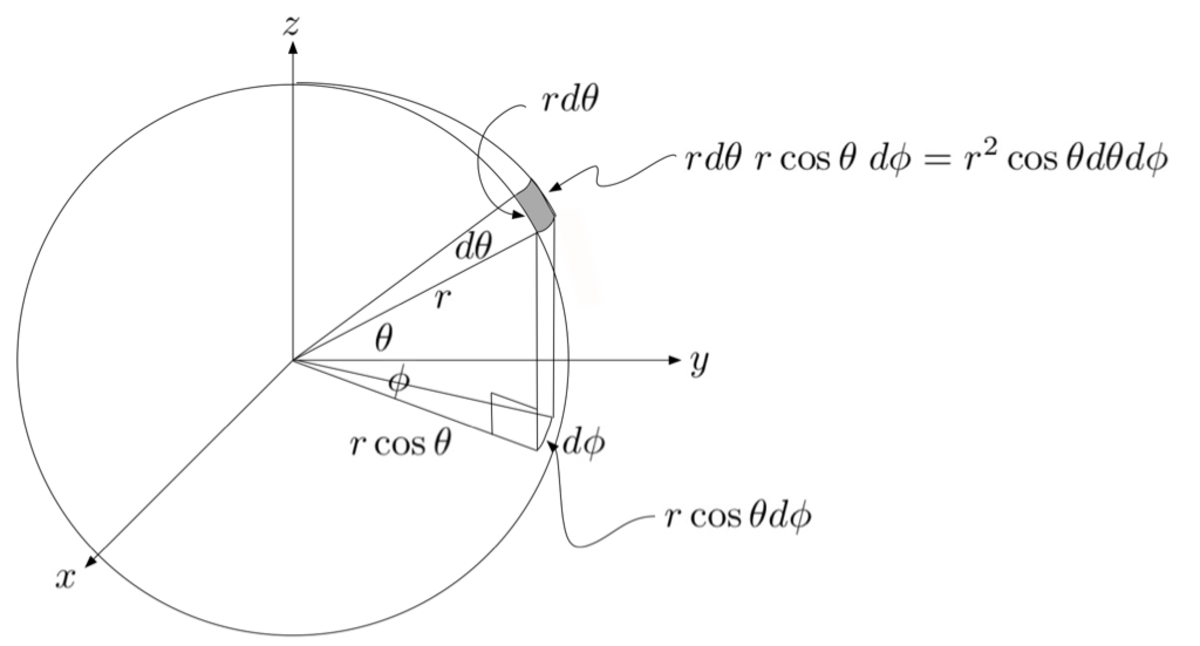
clearly
d A = r 2 c o s θ d θ d ϕ ; For simplicity lets assume E = a z ^ .
The normal vector is resolved as
r ^ = s i n θ z ^ + c o s θ s i n ϕ x ^ + c o s θ c o s ϕ y ^
Now using Gauss Law
Φ E : = ∮ E ⋅ r d A clearly E ⋅ r = E 0 s i n θ
So now we need ∫ ∫ E 0 s i n θ R 2 c o s θ d θ d ϕ
θ ∈ [ 0 , 2 π ] and ϕ ∈ [ 0 , 2 π ] so that
∫ 0 π / 2 ∫ 0 2 π E 0 R 2 s i n θ c o s θ d θ d ϕ = 2 π E 0 R 2 ∫ 0 π / 2 s i n θ c o s θ d θ = π E 0 R 2
Cant we simply say that the area of the projection of the area of the paraboloid = area of the base
⟹ E × 2 π R 2
Log in to reply
Log in to reply
@Md Zuhair Yea we can but at that time I had just learned the double integral method so just was showing off :P.
I'd look at sir @Abhishek Sinha's solution, 'cause it is so much simpler. But, if we want hard work, the flux Φ is defined by
Φ = ∫ ∫ R F ⋅ ⟨ − f x , − f y , 1 ⟩ d A ,
where R is the region we're considering, F is our vector field and f defines the surface. It is easy to notice that a possible choice for F and f is
F = E ⟨ 0 , 0 , 1 ⟩ ; f ( x , y ) = 4 x 2 + y 2 ,
where the region R must be a circle of radius 2 . Therefore
Φ = ∫ ∫ R E ⟨ 0 , 0 , 1 ⟩ ⋅ ⟨ − x / 2 , − y / 2 , 1 ⟩ d A = E ∫ ∫ R d A = 4 π E ≈ 1 2 5 . 6 6 3 Vm .
Since the Electric field is constant, there is no charge enclosed by the solid paraboloid body. Hence by Gauss' law, the total flux computed over the entire body is zero, i.e., ϕ curved surface + ϕ base = 0 Thus, ϕ curved surface = − ϕ base The right hand side of the equation is readily computed to be ϕ base = π R 2 E Thus, ∣ ϕ curved surface ∣ = π R 2 E